
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила вычисления абсолютной погрешности.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Таблица погрешностей косвенных измерений для наиболее употребляемых функций.
Запись результата измерений имеет вид: При этом необходимо соблюдать следующие правила: - погрешность DC округляется до двух значащих цифр, если первая из них 1 или 2, а во всех остальных случаях до одной значащей цифры, - число знаков после запятой в погрешности и в результате должно совпадать (позицию округления результата определяет величина абсолютной погрешности), -порядок величины, как правило, выносится за скобки. Например, u=(1,23±0,17)×103 м/с. Международная система единиц – СИ
Множители и приставки СИ для образования десятичных, кратных и дольных единиц
Лабораторная работа № 1 НЕУПРУГИЙ УДАР Цель работы: ознакомиться с практическим применением закона сохранения импульса на примере определения скорости одного из тел при неупругом ударе.
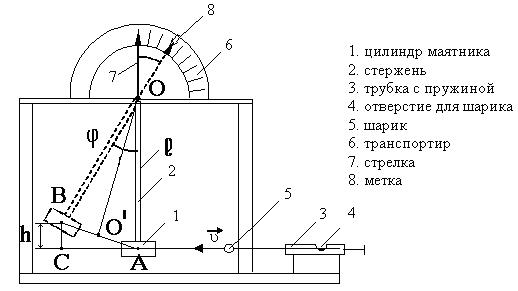
Приборы и принадлежности: баллистический маятник, шарик. Схема экспериментальной установки:
Методика исследования и описание установки При ударе происходит изменение на конечные значения скоростей тел за очень короткий промежуток времени. При этом между сталкивающимися телами возникают кратковременные ударные силы, превосходящие во много раз все внешние силы, действующие на них. Поэтому такую систему соударяющихся тел в процессе удара можно рассматривать практически как замкнутую и применять для нее закон сохранения импульса. Если после столкновения тела движутся как одно целое, т.е. с одной и той же скоростью, то такой удар называют неупругим. Примером указанного взаимодействия является соударение шарика массой m и начальной скоростью
На основании закона сохранения импульса имеем:
где В результате столкновения маятник придет в движение и отклонится на угол j, при этом кинетическая энергия переходит в потенциальную энергию и на основании закона сохранения энергии можно записать следующее уравнение:
где h – максимальная высота поднятия центра тяжести маятника. Отсюда
Из подобия треугольников ABC и OBO’ (рис.1) следует
Но
Решая совместно выражения (1),(3),(4), получим уравнение для определения начальной скорости шарика:
Для определения скорости тела - шарика, вызывающего смещение маятника из первоначального состояния покоя, используется установка, схема которой приведена на рисунке. Установка состоит из массивного цилиндра 1, подвешенного на практически нерастяжимом стержне 2. Внутри цилиндра 1 имеется углубление, заполненное пластилином. На некотором расстоянии от него по оси расположена трубка 3, внутри которой размещена пружина. В трубке сверху имеется отверстие 4, предназначенное для опускания внутрь нее шарика 5. При этом пружина должна быть в сжатом состоянии. После нажатия на спусковое устройство 6 пружина выбрасывает шарик из трубки с некоторой скоростью
Порядок выполнения работы 1. По указанию преподавателя откройте программу, содержащую блок лабораторных работ по физике, раздел «механика, статистическая физика и термодинамика». Выберите нужную вам лабораторную работу. 2. Еще раз внимательно прочитайте теорию и методику проведения работы. Для этого щелкните левой клавишей мыши на экране кнопку «Теория и методика проведения работы». 3. Откройте flash - анимацию, для этого щелкните кнопку «Эксперимент». 4. По указанию преподавателя задайте данные для коэффициента жесткости k, x, m, l, M и щелкните ОК. 5. С помощью мыши оттяните пружину пистолета и отпустите ее. 6. Запишите значения М, m, l, j в таблицу. 7. Повторите опыт 10 раз, каждый раз записывая полученные значения в таблицу. 8. Произведите вычисления предлагаемых величин. 9. Сделайте вывод о проделанной работе. 10. Ответьте на контрольные вопросы.
Обработка результатов измерений 1. Смещение центра тяжести маятника определить по формуле
2. Начальная скорость шарика определяется по формуле (5). 3. Расчет относительной погрешности провести по формуле
4. Расчет абсолютной погрешности провести по формуле
где Δ M, Δ m, Δ l, Δj, Δg – абсолютные погрешности измерения соответственно массы маятника и шарика, расстояния от точки подвеса до центра тяжести маятника, угла отклонения маятника и ускорения свободного падения.
Таблица измерений:
Контрольные вопросы: 1. Что понимают под ударом? Дайте определение абсолютно упруго и неупругого удара. 2. Дайте определение импульса тела. 3. Сформулируйте закон сохранения импульса. 4. Запишите закон сохранения импульса для данной установки. 5. Можно ли считать, что кинетическая энергия шарика, в случае неупругого удара полностью переходит в потенциальную энергию маятника? 6. Запишите формулу для определения изменения кинетической энергии системы двух сталкивающихся тел при абсолютно неупругом, прямом центральном ударе.
Лабораторная работа №2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.141 (0.011 с.) |

 , где Хmax-верхний предел измерений прибора;
-если класс точности К на панели прибора заключен в кружок:
, где Хmax-верхний предел измерений прибора;
-если класс точности К на панели прибора заключен в кружок:  , где Х-показание прибора.
, где Х-показание прибора.
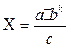 .
Рабочую формулу логарифмируют:
.
Рабочую формулу логарифмируют:  Затем дифференцируют:
Затем дифференцируют:
 .
Переходят от бесконечно малых к конечным и заменяют - на +, т.е.
.
Переходят от бесконечно малых к конечным и заменяют - на +, т.е.
 Окончательно получаем,
Окончательно получаем,
 .
.
 , затем рассчитывается погрешность каждого измерения
, затем рассчитывается погрешность каждого измерения  .
.



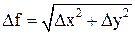




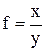


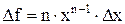

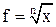








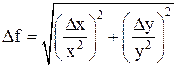
 .
.
 с баллистическим маятником, в углублении цилиндра которого на месте контакта помещается слой неупругого материала - пластилина. При столкновении таких тел шарик застревает в пластилине и маятник вместе с ним движется как одно целое. При ударе происходит изменение на конечные значения скоростей тел за очень короткий промежуток времени. При этом между сталкивающимися телами возникают кратковременные ударные силы, превосходящие во много раз все внешние силы, действующие на них. Поэтому такую систему соударяющихся тел в процессе удара можно рассматривать практически как замкнутую и применять для нее закон сохранения импульса. Если после столкновения тела движутся как одно целое, т.е. с одной и той же скоростью, то такой удар называют неупругим.
с баллистическим маятником, в углублении цилиндра которого на месте контакта помещается слой неупругого материала - пластилина. При столкновении таких тел шарик застревает в пластилине и маятник вместе с ним движется как одно целое. При ударе происходит изменение на конечные значения скоростей тел за очень короткий промежуток времени. При этом между сталкивающимися телами возникают кратковременные ударные силы, превосходящие во много раз все внешние силы, действующие на них. Поэтому такую систему соударяющихся тел в процессе удара можно рассматривать практически как замкнутую и применять для нее закон сохранения импульса. Если после столкновения тела движутся как одно целое, т.е. с одной и той же скоростью, то такой удар называют неупругим. , (1)
, (1)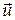 - скорость цилиндра маятника с шариком после удара; M – масса маятника; m – масса груза;
- скорость цилиндра маятника с шариком после удара; M – масса маятника; m – масса груза;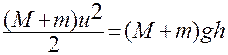 , (2)
, (2) . (3)
. (3) .
.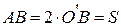 , т.е. равно смещению центра тяжести маятника, а OB=ℓ - расстоянию от точки подвеса до центра тяжести маятника. Поэтому для определения h получаем следующее выражение:
, т.е. равно смещению центра тяжести маятника, а OB=ℓ - расстоянию от точки подвеса до центра тяжести маятника. Поэтому для определения h получаем следующее выражение: . (4)
. (4) . (5)
. (5) . (6)
. (6) . (7)
. (7) , (8)
, (8)


