
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признак Лейбница. Абсолютная и условная сходимость рядаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема (признак Лейбница). Знакочередующийся ряд сходится, если: 1) последовательность абсолютных величин членов ряда монотонно убывает, т.е. 2) общий член ряда стремится к нулю: Пусть дан знакопеременный ряд Пример 1. Исследовать на сходимость ряд Итак, исходный ряд не является абсолютно сходящимся. 2. Выясним, сходится ли данный знакочередующийся ряд, применяя признак Лейбница. · Проверим, выполняется ли неравенство величин членов данного ряда:
Данное неравенство эквивалентно неравенству · Найдём предел общего члена ряда: Таким образом, для данного знакочередующегося ряда выполнены оба условия, содержащиеся в признаке Лейбница, откуда следует, что исходный ряд сходится, однако он не является абсолютно сходящимся, поэтому данный ряд сходится условно. Ответ: ряд Задание 6. Исследовать на абсолютную и условную сходимость ряды:
Функциональные ряды Понятие функционального ряда Ряд, членами которого являются функции от x, называется функциональным:
Степенные ряды Степенным рядом называется ряд вида:
Областью сходимости степенного ряда называется множество всех значений Число R называется радиусом сходимости степенного ряда, если при
т.е. если степенной ряд сходится при любых Если Сходимость степенного ряда при Пример 2. Найти область сходимости ряда. Решение. Найдём радиус сходимости ряда:
Следовательно, ряд сходится при При
Ответы: Задание 1. 1) 8) Задание 2. 1) да, 2) да, 3) да, 4) нет, 5) нет, 6) да, 7) да, 8) нет, 9) нет, 10) да. Задание 3. 1)сходится, 2) расходится, 3) расходится, 4) расходится, 5) сходится, 6) сходится, 7) расходится, 8) расходится, 9) сходится, 10) сходится. Задание 4. 1) расходится, 2) сходится, 3) сходится, 4) сходится, 5) сходится, 6) сходится, 7) сходится, 8) расходится, 9) сходится, 10) расходится. Задание 5. 1) расходится, 2) сходится, 3) сходится, 4) расходится, 5) сходится, 6) расходится, 7) сходится, 8) расходится, 9) расходится, 10) расходится. Задание 6. 1) абсолютно сходится, 2) условно сходится, 3) условно сходится, 4) условно сходится, 5) абсолютно сходится, 6) абсолютно сходится, 7) абсолютно сходится, 8) абсолютно сходится, 9) условно сходится, 10) условно сходится. Задание 7. 1) (-2;2], 2)
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 910; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.009 с.) |

 .
. . При этом сумма S ряда удовлетворяет неравенствам
. При этом сумма S ряда удовлетворяет неравенствам 
 , где
, где  – произвольные числа (действительные или комплексные). Если ряд
– произвольные числа (действительные или комплексные). Если ряд  , составленный из абсолютных величин его членов, сходится, то данный ряд
, составленный из абсолютных величин его членов, сходится, то данный ряд  также сходится. В этом случае знакопеременный ряд
также сходится. В этом случае знакопеременный ряд  называется абсолютно сходящимся. Следовательно, если же знакопеременный ряд
называется абсолютно сходящимся. Следовательно, если же знакопеременный ряд  сходится, а ряд
сходится, а ряд  расходится, то данный ряд
расходится, то данный ряд 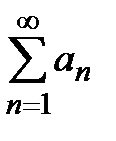 называется условно сходящимся.
называется условно сходящимся. Решение. 1. Исследуем на сходимость ряд
Решение. 1. Исследуем на сходимость ряд  из абсолютных величин членов данного ряда:
из абсолютных величин членов данного ряда: 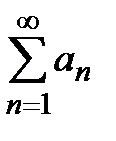 =
= 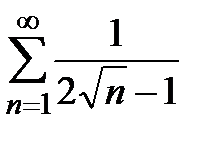 .Сравним этот ряд с рядом
.Сравним этот ряд с рядом  . Так как
. Так как  <
<  , то
, то  >
>  для всех n. Ряд
для всех n. Ряд  расходится, так как расходится ряд
расходится, так как расходится ряд  (как ряд Дирихле
(как ряд Дирихле  при p=
при p=  <1). Значит, по 1-му признаку сравнения расходится и ряд
<1). Значит, по 1-му признаку сравнения расходится и ряд  .
.  >
>  для абсолютных
для абсолютных =
=  >
>  .
. <
<  , которое верно для любого n=1,2….Значит
, которое верно для любого n=1,2….Значит  для все номеров n = 1,2…
для все номеров n = 1,2… =
=  = 0.
= 0.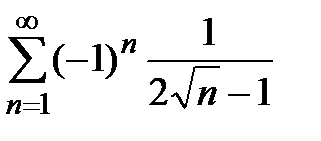 сходится условно.
сходится условно.




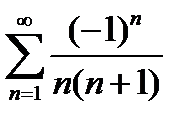




 Придавая
Придавая  определенное значение
определенное значение  , получим числовой ряд
, получим числовой ряд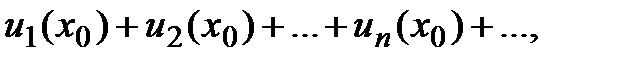 который может быть как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка
который может быть как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка  называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда. Совокупность числовых значений аргумента x, при которых функциональный ряд сходится, называется его областью сходимости. В области сходимости функционального ряда его сумма является некоторой функцией от
называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда. Совокупность числовых значений аргумента x, при которых функциональный ряд сходится, называется его областью сходимости. В области сходимости функционального ряда его сумма является некоторой функцией от  :
:  . Определяется она в области сходимости равенством
. Определяется она в области сходимости равенством  , где
, где  частичная сумма ряда.
частичная сумма ряда.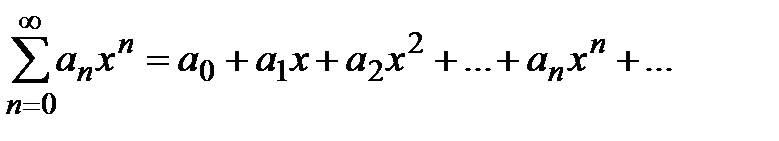 .
. , при которых данный ряд сходится.
, при которых данный ряд сходится. ряд сходится и притом абсолютно, а при
ряд сходится и притом абсолютно, а при 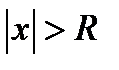 ряд расходится. Радиус сходимости найдем, используя признак Даламбера:
ряд расходится. Радиус сходимости найдем, используя признак Даламбера:
 , удовлетворяющих данному условию и расходится при
, удовлетворяющих данному условию и расходится при  . Отсюда следует, что если существует предел
. Отсюда следует, что если существует предел  ,то радиус сходимости ряда
,то радиус сходимости ряда  равен этому пределу и степенной ряд сходится при
равен этому пределу и степенной ряд сходится при 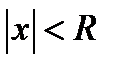 , т.е. в промежутке
, т.е. в промежутке  , который называется промежутком (интервалом) сходимости.
, который называется промежутком (интервалом) сходимости.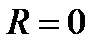 , то степенной ряд сходится в единственной точке
, то степенной ряд сходится в единственной точке 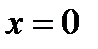 . На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.
. На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться. и
и  исследуется с помощью какого-либо из признаков сходимости.
исследуется с помощью какого-либо из признаков сходимости.
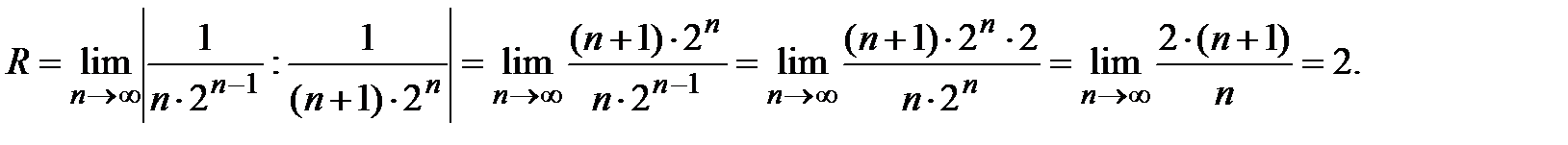
 , т.е. при
, т.е. при  . При
. При  имеем ряд
имеем ряд  , который сходится по признаку Лейбница.
, который сходится по признаку Лейбница. имеем расходящийся ряд:
имеем расходящийся ряд: 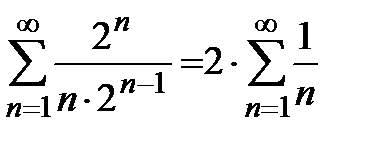 . Ответ: областью сходимости исходного ряда является промежуток
. Ответ: областью сходимости исходного ряда является промежуток  Задание 7. Найти область сходимости степенного ряда:
Задание 7. Найти область сходимости степенного ряда: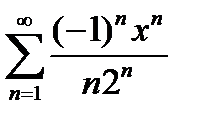





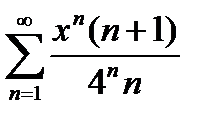

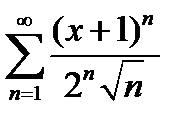
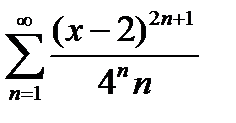
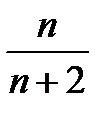 , 2)
, 2)  , 3)
, 3)  , 4), 5)
, 4), 5) 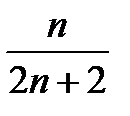 , 6)
, 6)  , 7)
, 7)  ,
,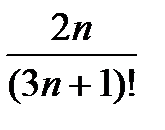 , 9)
, 9) 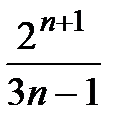 , 10)
, 10) 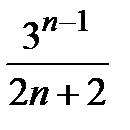 .
. , 3)
, 3) 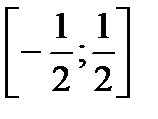 , 4) (-4;4), 5) [-3;1), 6) [-1;5], 7) (-6;2), 8) (-2;1), 9)
, 4) (-4;4), 5) [-3;1), 6) [-1;5], 7) (-6;2), 8) (-2;1), 9) 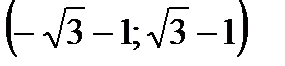 , 10) (0;4).
, 10) (0;4).


