
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная и условная сходимости рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знакочередующийся ряд является частным случаем знакопеременного ряда. Определение 2.2. Числовой ряд
Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.
Теорема 2.2. Пусть дан знакопеременный ряд
Если сходится ряд, составленный из модулей членов данного ряда
то сходится и сам знакопеременный ряд (2.2).
Надо отметить, что обратное утверждение неверно: если сходится ряд (2.2), то это не означает, что будет сходиться ряд (2.3).
Определение 2.3. Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место. Такие ряды обладают рядом свойств, которые сформулируем без доказательства.
Произведение двух абсолютно сходящихся рядов с суммами Таким образом, абсолютно сходящиеся ряды суммируются, вычитаются, перемножаются как обычные ряды. Суммы таких рядов не зависит от порядка записи членов.
В случае условно сходящихся рядов соответствующие утверждения (свойства), вообще говоря, не имеют места. Так, переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда измениться. Например, ряд
Сумма уменьшилась вдвое! Более того, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд (теорема Римана).
Поэтому действия над рядами нельзя производить, не убедившись в их абсолютной сходимости. Для установления абсолютной сходимости используют все признаки сходимости числовых рядов с положительными членами, заменяя всюду общий член его модулем.
Пример 2.1. Исследовать на сходимость ряд Решение. Исходный ряд знакопеременный. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда, т.е. ряд Пример 2.2. Исследовать на сходимость ряд Решение. 1) Данный ряд знакочередующийся. Используем признак Лейбница. Проверим, выполняются ли условия.
Следовательно, исходный ряд сходится. 2) Рассмотрим ряд, составленный из абсолютных членов
По признаку Даламбера ряд, составленный из абсолютных членов, сходится. Значит, исходный знакочередующийся ряд сходится абсолютно., Пример 2.3. Исследовать на сходимость ряд Решение. 1) Данный ряд знакочередующийся. Используем признак Лейбница. Проверим, выполняются ли условия.
Следовательно, исходный ряд сходится. 2) Рассмотрим ряд, составленный из абсолютных членов
Следовательно, оба ряда ведут себя одинаково, т.е. ряд, составленный из абсолютных членов, тоже расходится. Значит, исходный знакочередующийся ряд сходится условно., Пример 2.4. Исследовать на сходимость ряд Решение. Данный ряд знакочередующийся. Используем признак Лейбница. Проверим, выполняются ли условия.
Следовательно, исходный ряд расходится. , Пример 2.5. Вычислить сумму ряда Решение. Данный ряд знакочередующийся. По признаку Лейбница этот ряд является сходящимся. Значит, величина отброшенного при вычислении остатка ряда, который также является знакочередующимся рядом, не превосходит первого отброшенного члена (на основании следствия из признака Лейбница).
Нужное число членов
, 3. ФУНКЦИОНАЛЬНЫЕ И СТЕПЕННЫЕ РЯДЫ
Функциональные ряды
Определение 3.1. Пусть функции
называется функциональным рядом.
Придавая
который может быть как сходящимся, так и расходящимся. Определение 3.2. Если числовой ряд
Область сходимости функционального ряда обозначим Пример 3.1. Найти область сходимости функционального ряда
Решение. Область определения функций – это Данный ряд является членом геометрической прогрессии со знаменателем
Поэтому область сходимости исследуемого ряда является интервал , Так как каждому
где В таком случае
Пример 3.2. Найти область сходимости и сумму функционального ряда
Решение. Данный ряд является рядом геометрической прогрессии со знаменателем В области сходимости данного функционального ряда найдем сумму. По формуле суммы геометрической прогрессии при
,
Степенные ряды
Среди функциональных рядов в математике и ее приложениях особую роль играют ряды, членами которых являются степенные функции аргумента Определение 3.3. Степенным рядом называется функциональный ряд вида
где При
Ряд (3.2) легко приводится к ряду (3.3), если положить Выясним вопрос о сходимости степенного ряда (3.3). Область сходимости этого степенного ряда содержит, по крайней мере, одну точку Об области сходимости степенного ряда можно судить, исходя из следующей теоремы. Теорема 3.1 (теорема Абеля). Если степенной ряд (3.3) сходится в точке
Доказательство. Рассмотрим числовой ряд Запишем ряд (3.3) следующим образом:
и составим ряд из абсолютных членов
В силу установленного неравенство каждый член здесь меньше соответствующего члена геометрической прогрессии со знаменателем
Если , Несмотря на то, что
Следствие. Если степенной ряд (3.3) расходится в точке
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.104.73 (0.011 с.) |

 , члены которого после любого номера
, члены которого после любого номера  имеют разные знаки, называется знакопеременным.
имеют разные знаки, называется знакопеременным. . (2.2)
. (2.2) , (2.3)
, (2.3)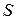 , то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму
, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму  и
и  можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна
можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна  (или соответственно
(или соответственно  ).
). и
и  понимается ряд вида:
понимается ряд вида:
 .
. условно сходится по признаку Лейбница. Пусть сумма этого ряда равна
условно сходится по признаку Лейбница. Пусть сумма этого ряда равна 
 .
. . Так как
. Так как  , то члены сходного ряда не больше членов ряда Дирихле
, то члены сходного ряда не больше членов ряда Дирихле  , который, как известно, сходится. Следовательно, на основании признака сравнения данный ряд сходится абсолютно.,
, который, как известно, сходится. Следовательно, на основании признака сравнения данный ряд сходится абсолютно., .
. - выполняется;
- выполняется; - выполняется.
- выполняется. . Исследуем его на сходимость, используя признак Даламбера
. Исследуем его на сходимость, используя признак Даламбера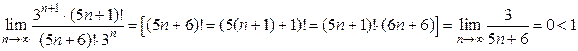 .
. .
. - выполняется;
- выполняется; - выполняется.
- выполняется. . Исследуем его на сходимость, используя предельный признак сравнения. Рассмотрим гармонический ряд
. Исследуем его на сходимость, используя предельный признак сравнения. Рассмотрим гармонический ряд  , который расходится.
, который расходится. .
. .
. - выполняется;
- выполняется; - не выполняется.
- не выполняется. с точностью
с точностью  .
. найдем путем подбора из неравенства
найдем путем подбора из неравенства  . При
. При  последнее неравенство выполняется, значит, если отбросить в данном ряде все члены, начиная с шестого, то требуемая точность будет обеспечена. Следовательно,
последнее неравенство выполняется, значит, если отбросить в данном ряде все члены, начиная с шестого, то требуемая точность будет обеспечена. Следовательно,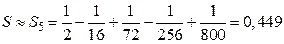 .
. определены в области
определены в области  . Тогда выражение вида
. Тогда выражение вида (3.1)
(3.1)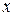 определенные значения
определенные значения  , получаем числовой ряд
, получаем числовой ряд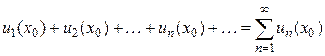 ,
, сходится при
сходится при  , то ряд называется сходящимся в точке
, то ряд называется сходящимся в точке  . Как правило, область
. Как правило, область  .
. .
. .
. . Такой ряд сходится, если
. Такой ряд сходится, если  .
. Û
Û  Û
Û  .
. . Таким образом,
. Таким образом,  соответствует некоторое число – сумма числового ряда, то указанное соответствие определяет функцию
соответствует некоторое число – сумма числового ряда, то указанное соответствие определяет функцию  , которая называется суммой ряда (3.1) в области
, которая называется суммой ряда (3.1) в области  ,
, -
-  - есть
- есть  .
. .
. . Следовательно, этот ряд сходится при
. Следовательно, этот ряд сходится при  , т.е. при всех
, т.е. при всех  . Таким образом, область сходимости
. Таким образом, область сходимости  .
. получаем
получаем , при
, при  , (3.2)
, (3.2) - постоянные числа, называемые коэффициентами ряда,
- постоянные числа, называемые коэффициентами ряда,  получаем степенной ряд вида
получаем степенной ряд вида . (3.3)
. (3.3) . Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (3.3).
. Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (3.3). (ряд (3.2) сходится в точке
(ряд (3.2) сходится в точке  , то он абсолютно сходится при всех
, то он абсолютно сходится при всех  .
. , который сходится по условию. Следовательно, по необходимому признаку сходимости
, который сходится по условию. Следовательно, по необходимому признаку сходимости  . Поэтому все члены ряда ограничены в своей совокупности, т.е. существует такое постоянное положительное число
. Поэтому все члены ряда ограничены в своей совокупности, т.е. существует такое постоянное положительное число  , что при всех
, что при всех 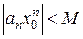 .
. ,
, .
. :
: .
. и прогрессия сходится. Поэтому сходится и ряд, составленный из абсолютных величин. А значит, абсолютно сходится ряд (3.3).
и прогрессия сходится. Поэтому сходится и ряд, составленный из абсолютных величин. А значит, абсолютно сходится ряд (3.3). , мы не можем сразу воспользоваться признаком сравнения, поскольку в условии теоремы не сказано, что ряд в самой точке
, мы не можем сразу воспользоваться признаком сравнения, поскольку в условии теоремы не сказано, что ряд в самой точке 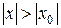 .
.


