
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимый признак сходимости рядаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Г Л А В А 11 РЯДЫ ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. Пусть дана последовательность действительных чисел Выражение вида
называется числовым рядом, числа Если для последовательности Ряд (1.1) называется расходящимся, если
Ряд сходится или расходится вместе со своим остатком. НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА Теорема 1. Если ряд (1.1) сходится, то его общий член стремится к нулю:
Следствие. Если Пример. Исследовать сходимость ряда Ñ Найдем: Пример. Исследовать сходимость гармонического ряда
Ñ Очевидно, условие (2.1) выполняется: ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ЧИСЛОВЫМИ РЯДАМИ. ПРОСТЕЙШИЕ СВОЙСТВА ЧИСЛОВЫХ РЯДОВ Рассмотрим ряды:
Ряд (с) называется суммой рядов (а) и (b), а ряд (d) – произведением ряда (а) на число a. Если сходятся ряды (а) и (b), то сходятся и ряды (с) и (d) и если ЗНАКОПОЛОЖИТЕЛЬНЫЕ РЯДЫ Ряд
Приведем некоторые достаточные признаки сходимости знакоположительных рядов. Теорема 2. (признак сравнения в непредельной форме). Даны 2 ряда
Если, начиная с некоторого n, выполняется условие Теорема 3. (признак сравнения в предельной форме). Даны 2 ряда:
Если существует конечный и не равный нулю предел: В качестве рядов для сравнения удобно выбирать: 1) гармонический ряд
Признак сравнения в предельной форме особенно эффективен для рядов, общий член которых есть алгебраическая функция целого аргумента, либо функция, в пределе приводимая к вышеуказанной (использование таблицы эквивалентных бесконечно малых), т.к. позволяет свести исследование сходимости исходного ряда к рассмотрению одного из трех “эталонных” рядов. Пример. Исследовать сходимость ряда
Ñ Ряд знакоположительный, применим к нему признак сравнения в предельной форме, сравнив его с рядом
Пример. Исследовать сходимость ряда Ñ Ряд знакоположительный. Т.к. при Пример. Исследовать на сходимость ряд Ñ Ряд дан знакоположительный. Т.к. Теорема 4. (признак Даламбера). Дан ряд
Если существует Признак Даламбера не дает результата для рядов с общим членом в виде дробно-рациональной функции или функции, содержащей под радикалом переменную n, т.к. замена n на n +1 не меняет коэффициента при старших степенях n. Признак эффективен в случае наличия в общем члене ряда показательной функции или факториалов. Заметим, что n!=1×2×3… n. Пример. Исследовать сходимость ряда
c помощью признака Даламбера. Ñ Здесь Тогда
Пример. Исследовать сходимость ряда Ñ Теорема 5 (признак Коши, радикальный). Дан ряд (4.1). Если существует Радикальный признак Коши дает результат в случае, когда общий член ряда имеет вид степенно-показательной функции целочисленного аргумента. Пример. Исследовать сходимость ряда Ñ Ряд знакоположительный, применим к нему признак Коши; найдем
Теорема 6 (интегральный признак Коши). Дан ряд (4.1). Если функция y = f (x) удовлетворяет следующим условиям: 1) Интегральный признак Коши удобно применять в тех случаях, когда функция f (x), полученная заменой в общем члене ряда целочисленной переменной n на непрерывную переменную x, обладает легко находимой первообразной. Пример. Исследовать сходимость ряда Ñ Рассмотрим функцию
Рассмотрим несобственный интеграл
Найдем отдельно Здесь для нахождения предела применили правило Лопиталя. Далее: ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ Ряд называется знакочередующимся, если он имеет вид
Теорема 7 (признак Лейбница). Если члены знакочередующегося ряда не возрастают по абсолютной величине с ростом n, т.е., начиная с некоторого n, верно неравенство Пример. Исследовать сходимость ряда Ñ Ряд знакочередующийся. Применим признак Лейбница (теорема 7).
Пример. Исследовать сходимость ряда Ñ Дан знакочередующийся ряд. Члены этого ряда по абсолютной величине монотонно убывают. В самом деле, ЗНАКОПЕРЕМЕННЫЕ РЯДЫ Ряд Теорема 8 (признак абсолютной сходимости). Дан ряд Ряд Т.к. знакочередующийся ряд – частный случай знакопеременного ряда, то и к знакочередующемуся ряду можно применять признак абсолютной сходимости. Пример. Исследовать сходимость ряда ÑДан знакопеременный ряд. Применим к нему признак абсолютной сходимости. Составим ряд из абсолютных величин членов исходного ряда:
Если ряд Пример. Исследовать на абсолютную или условную сходимость так называемый ряд Лейбница
Ñ По признаку Лейбница (теорема 7) этот ряд сходится, т.к. для него выполняются оба условия этого признака: a) б) Теорема 9. В сходящемся (абсолютно или условно) ряде можно группировать члены, не меняя их порядка. Иными словами, если сходится ряд Теорема 10. Абсолютно сходящийся ряд остается сходящимся и сохраняет сумму при любой перестановке его членов. Теорема11. В условно сходящемся ряде при соответствующей перестановке его членов можно сделать его сумму равной любому наперед заданному числу или сделать ряд расходящимся. Произведением рядов
Теорема 12. Если перемножаемые ряды сходятся абсолютно, то ряд - произведение сходится также абсолютно и имеет сумму, равную Краткие рекомендации по применению тех или иных признаков сходимости к соответствующим рядам приведены в нижеследующей таблице.
Следует иметь в виду, что существуют и другие признаки сходимости рядов, с которыми можно познакомиться в литературе, указанной к этому задачнику. Задачи для самостоятельного решения Найти сумму ряда, исходя из определения. 1. Доказать расходимость рядов с помощью необходимого признака. 4. Решить вопрос о сходимости рядов с помощью признаков сравнения. 7. 10. 13. Исследовать сходимость рядов с помощью признака Даламбера. 15. 18. Исследовать сходимость рядов с помощью признака Коши (радикального). 21. Исследовать сходимость рядов с помощью интегрального признака Коши. 24. Выяснить, какие из рядов сходятся, какие расходятся. 26. 29. 31. 34. Исследовать сходимость следующих рядов. В случае сходимости исследовать, как ряды сходятся: абсолютно или условно. 36. 39. 42. 45.
46. Показать, что если ряды 47. Показать, что если ряд 48. Дан ряд 49. Сколько нужно взять членов ряда Ответы к задачам главы 11
34) Сходится 36) Сходится абсолютно 37) Сходится условно 38) Сходится абсолютно 39) Сходится абсолютно 40) Расходится 41) Сходится условно 42) Сходится условно 43) Расходится 44) Сходится абсолютно 45) Сходится абсолютно 48) а) ошибка по модулю меньше 49) а) 99членов; б) 999 членов. Г Л А В А 12 ФУНЦИОНАЛЬНЫЕ РЯДЫ ФУНКЦИОНАЛЬНЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ Ряд
членами которого являются функции от x, определенные на множестве D, называется функциональным рядом. Если числовой ряд
Для нахождения области сходимости ряда (1.1) можно использовать эталонные ряды и достаточные признаки сходимости числовых рядов. Пример. Найти область сходимости ряда Ñ Данный ряд представляет собой обобщенный гармонический ряд, который сходится при Пример. Найти область сходимости ряда Ñ Данный ряд является геометрической прогрессией, которая сходится, если Пример. Найти область сходимости ряда
Ñ Для нахождения области сходимости данного ряда используем признак Даламбера, который применим лишь к рядам с положительными членами. Составим ряд из абсолютных величин членов данного ряда:
и к нему применим признак Даламбера (теорема 11.4). Задачи для самостоятельного решения Найти область сходимости следующих рядов. 1.
6. 11. 15. 18.
ТЕЙЛОРА И МАКЛОРЕНА Пусть функция
называется рядом Тейлора для функции f (x). Если же для всех значений x из некоторой окрестности т.
то f (x) называется разложимой в ряд Тейлора в окрестности т.
и называется рядом Маклорена. Теорема 8. Для того, чтобы функция
Теорема 9. Если То же самое в символической записи:
При разложении 1) Непосредственное разложение 2) Использование готовых разложений:
Пример. Разложить Ñ Решим эту задачу двумя способами. I способ. Используем непосредственное разложение функции в ряд Тейлора:1)
……………………………………………………
…………………………………………………… Вычислим найденные производные в т. x = 2:
Составим формально ряд Тейлора:
б) Найдем область сходимости ряда (5.2), используя признак Даламбера:
Этот результат будет справедлив при любых x, следовательно, ряд (5.2) сходится на всей числовой оси: в) Докажем, что при всех x ряд (5.2) сходится к
II способ. Разложим
В ряд Маклорена для cos x
справа и слева вместо x подставим
(т.к. в (5/3) При разложении функции в ряд часто используют почленное дифференцирование и интегрирование рядов. Пример. Разложить в ряд Маклорена Ñ Предварительно разложим в ряд Маклорена функцию
Поэтому
Задачи для самостоятельного решения Следующие функции разложить в ряд Маклорена 33. 39. 44. Следующие функции разложить в ряд Тейлора в окрестности т. Указать область сходимости найденного ряда к своей сумме. 48. 52. 55. ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ Если некоторое число S разложено в ряд
и то поправка на отбрасывание всех остальных членов выразится остатком
Как произвести оценку погрешности? 1)Если ряд (6.1) – знакочередующийся, то остаток D имеет знак своего первого члена 2) Если ряд (6.1) – знакоположительный, то остаток D оценивают либо с помощью остаточного члена формулы Тейлора, либо пытаются найти легко суммируемый тоже знакоположительный ряд, члены которого были бы больше членов инт
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 811; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.232 (0.011 с.) |


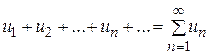 (1.1)
(1.1)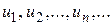 - членами ряда,
- членами ряда,  - n -ым или общим членом ряда. Сумма n первых членов ряда называется n -ой частичной суммой и обозначается символом
- n -ым или общим членом ряда. Сумма n первых членов ряда называется n -ой частичной суммой и обозначается символом  :
:  .
. частичных сумм существует конечный предел S, то ряд (1.1) называется сходящимся, а число S – суммой данного ряда. В этом случае пишут:
частичных сумм существует конечный предел S, то ряд (1.1) называется сходящимся, а число S – суммой данного ряда. В этом случае пишут:  ;
;  .
. не существует или бесконечен. Ряд, полученный из (1.1) отбрасыванием первых его m членов, называется остатком ряда (1.1):
не существует или бесконечен. Ряд, полученный из (1.1) отбрасыванием первых его m членов, называется остатком ряда (1.1):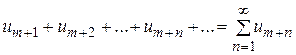 (1.2)
(1.2)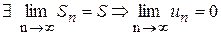 (2.1)
(2.1) , то ряд (1.1) расходится.
, то ряд (1.1) расходится. .
. (в числителе стоит показательная функция, которая растет быстрее, чем n), следовательно, ряд расходится. #
(в числителе стоит показательная функция, которая растет быстрее, чем n), следовательно, ряд расходится. #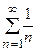 . (2.2)
. (2.2) , однако, гармонический ряд расходится. Действительно, если предположить, что ряд (2.2) сходится и его сумма равна S, то
, однако, гармонический ряд расходится. Действительно, если предположить, что ряд (2.2) сходится и его сумма равна S, то  . Тогда из неравенства
. Тогда из неравенства  Þ
Þ  . Получили противоречие. #
. Получили противоречие. #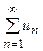 ;
;  ;
;  ;
;  . (3.1 a,b,c,d)
. (3.1 a,b,c,d)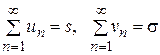 , то
, то 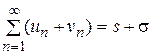 ;
;  .
.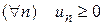 . (4.1)
. (4.1) и
и  . (4.2 a, b)
. (4.2 a, b) и ряд (b) сходится, то сходится и ряд (а). Если же ряд (а) расходится, то ряд (b) тоже расходится.
и ряд (b) сходится, то сходится и ряд (а). Если же ряд (а) расходится, то ряд (b) тоже расходится.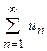 и
и  , то ряды (а) и (b) сходятся или расходятся одновременно.
, то ряды (а) и (b) сходятся или расходятся одновременно. , который расходится; 2) обобщенный гармонический ряд
, который расходится; 2) обобщенный гармонический ряд 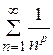 (ряд Дирихле), который сходится при p >1 и расходится при p £1; 3) геометрическую прогрессию
(ряд Дирихле), который сходится при p >1 и расходится при p £1; 3) геометрическую прогрессию  , которая сходится, если
, которая сходится, если 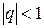 и расходится, если
и расходится, если  .
. .
. , который сходится как обобщенный гармонический ряд с
, который сходится как обобщенный гармонический ряд с  .
. 
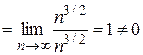 . Предел отношения общих членов этих рядов при
. Предел отношения общих членов этих рядов при  конечный, не равный нулю, следовательно, ряды ведут себя одинаково; данный ряд сходится. Ряд для сравнения подбираем следующим образом: при
конечный, не равный нулю, следовательно, ряды ведут себя одинаково; данный ряд сходится. Ряд для сравнения подбираем следующим образом: при 
 ;
;  #
# .
. , то
, то  , поэтому для сравнения берем ряд
, поэтому для сравнения берем ряд  . Последний ряд является гармоническим, все члены которого умножены на
. Последний ряд является гармоническим, все члены которого умножены на  , что не влияет на его расходимость. Т.к.
, что не влияет на его расходимость. Т.к.  и ряд
и ряд  расходится, то
расходится, то  .
.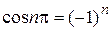 , т.е. он может быть равен 1 или–1, то
, т.е. он может быть равен 1 или–1, то 
 . Из последнего неравенства видно, что исходный ряд можно сравнить с рядом
. Из последнего неравенства видно, что исходный ряд можно сравнить с рядом  , а этот ряд сходится (обобщенный гармонический с p =2>1, все члены которого умножены на 4). Но т.к. ряд
, а этот ряд сходится (обобщенный гармонический с p =2>1, все члены которого умножены на 4). Но т.к. ряд  , то при q <1 ряд сходится, при q >1 ряд расходится; при q =1 вопрос о сходимости ряда остается открытым.
, то при q <1 ряд сходится, при q >1 ряд расходится; при q =1 вопрос о сходимости ряда остается открытым.
 .
.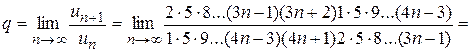
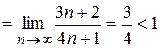 . Ряд сходится, т.к. q <1. #
. Ряд сходится, т.к. q <1. # .
. ,
,  =
= 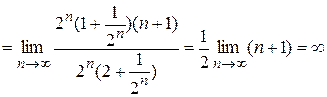 . Т.к. q >1, ряд расходится. #
. Т.к. q >1, ряд расходится. #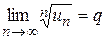 , то при q <1 ряд сходится; при q >1 ряд расходится; при q =1 вопрос о сходимости ряд остается открытым.
, то при q <1 ряд сходится; при q >1 ряд расходится; при q =1 вопрос о сходимости ряд остается открытым. .
. .По теореме 5 ряд сходится. #
.По теореме 5 ряд сходится. # ; 2) непрерывна, положительна и монотонно убывает при
; 2) непрерывна, положительна и монотонно убывает при  , то ряд (4.1) и несобственный интеграл
, то ряд (4.1) и несобственный интеграл  одновременно сходятся или расходятся.
одновременно сходятся или расходятся. .
. . При натуральных значениях аргумента значения функции совпадают с соответствующими членами ряда:
. При натуральных значениях аргумента значения функции совпадают с соответствующими членами ряда: 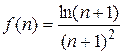 . Кроме того, f (x) при
. Кроме того, f (x) при  будет непрерывной, положительной и монотонно убывающей (функция
будет непрерывной, положительной и монотонно убывающей (функция  , стоящая в знаменателе, растет быстрее, чем ln(x +1), стоящая в числителе). Показать, что f (x) будет монотонно убывающей, можно и с помощью
, стоящая в знаменателе, растет быстрее, чем ln(x +1), стоящая в числителе). Показать, что f (x) будет монотонно убывающей, можно и с помощью  :
:


 для
для  , следовательно, f (x) - убывающая на [1,+¥).
, следовательно, f (x) - убывающая на [1,+¥). , который берется по частям:
, который берется по частям:
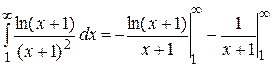 .
. .
. . Итак,
. Итак,  . Интеграл сходится, следовательно, сходится и данный ряд. #
. Интеграл сходится, следовательно, сходится и данный ряд. # (5.1)
(5.1)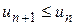 и
и  , то ряд (5.1) сходится, причем, если его сумма равна s, то
, то ряд (5.1) сходится, причем, если его сумма равна s, то 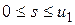 .
. .
. ,
, . Очевидно, что
. Очевидно, что 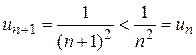 . Кроме того,
. Кроме того, 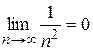 . Выполнены оба условия признака Лейбница, следовательно, ряд сходится. #
. Выполнены оба условия признака Лейбница, следовательно, ряд сходится. # .
. , т.к.
, т.к. 
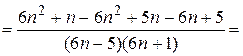
 . Однако,
. Однако, 
 . Значит, ряд расходится по необходимому признаку (теорема 1, следствие), по признаку Лейбница расходимость не установить. #
. Значит, ряд расходится по необходимому признаку (теорема 1, следствие), по признаку Лейбница расходимость не установить. # .
. . Если сходится ряд
. Если сходится ряд  , то сходится и ряд
, то сходится и ряд  .
. . Этот знакоположительный ряд сравним в непредельной форме с рядом
. Этот знакоположительный ряд сравним в непредельной форме с рядом  , который представляет собой геометрическую прогрессию с
, который представляет собой геометрическую прогрессию с  , следовательно,
, следовательно, 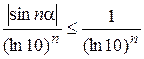 , тогда ряд
, тогда ряд  расходится, то ряд
расходится, то ряд  (6.1)
(6.1) и
и . Но ряд, составленный из абсолютных величин данного ряда,
. Но ряд, составленный из абсолютных величин данного ряда,  является гармоническим, который расходится (см. 2.2). Следовательно, ряд Лейбница сходится условно. #
является гармоническим, который расходится (см. 2.2). Следовательно, ряд Лейбница сходится условно. #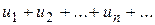 , то сходится и ряд
, то сходится и ряд 
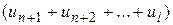 +
+  , причем оба ряда имеют одну и ту же сумму.
, причем оба ряда имеют одну и ту же сумму.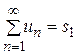 и
и  называется ряд
называется ряд  , где
, где
 .
. 2.
2.  3.
3. 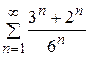
 5.
5.  6.
6. 
 8.
8.  9.
9. 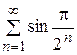
 11.
11. 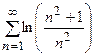 12.
12. 
 14.
14. 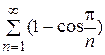
 16.
16.  17.
17. 
 19.
19.  20.
20. 
 22.
22.  23.
23. 
 25.
25. 
 27.
27.  28.
28. 
 30.
30. 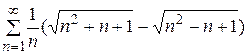
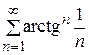 32.
32.  33.
33. 
 35. Доказать, что
35. Доказать, что  .
.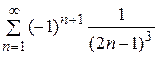 37.
37.  38.
38. 
 40.
40.  41.
41. 
 43.
43.  44.
44. 
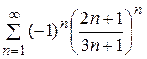
 и
и  сходятся, то и ряд
сходятся, то и ряд 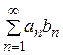 абсолютно сходится.
абсолютно сходится. абсолютно сходится, то и ряд
абсолютно сходится, то и ряд  тоже абсолютно сходится.
тоже абсолютно сходится. Оценить ошибку, допускаемую при замене суммы этого ряда суммой его первых четырех членов. Суммой первых пяти членов. Что можно сказать о знаке этих ошибок?
Оценить ошибку, допускаемую при замене суммы этого ряда суммой его первых четырех членов. Суммой первых пяти членов. Что можно сказать о знаке этих ошибок? , чтобы вычислить его сумму с точностью до 0,01? до 0,001?
, чтобы вычислить его сумму с точностью до 0,01? до 0,001?


 , ошибка отрицательная.
, ошибка отрицательная.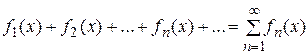 , (1.1)
, (1.1) сходится, где
сходится, где  , то
, то  называется точкой сходимости ряда (1.1). Множество всех точек сходимости ряда (1.1) называется областью сходимости ряда (1.1). Если существует
называется точкой сходимости ряда (1.1). Множество всех точек сходимости ряда (1.1) называется областью сходимости ряда (1.1). Если существует  , где
, где 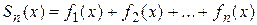 ,
, 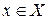 , то говорят, что ряд (1.1) сходится на множестве X к S (x). S (x) называется суммой ряда (1.1). На языке “
, то говорят, что ряд (1.1) сходится на множестве X к S (x). S (x) называется суммой ряда (1.1). На языке “  ” это можно записать так:
” это можно записать так:
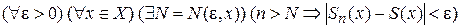 .
.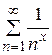 .
. и расходится при
и расходится при  . Областью сходимости ряда является интервал
. Областью сходимости ряда является интервал  .#
.# .
. .
.  . Область сходимости ряда – интервал
. Область сходимости ряда – интервал  .#
.# (a)
(a)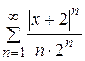 (б)
(б)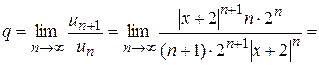
 . Ряд (б) будет сходиться, если
. Ряд (б) будет сходиться, если 
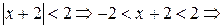
 . Тогда ряд (а) будет сходиться, и притом абсолютно в интервале (-4, 0). При
. Тогда ряд (а) будет сходиться, и притом абсолютно в интервале (-4, 0). При 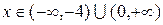 ряд (а) расходится, как не удовлетворяющий необходимому признаку сходимости
ряд (а) расходится, как не удовлетворяющий необходимому признаку сходимости  (следствие из теоремы (11.1)). Если
(следствие из теоремы (11.1)). Если  , то ответа о сходимости ряда признак Даламбера не дает и при
, то ответа о сходимости ряда признак Даламбера не дает и при  и
и 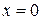 ряд нужно исследовать особо. При
ряд нужно исследовать особо. При 
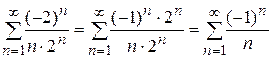 , который сходится (ряд Лейбница) (см. задачу раздела (11.6)). При
, который сходится (ряд Лейбница) (см. задачу раздела (11.6)). При  - гармонический ряд, который расходится (раздел 11.2). Итак, областью сходимости ряда (а) будет промежуток [-4,0). #
- гармонический ряд, который расходится (раздел 11.2). Итак, областью сходимости ряда (а) будет промежуток [-4,0). # . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
. . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10. 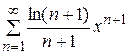 .
. . 12.
. 12.  . 13.
. 13.  . 14.
. 14. 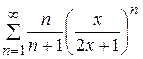 .
. . 16.
. 16. 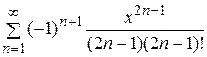 . 17.
. 17.  .
. . 19.
. 19. 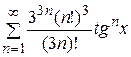 .
. имеет в т.
имеет в т. 
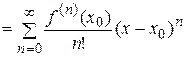 (5.1)
(5.1)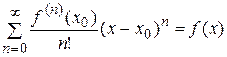 ,
, ). Если x = 0, то ряд Тейлора имеет вид
). Если x = 0, то ряд Тейлора имеет вид
 .
. - остаточный член формулы Тейлора. Записанный в форме Лагранжа, он имеет вид:
- остаточный член формулы Тейлора. Записанный в форме Лагранжа, он имеет вид:  ,
, 

 имеет в некотором промежутке, содержащем т.
имеет в некотором промежутке, содержащем т.  , то
, то 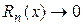 при
при 
 .
. для любых n, вычисляют
для любых n, вычисляют  и подставляют найденные значения в (5.1); b) находят область сходимости ряда (5.1); c) выясняют, для каких значений x из области сходимости ряда
и подставляют найденные значения в (5.1); b) находят область сходимости ряда (5.1); c) выясняют, для каких значений x из области сходимости ряда  .
.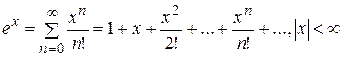


 .
.
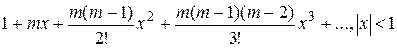
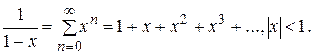
 в ряд Тейлора в окрестности т. x = 2.
в ряд Тейлора в окрестности т. x = 2.
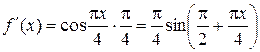 ;
;

 …,
…, ,…
,…
 (5.2)
(5.2)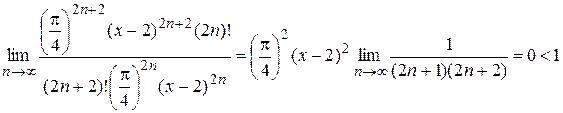
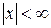 .
.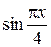 , для чего достаточно показать, что
, для чего достаточно показать, что 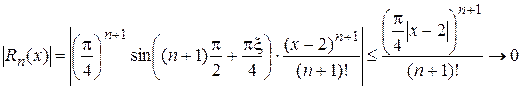 при
при  . Как результат решения задачи можем записать:
. Как результат решения задачи можем записать: ,
,  .
.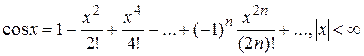 (5.3)
(5.3) , получим:
, получим:
 ; (5.4)
; (5.4) #
# .
. , для чего в разложении
, для чего в разложении  заменим x на
заменим x на  .
.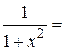

 .
.



 (получившийся ряд сходится и в граничных точках). #
(получившийся ряд сходится и в граничных точках). # ; 34.
; 34.  35.
35.  ; 36.
; 36.  ; 37.
; 37.  ; 38.
; 38.  ;
; ; 40.
; 40. 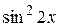 . 41.
. 41. 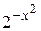 ; 42.
; 42.  ; 43.
; 43.  .
.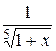 ; 45.
; 45. 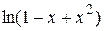 ; 46.
; 46.  ; 47.
; 47. 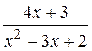 .
. . 49.
. 49.  . 50.
. 50.  . 51.
. 51.  .
.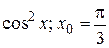 . 53.
. 53.  . 54.
. 54.  .
. . 56.
. 56.  .
.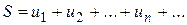 (6.1)
(6.1) ,
, .
. и
и  .
.


