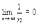60. Знакочередующиеся ряды. Теорема Лейбница.
Знакочередующийся ряд. Рассмотрим ряд  и распишем его подробнее: и распишем его подробнее: 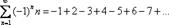 . У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности. Знакочередование обеспечивает множитель . У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности. Знакочередование обеспечивает множитель  : если : если  чётное, то будет знак «плюс», если нечётное – знак «минус». Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн». В практических примерах знакочередование членов ряда может обеспечивать не только множитель чётное, то будет знак «плюс», если нечётное – знак «минус». Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн». В практических примерах знакочередование членов ряда может обеспечивать не только множитель 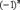 , но и подобные ему: , но и подобные ему:  , , 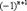 , ,  , …. Например: , …. Например: 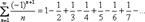 . Подводным камнем являются «обманки»: . Подводным камнем являются «обманки»: 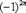 , , 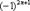 , ,  и т.п. – такие множители не обеспечивают смену знака. Чтобы исследовать знакочередующийся ряд на сходимость необходимо использовать признак Лейбница.
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится. Или в два пункта: 1) Ряд является знакочередующимся. 2) Члены ряда убывают по модулю: и т.п. – такие множители не обеспечивают смену знака. Чтобы исследовать знакочередующийся ряд на сходимость необходимо использовать признак Лейбница.
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится. Или в два пункта: 1) Ряд является знакочередующимся. 2) Члены ряда убывают по модулю:  . Причём, убывают монотонно. Если выполнены оба условия, то ряд сходится.
61. Знакопеременные ряды. Мажорирующие ряды. Условная и абсолютная сходимости рядов.
Знакопеременный ряд. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.
Мажорирующий ряд. Числовой ряд . Причём, убывают монотонно. Если выполнены оба условия, то ряд сходится.
61. Знакопеременные ряды. Мажорирующие ряды. Условная и абсолютная сходимости рядов.
Знакопеременный ряд. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.
Мажорирующий ряд. Числовой ряд 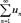 называется мажорирующим ряд называется мажорирующим ряд  , если для любого n выполняется неравенство , если для любого n выполняется неравенство  Абсолютная и условная сходимость.
Ряд
Абсолютная и условная сходимость.
Ряд 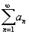 называется абсолютно сходящимся, если ряд называется абсолютно сходящимся, если ряд 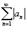 также сходится. Если ряд также сходится. Если ряд 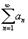 сходится абсолютно, то он является сходящимся (в обычном смысле).Обратное утверждение неверно. Ряд сходится абсолютно, то он является сходящимся (в обычном смысле).Обратное утверждение неверно. Ряд  называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
62. Функциональные ряды. Основные определения.
Определение 1. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: U1(x) + U2(x) + … + Un(x) + … (1)
Определение 2. Если при X = X0 ряд (1) сходится, то X0 называется точкой сходимости ряда (1).
Определение 3. Множество всех значений х, при которых функциональный ряд сходится, называется областью сходимости этого ряда. Очевидно, что в области сходимости функционального ряда его сумма является функцией от х. Она обозначается S(x).
Степенной ряд – наиболее популярная разновидность функционального ряда, это ряд, в общий член Un(x) которого входят целые положительные степени независимой переменной x. Упрощенно степенной ряд записывается так: называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
62. Функциональные ряды. Основные определения.
Определение 1. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: U1(x) + U2(x) + … + Un(x) + … (1)
Определение 2. Если при X = X0 ряд (1) сходится, то X0 называется точкой сходимости ряда (1).
Определение 3. Множество всех значений х, при которых функциональный ряд сходится, называется областью сходимости этого ряда. Очевидно, что в области сходимости функционального ряда его сумма является функцией от х. Она обозначается S(x).
Степенной ряд – наиболее популярная разновидность функционального ряда, это ряд, в общий член Un(x) которого входят целые положительные степени независимой переменной x. Упрощенно степенной ряд записывается так: 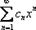 , где Cn – это многочлены, степени, факториалы, зависящие только от «эн». Простейший пример ряда: , где Cn – это многочлены, степени, факториалы, зависящие только от «эн». Простейший пример ряда: 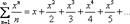 63. Теорема о непрерывности суммы функционального ряда.
Теорема. На любом отрезке целиком лежащем внутри интервала сходимости степенного ряда
63. Теорема о непрерывности суммы функционального ряда.
Теорема. На любом отрезке целиком лежащем внутри интервала сходимости степенного ряда  , сумма ряда есть непрерывная функция.
Доказательство. Каждая частичная сумма степенного ряда, очевидно, является непрерывной функцией. На любом отрезке целиком лежащем внутри интервала сходимости ряда сходимость является равномерной. Сумма ряда, являющаяся пределом равномерно сходящейся последовательности непрерывных функций, сама является непрерывной функцией. Теорема доказана.
64. Теоремы о почленном дифференцировании и интегрировании функциональных рядов.
Почленное интегрирование степенного ряда. Теорема. Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
Почленное дифференцирование степенного ряда. Теорема. Пусть степенной ряд , сумма ряда есть непрерывная функция.
Доказательство. Каждая частичная сумма степенного ряда, очевидно, является непрерывной функцией. На любом отрезке целиком лежащем внутри интервала сходимости ряда сходимость является равномерной. Сумма ряда, являющаяся пределом равномерно сходящейся последовательности непрерывных функций, сама является непрерывной функцией. Теорема доказана.
64. Теоремы о почленном дифференцировании и интегрировании функциональных рядов.
Почленное интегрирование степенного ряда. Теорема. Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
Почленное дифференцирование степенного ряда. Теорема. Пусть степенной ряд
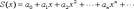 имеет радиус сходимости R. Тогда ряд имеет радиус сходимости R. Тогда ряд
 полученный в результате почленного дифференцирования ряда полученный в результате почленного дифференцирования ряда 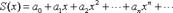 , также имеет радиус сходимости R. Производная суммы ряда , также имеет радиус сходимости R. Производная суммы ряда 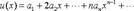 равна сумме ряда: равна сумме ряда: 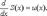 65. Степенные ряды Лемма.
Пусть r < R. Тогда
65. Степенные ряды Лемма.
Пусть r < R. Тогда 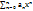 сходится на множестве |x| ≤ r абсолютно и равномерно.
Доказательство. Так как r < R, ряд сходится на множестве |x| ≤ r абсолютно и равномерно.
Доказательство. Так как r < R, ряд 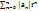 сходится. Так как | сходится. Так как | 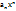 | ≤ | ≤ 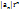 , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
66. 1-я и 2-я теоремы Абеля о сходимости степенного ряда. , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
66. 1-я и 2-я теоремы Абеля о сходимости степенного ряда.
 67. Аналитические функции и представление их степенным рядом.
Функция f называется аналитической в точке x0, если в некоторой окрестности этой точки она разлагается в степенной ряд:
67. Аналитические функции и представление их степенным рядом.
Функция f называется аналитической в точке x0, если в некоторой окрестности этой точки она разлагается в степенной ряд:  (1)
Естественной областью определения аналитической функции будет радиус сходимости ряда (1).
Пусть в окрестности точки (x0, y0, z0, q0) задана аналитическая функция f(x, y, z, q) своих 2n+2 переменных. Пусть далее w(y) – аналитическая функция в окрестности значения y0, и пусть z0 = w(y0), q0 = (grad w) y = y0
Тогда дифференциальное уравнение в достаточно малой окрестности точки (x0, y0) имеет ровно одно аналитическое решение z = ψ(x, y), которое при x = x0 принимает значение ψ(x0, y) = w(y). Коэффициенты степенного ряда для ψмогут быть получены применением к ψ обычного метода степенных рядов и приравниванием коэффициентов при соответствующих степенях с учетом начальных условий.
68. Ряды Фурье. Основные определения.
Говорят, что функция f(x) имеет период P, если f(x + P) = f(x) для всех значений x. Пусть период функции f(x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
1. Предположим, что функция f(x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле: (1)
Естественной областью определения аналитической функции будет радиус сходимости ряда (1).
Пусть в окрестности точки (x0, y0, z0, q0) задана аналитическая функция f(x, y, z, q) своих 2n+2 переменных. Пусть далее w(y) – аналитическая функция в окрестности значения y0, и пусть z0 = w(y0), q0 = (grad w) y = y0
Тогда дифференциальное уравнение в достаточно малой окрестности точки (x0, y0) имеет ровно одно аналитическое решение z = ψ(x, y), которое при x = x0 принимает значение ψ(x0, y) = w(y). Коэффициенты степенного ряда для ψмогут быть получены применением к ψ обычного метода степенных рядов и приравниванием коэффициентов при соответствующих степенях с учетом начальных условий.
68. Ряды Фурье. Основные определения.
Говорят, что функция f(x) имеет период P, если f(x + P) = f(x) для всех значений x. Пусть период функции f(x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
1. Предположим, что функция f(x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:
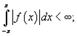 2. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции.
Определение 1. Последовательность функций фи1(х), фи2(х), фи3(х) называется нормированной на отрезке [a; b], если
2. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции.
Определение 1. Последовательность функций фи1(х), фи2(х), фи3(х) называется нормированной на отрезке [a; b], если
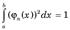 для всех n
Определение 2. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортогональной на отрезке [a; b], если для всех n
Определение 2. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортогональной на отрезке [a; b], если
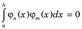 при при  Определение 3. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортонормальной на отрезке [a; b], если она является нормированной и ортогональной, т.е.
Определение 3. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортонормальной на отрезке [a; b], если она является нормированной и ортогональной, т.е.
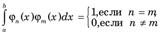 69. Коэффициенты ряда Фурье.
Коэффициенты Фурье функции f периода 2π:
69. Коэффициенты ряда Фурье.
Коэффициенты Фурье функции f периода 2π:
  или
или
 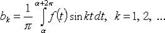 80. Интеграл Дюамеля
80. Интеграл Дюамеля
 81. Применение операционного исчисления
Задача Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами:
x ^(n) + a1 x^ (n - 1) + a2 x ^(n - 2) + … + a(n – 1) x ′ + an x = f (t),
x(0) = x0, x′ (0) = x1, x″ (0) = x2, …, x ^(n -1) (0) = x(n -1).
Начальные условия в этой задаче заданы в точке t0 = 0. Если начальные условия задаются в другой точке t0 ≠ 0, то заменой аргумента u = t - t0 их сдвигают в точку u0 = 0.
Метод решения этой задачи основан на теореме о дифференцировании оригинала. Предположим, что функция x(t), её производные до n-го порядка, правая часть f(t) являются функциями-оригиналами, и x(t) = X(p). Тогда
x ′(t) = p X(p) − x(0) = p X(p) − x0, x ″(t) = p2 X(p) − p x0− x1, …, x^(n)(t) = p^(n) X(p) − p ^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1), и изображение задачи будет иметь вид p^n X(p) − p^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1) +
+ a1(p^(n – 1) X(p) − p^(n – 2) x0 − p^(n – 3) x1 − … − x(n – 2)) + …
+a(n – 1) (p X(p) − x0) + a(n) X(p) = F(p), где F(p)= f (t) - изображение правой части уравнения. Это линейное относительно X(p) алгебраическое уравнение, решив которое, находим X(p). Оригинал этого изображения и будет решением задачи Коши.
Вычисление несобственных интегралов
Если f = F, g = G, то
81. Применение операционного исчисления
Задача Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами:
x ^(n) + a1 x^ (n - 1) + a2 x ^(n - 2) + … + a(n – 1) x ′ + an x = f (t),
x(0) = x0, x′ (0) = x1, x″ (0) = x2, …, x ^(n -1) (0) = x(n -1).
Начальные условия в этой задаче заданы в точке t0 = 0. Если начальные условия задаются в другой точке t0 ≠ 0, то заменой аргумента u = t - t0 их сдвигают в точку u0 = 0.
Метод решения этой задачи основан на теореме о дифференцировании оригинала. Предположим, что функция x(t), её производные до n-го порядка, правая часть f(t) являются функциями-оригиналами, и x(t) = X(p). Тогда
x ′(t) = p X(p) − x(0) = p X(p) − x0, x ″(t) = p2 X(p) − p x0− x1, …, x^(n)(t) = p^(n) X(p) − p ^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1), и изображение задачи будет иметь вид p^n X(p) − p^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1) +
+ a1(p^(n – 1) X(p) − p^(n – 2) x0 − p^(n – 3) x1 − … − x(n – 2)) + …
+a(n – 1) (p X(p) − x0) + a(n) X(p) = F(p), где F(p)= f (t) - изображение правой части уравнения. Это линейное относительно X(p) алгебраическое уравнение, решив которое, находим X(p). Оригинал этого изображения и будет решением задачи Коши.
Вычисление несобственных интегралов
Если f = F, g = G, то
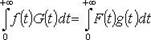 79. Свертка функций
79. Свертка функций
 Вариант из Интернета (возможно он будет получше):
Сверткой функций f1(t) и f2(t) называется функция
Вариант из Интернета (возможно он будет получше):
Сверткой функций f1(t) и f2(t) называется функция  Свёртка обозначается символом f1 * f2: Свёртка обозначается символом f1 * f2:
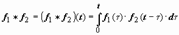 Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f1(t) и f2(t) не больше, чем на 1. Действительно, пусть Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f1(t) и f2(t) не больше, чем на 1. Действительно, пусть 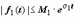 , , 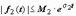 , ,
 , тогда , тогда 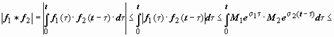
 , так как t < e^t. , так как t < e^t.
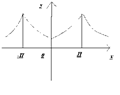
| 70. Ряд Фурье для четных функций.
Пусть f (x) - четная функция с периодом 2 L, удовлетворяющая условию f (- x) = f (x) .
Тогда для коэффициентов ее ряда Фурье находим формулы:
 = = 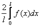
 = = 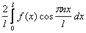
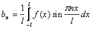 = 0 = 0  , где n =1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2 L выглядит так: , где n =1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2 L выглядит так:
 71. Ряд Фурье для нечетных функций
Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
71. Ряд Фурье для нечетных функций
Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
 где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так: где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
 Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
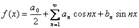 , где , где 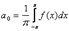 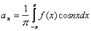 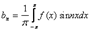 Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
72. Ряд Фурье для функций с периодом 2l
Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
72. Ряд Фурье для функций с периодом 2l
Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
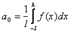 = = 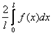 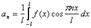 = = 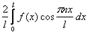 ; ;  = 0, где n=1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так: = 0, где n=1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:
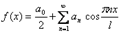 Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
 где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так: где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
 Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
 , где , где   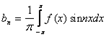 Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
73. Ряд Фурье для непериодических функций
Y = f(x) a <= x <=b
Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
73. Ряд Фурье для непериодических функций
Y = f(x) a <= x <=b
 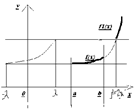
 f1(x) = f(x)
для функции f(x) выберем период 2μ >= b-a
Таким образом f(x) разложим на отрезке [a, b]
Пусть функция Y = f(x) [0, π] f1(x) = f(x)
для функции f(x) выберем период 2μ >= b-a
Таким образом f(x) разложим на отрезке [a, b]
Пусть функция Y = f(x) [0, π]
 а) f(x) = f(-x) – четная
Т = 2π
аo, аn, bn = 0
б)
а) f(x) = f(-x) – четная
Т = 2π
аo, аn, bn = 0
б)
  a0 = an = 0
a0 = an = 0
 Ряд будет содержать синусы
74. Комплексная форма ряда Фурье
Как известно из курса алгебры, экспонента от чисто мнимого аргумента определяется равенством
Ряд будет содержать синусы
74. Комплексная форма ряда Фурье
Как известно из курса алгебры, экспонента от чисто мнимого аргумента определяется равенством  Отсюда немедленно вытекают формулы Эйлера Отсюда немедленно вытекают формулы Эйлера
 справедливые для всех вещественных чисел
справедливые для всех вещественных чисел  Предполагая, что функция f разлагается в ряд Фурье, заменим в нем синусы и косинусы по формулам Эйлера:
Предполагая, что функция f разлагается в ряд Фурье, заменим в нем синусы и косинусы по формулам Эйлера:

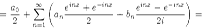
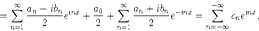 где использованы обозначения
где использованы обозначения
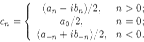 Вновь используя формулы Эйлера, преобразуем выражения для коэффициентов cn:
Вновь используя формулы Эйлера, преобразуем выражения для коэффициентов cn:
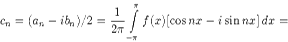 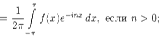  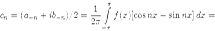  Итак, мы видим, что для всех значений n коэффициенты cn ищутся по одной формуле
Итак, мы видим, что для всех значений n коэффициенты cn ищутся по одной формуле
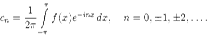 При этом имеет место разложение
При этом имеет место разложение
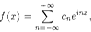 называемое комплексной формой ряда Фурье. Оно короче и симметричнее своего вещественного аналога и поэтому чаще используется в физике.
75. Операционное исчисление. Оригинал и изображение
01. Функция f(t) называется оригиналом если она удовлетворяет:
1) непрерывна или кусочно-непрерывна, однозначна, н-раз дифференцируемая для всех t >= 0
2) функция растет не быстрее чем некоторая показательная(???) функция, т.е. существуют такие «+» - числа М>0 и fо > 0 что выполняется:
|f(t)| <= M*e^(So*t) (1)
3) f(t) = 0, t<0
f(t) є D – принадлежность к классу оригиналов
02. Функция F(p) называется изображением если она вычисляется с помощью интеграла Лапласа:
называемое комплексной формой ряда Фурье. Оно короче и симметричнее своего вещественного аналога и поэтому чаще используется в физике.
75. Операционное исчисление. Оригинал и изображение
01. Функция f(t) называется оригиналом если она удовлетворяет:
1) непрерывна или кусочно-непрерывна, однозначна, н-раз дифференцируемая для всех t >= 0
2) функция растет не быстрее чем некоторая показательная(???) функция, т.е. существуют такие «+» - числа М>0 и fо > 0 что выполняется:
|f(t)| <= M*e^(So*t) (1)
3) f(t) = 0, t<0
f(t) є D – принадлежность к классу оригиналов
02. Функция F(p) называется изображением если она вычисляется с помощью интеграла Лапласа:
 Соответствие между оригиналом и изображением записывается
f(t) = F(p) (= с точками)
Основные свойства:
1. Линейность
Оригинал линейной комбинации функций равно линейной комбинации изображений с теми же коэффициентами.
Соответствие между оригиналом и изображением записывается
f(t) = F(p) (= с точками)
Основные свойства:
1. Линейность
Оригинал линейной комбинации функций равно линейной комбинации изображений с теми же коэффициентами.
 где a и b – произвольные комплексные числа.
2. Свойтсво аналитичности
Функция F(p), выражаемая интегралом Лапласа – есть функция аналитическая. Т.е. её можно раскладывать в степенной ряд, который можно почленно дифференцировать и интегрировать н-раз почленно.
3. Теорема единственности
Если 2 изображения равны между собой, то равны и оригиналы
76. Изображение простейших функций
Единичной функцией или функцией Хевисайда называется функция
где a и b – произвольные комплексные числа.
2. Свойтсво аналитичности
Функция F(p), выражаемая интегралом Лапласа – есть функция аналитическая. Т.е. её можно раскладывать в степенной ряд, который можно почленно дифференцировать и интегрировать н-раз почленно.
3. Теорема единственности
Если 2 изображения равны между собой, то равны и оригиналы
76. Изображение простейших функций
Единичной функцией или функцией Хевисайда называется функция
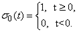 Очевидно, что показатель роста этой функции
Очевидно, что показатель роста этой функции 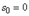 . Найдем L-изображение этой функции в области . Найдем L-изображение этой функции в области  : :
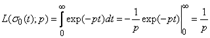 (exp = e, (-pt) – в степени)
Таким образом, (exp = e, (-pt) – в степени)
Таким образом,
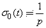 Тригонометрические функции:
Тригонометрические функции:
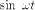 = =   = =  Гиперболические функции:
Гиперболические функции:
 = = 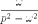
 = =  77. Изображение производных
77. Изображение производных

 78. Изображение интегралов
78. Изображение интегралов

|
 и распишем его подробнее:
и распишем его подробнее: 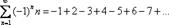 . У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности. Знакочередование обеспечивает множитель
. У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности. Знакочередование обеспечивает множитель  : если
: если  чётное, то будет знак «плюс», если нечётное – знак «минус». Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн». В практических примерах знакочередование членов ряда может обеспечивать не только множитель
чётное, то будет знак «плюс», если нечётное – знак «минус». Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн». В практических примерах знакочередование членов ряда может обеспечивать не только множитель 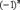 , но и подобные ему:
, но и подобные ему:  ,
, 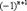 ,
,  , …. Например:
, …. Например: 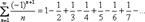 . Подводным камнем являются «обманки»:
. Подводным камнем являются «обманки»: 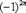 ,
, 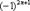 ,
,  и т.п. – такие множители не обеспечивают смену знака. Чтобы исследовать знакочередующийся ряд на сходимость необходимо использовать признак Лейбница.
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится. Или в два пункта: 1) Ряд является знакочередующимся. 2) Члены ряда убывают по модулю:
и т.п. – такие множители не обеспечивают смену знака. Чтобы исследовать знакочередующийся ряд на сходимость необходимо использовать признак Лейбница.
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится. Или в два пункта: 1) Ряд является знакочередующимся. 2) Члены ряда убывают по модулю:  . Причём, убывают монотонно. Если выполнены оба условия, то ряд сходится.
61. Знакопеременные ряды. Мажорирующие ряды. Условная и абсолютная сходимости рядов.
Знакопеременный ряд. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.
Мажорирующий ряд. Числовой ряд
. Причём, убывают монотонно. Если выполнены оба условия, то ряд сходится.
61. Знакопеременные ряды. Мажорирующие ряды. Условная и абсолютная сходимости рядов.
Знакопеременный ряд. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.
Мажорирующий ряд. Числовой ряд 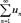 называется мажорирующим ряд
называется мажорирующим ряд  , если для любого n выполняется неравенство
, если для любого n выполняется неравенство  Абсолютная и условная сходимость.
Ряд
Абсолютная и условная сходимость.
Ряд 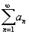 называется абсолютно сходящимся, если ряд
называется абсолютно сходящимся, если ряд 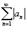 также сходится. Если ряд
также сходится. Если ряд 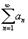 сходится абсолютно, то он является сходящимся (в обычном смысле).Обратное утверждение неверно. Ряд
сходится абсолютно, то он является сходящимся (в обычном смысле).Обратное утверждение неверно. Ряд  называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
62. Функциональные ряды. Основные определения.
Определение 1. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: U1(x) + U2(x) + … + Un(x) + … (1)
Определение 2. Если при X = X0 ряд (1) сходится, то X0 называется точкой сходимости ряда (1).
Определение 3. Множество всех значений х, при которых функциональный ряд сходится, называется областью сходимости этого ряда. Очевидно, что в области сходимости функционального ряда его сумма является функцией от х. Она обозначается S(x).
Степенной ряд – наиболее популярная разновидность функционального ряда, это ряд, в общий член Un(x) которого входят целые положительные степени независимой переменной x. Упрощенно степенной ряд записывается так:
называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
62. Функциональные ряды. Основные определения.
Определение 1. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: U1(x) + U2(x) + … + Un(x) + … (1)
Определение 2. Если при X = X0 ряд (1) сходится, то X0 называется точкой сходимости ряда (1).
Определение 3. Множество всех значений х, при которых функциональный ряд сходится, называется областью сходимости этого ряда. Очевидно, что в области сходимости функционального ряда его сумма является функцией от х. Она обозначается S(x).
Степенной ряд – наиболее популярная разновидность функционального ряда, это ряд, в общий член Un(x) которого входят целые положительные степени независимой переменной x. Упрощенно степенной ряд записывается так: 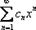 , где Cn – это многочлены, степени, факториалы, зависящие только от «эн». Простейший пример ряда:
, где Cn – это многочлены, степени, факториалы, зависящие только от «эн». Простейший пример ряда: 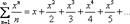 63. Теорема о непрерывности суммы функционального ряда.
Теорема. На любом отрезке целиком лежащем внутри интервала сходимости степенного ряда
63. Теорема о непрерывности суммы функционального ряда.
Теорема. На любом отрезке целиком лежащем внутри интервала сходимости степенного ряда  , сумма ряда есть непрерывная функция.
Доказательство. Каждая частичная сумма степенного ряда, очевидно, является непрерывной функцией. На любом отрезке целиком лежащем внутри интервала сходимости ряда сходимость является равномерной. Сумма ряда, являющаяся пределом равномерно сходящейся последовательности непрерывных функций, сама является непрерывной функцией. Теорема доказана.
64. Теоремы о почленном дифференцировании и интегрировании функциональных рядов.
Почленное интегрирование степенного ряда. Теорема. Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
Почленное дифференцирование степенного ряда. Теорема. Пусть степенной ряд
, сумма ряда есть непрерывная функция.
Доказательство. Каждая частичная сумма степенного ряда, очевидно, является непрерывной функцией. На любом отрезке целиком лежащем внутри интервала сходимости ряда сходимость является равномерной. Сумма ряда, являющаяся пределом равномерно сходящейся последовательности непрерывных функций, сама является непрерывной функцией. Теорема доказана.
64. Теоремы о почленном дифференцировании и интегрировании функциональных рядов.
Почленное интегрирование степенного ряда. Теорема. Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
Почленное дифференцирование степенного ряда. Теорема. Пусть степенной ряд
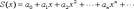 имеет радиус сходимости R. Тогда ряд
имеет радиус сходимости R. Тогда ряд
 полученный в результате почленного дифференцирования ряда
полученный в результате почленного дифференцирования ряда 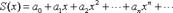 , также имеет радиус сходимости R. Производная суммы ряда
, также имеет радиус сходимости R. Производная суммы ряда 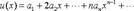 равна сумме ряда:
равна сумме ряда: 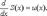 65. Степенные ряды Лемма.
Пусть r < R. Тогда
65. Степенные ряды Лемма.
Пусть r < R. Тогда 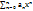 сходится на множестве |x| ≤ r абсолютно и равномерно.
Доказательство. Так как r < R, ряд
сходится на множестве |x| ≤ r абсолютно и равномерно.
Доказательство. Так как r < R, ряд 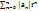 сходится. Так как |
сходится. Так как | 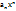 | ≤
| ≤ 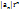 , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
66. 1-я и 2-я теоремы Абеля о сходимости степенного ряда.
, можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
66. 1-я и 2-я теоремы Абеля о сходимости степенного ряда.
 67. Аналитические функции и представление их степенным рядом.
Функция f называется аналитической в точке x0, если в некоторой окрестности этой точки она разлагается в степенной ряд:
67. Аналитические функции и представление их степенным рядом.
Функция f называется аналитической в точке x0, если в некоторой окрестности этой точки она разлагается в степенной ряд:  (1)
Естественной областью определения аналитической функции будет радиус сходимости ряда (1).
Пусть в окрестности точки (x0, y0, z0, q0) задана аналитическая функция f(x, y, z, q) своих 2n+2 переменных. Пусть далее w(y) – аналитическая функция в окрестности значения y0, и пусть z0 = w(y0), q0 = (grad w) y = y0
Тогда дифференциальное уравнение в достаточно малой окрестности точки (x0, y0) имеет ровно одно аналитическое решение z = ψ(x, y), которое при x = x0 принимает значение ψ(x0, y) = w(y). Коэффициенты степенного ряда для ψмогут быть получены применением к ψ обычного метода степенных рядов и приравниванием коэффициентов при соответствующих степенях с учетом начальных условий.
68. Ряды Фурье. Основные определения.
Говорят, что функция f(x) имеет период P, если f(x + P) = f(x) для всех значений x. Пусть период функции f(x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
1. Предположим, что функция f(x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:
(1)
Естественной областью определения аналитической функции будет радиус сходимости ряда (1).
Пусть в окрестности точки (x0, y0, z0, q0) задана аналитическая функция f(x, y, z, q) своих 2n+2 переменных. Пусть далее w(y) – аналитическая функция в окрестности значения y0, и пусть z0 = w(y0), q0 = (grad w) y = y0
Тогда дифференциальное уравнение в достаточно малой окрестности точки (x0, y0) имеет ровно одно аналитическое решение z = ψ(x, y), которое при x = x0 принимает значение ψ(x0, y) = w(y). Коэффициенты степенного ряда для ψмогут быть получены применением к ψ обычного метода степенных рядов и приравниванием коэффициентов при соответствующих степенях с учетом начальных условий.
68. Ряды Фурье. Основные определения.
Говорят, что функция f(x) имеет период P, если f(x + P) = f(x) для всех значений x. Пусть период функции f(x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
1. Предположим, что функция f(x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:
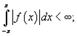 2. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции.
Определение 1. Последовательность функций фи1(х), фи2(х), фи3(х) называется нормированной на отрезке [a; b], если
2. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции.
Определение 1. Последовательность функций фи1(х), фи2(х), фи3(х) называется нормированной на отрезке [a; b], если
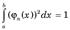 для всех n
Определение 2. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортогональной на отрезке [a; b], если
для всех n
Определение 2. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортогональной на отрезке [a; b], если
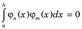 при
при  Определение 3. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортонормальной на отрезке [a; b], если она является нормированной и ортогональной, т.е.
Определение 3. Последовательность функций фи1(х), фи2(х), фи3(х) называется ортонормальной на отрезке [a; b], если она является нормированной и ортогональной, т.е.
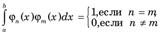 69. Коэффициенты ряда Фурье.
Коэффициенты Фурье функции f периода 2π:
69. Коэффициенты ряда Фурье.
Коэффициенты Фурье функции f периода 2π:

 или
или

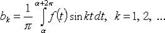 80. Интеграл Дюамеля
80. Интеграл Дюамеля
 81. Применение операционного исчисления
Задача Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами:
x ^(n) + a1 x^ (n - 1) + a2 x ^(n - 2) + … + a(n – 1) x ′ + an x = f (t),
x(0) = x0, x′ (0) = x1, x″ (0) = x2, …, x ^(n -1) (0) = x(n -1).
Начальные условия в этой задаче заданы в точке t0 = 0. Если начальные условия задаются в другой точке t0 ≠ 0, то заменой аргумента u = t - t0 их сдвигают в точку u0 = 0.
Метод решения этой задачи основан на теореме о дифференцировании оригинала. Предположим, что функция x(t), её производные до n-го порядка, правая часть f(t) являются функциями-оригиналами, и x(t) = X(p). Тогда
x ′(t) = p X(p) − x(0) = p X(p) − x0, x ″(t) = p2 X(p) − p x0− x1, …, x^(n)(t) = p^(n) X(p) − p ^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1), и изображение задачи будет иметь вид p^n X(p) − p^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1) +
+ a1(p^(n – 1) X(p) − p^(n – 2) x0 − p^(n – 3) x1 − … − x(n – 2)) + …
+a(n – 1) (p X(p) − x0) + a(n) X(p) = F(p), где F(p)= f (t) - изображение правой части уравнения. Это линейное относительно X(p) алгебраическое уравнение, решив которое, находим X(p). Оригинал этого изображения и будет решением задачи Коши.
Вычисление несобственных интегралов
Если f = F, g = G, то
81. Применение операционного исчисления
Задача Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами:
x ^(n) + a1 x^ (n - 1) + a2 x ^(n - 2) + … + a(n – 1) x ′ + an x = f (t),
x(0) = x0, x′ (0) = x1, x″ (0) = x2, …, x ^(n -1) (0) = x(n -1).
Начальные условия в этой задаче заданы в точке t0 = 0. Если начальные условия задаются в другой точке t0 ≠ 0, то заменой аргумента u = t - t0 их сдвигают в точку u0 = 0.
Метод решения этой задачи основан на теореме о дифференцировании оригинала. Предположим, что функция x(t), её производные до n-го порядка, правая часть f(t) являются функциями-оригиналами, и x(t) = X(p). Тогда
x ′(t) = p X(p) − x(0) = p X(p) − x0, x ″(t) = p2 X(p) − p x0− x1, …, x^(n)(t) = p^(n) X(p) − p ^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1), и изображение задачи будет иметь вид p^n X(p) − p^(n – 1) x0 − p^(n – 2) x1 − … − p x(n – 2) − x(n – 1) +
+ a1(p^(n – 1) X(p) − p^(n – 2) x0 − p^(n – 3) x1 − … − x(n – 2)) + …
+a(n – 1) (p X(p) − x0) + a(n) X(p) = F(p), где F(p)= f (t) - изображение правой части уравнения. Это линейное относительно X(p) алгебраическое уравнение, решив которое, находим X(p). Оригинал этого изображения и будет решением задачи Коши.
Вычисление несобственных интегралов
Если f = F, g = G, то
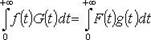 79. Свертка функций
79. Свертка функций
 Вариант из Интернета (возможно он будет получше):
Сверткой функций f1(t) и f2(t) называется функция
Вариант из Интернета (возможно он будет получше):
Сверткой функций f1(t) и f2(t) называется функция  Свёртка обозначается символом f1 * f2:
Свёртка обозначается символом f1 * f2:
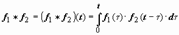 Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f1(t) и f2(t) не больше, чем на 1. Действительно, пусть
Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f1(t) и f2(t) не больше, чем на 1. Действительно, пусть 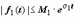 ,
, 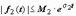 ,
,
 , тогда
, тогда 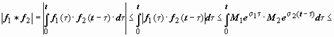
 , так как t < e^t.
, так как t < e^t.
 =
= 
 =
= 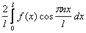
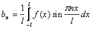 = 0
= 0  , где n =1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2 L выглядит так:
, где n =1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2 L выглядит так:
 71. Ряд Фурье для нечетных функций
Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
71. Ряд Фурье для нечетных функций
Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
 где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
 Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
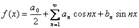 , где
, где 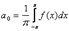
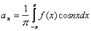
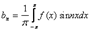 Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
72. Ряд Фурье для функций с периодом 2l
Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
72. Ряд Фурье для функций с периодом 2l
Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
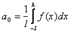 =
= 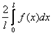
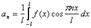 =
= 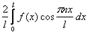 ;
;  = 0, где n=1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:
= 0, где n=1,2,...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:
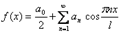 Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
Пусть f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
 где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
где n=1,2,...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
 Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке то
 , где
, где 

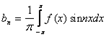 Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
73. Ряд Фурье для непериодических функций
Y = f(x) a <= x <=b
Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо: доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
73. Ряд Фурье для непериодических функций
Y = f(x) a <= x <=b


 f1(x) = f(x)
для функции f(x) выберем период 2μ >= b-a
Таким образом f(x) разложим на отрезке [a, b]
Пусть функция Y = f(x) [0, π]
f1(x) = f(x)
для функции f(x) выберем период 2μ >= b-a
Таким образом f(x) разложим на отрезке [a, b]
Пусть функция Y = f(x) [0, π]
 а) f(x) = f(-x) – четная
Т = 2π
аo, аn, bn = 0
б)
а) f(x) = f(-x) – четная
Т = 2π
аo, аn, bn = 0
б)

 a0 = an = 0
a0 = an = 0
 Ряд будет содержать синусы
74. Комплексная форма ряда Фурье
Как известно из курса алгебры, экспонента от чисто мнимого аргумента определяется равенством
Ряд будет содержать синусы
74. Комплексная форма ряда Фурье
Как известно из курса алгебры, экспонента от чисто мнимого аргумента определяется равенством  Отсюда немедленно вытекают формулы Эйлера
Отсюда немедленно вытекают формулы Эйлера
 справедливые для всех вещественных чисел
справедливые для всех вещественных чисел  Предполагая, что функция f разлагается в ряд Фурье, заменим в нем синусы и косинусы по формулам Эйлера:
Предполагая, что функция f разлагается в ряд Фурье, заменим в нем синусы и косинусы по формулам Эйлера:

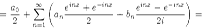
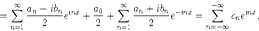 где использованы обозначения
где использованы обозначения
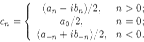 Вновь используя формулы Эйлера, преобразуем выражения для коэффициентов cn:
Вновь используя формулы Эйлера, преобразуем выражения для коэффициентов cn:
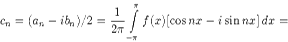
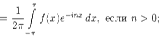

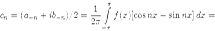
 Итак, мы видим, что для всех значений n коэффициенты cn ищутся по одной формуле
Итак, мы видим, что для всех значений n коэффициенты cn ищутся по одной формуле
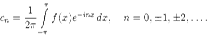 При этом имеет место разложение
При этом имеет место разложение
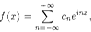 называемое комплексной формой ряда Фурье. Оно короче и симметричнее своего вещественного аналога и поэтому чаще используется в физике.
75. Операционное исчисление. Оригинал и изображение
01. Функция f(t) называется оригиналом если она удовлетворяет:
1) непрерывна или кусочно-непрерывна, однозначна, н-раз дифференцируемая для всех t >= 0
2) функция растет не быстрее чем некоторая показательная(???) функция, т.е. существуют такие «+» - числа М>0 и fо > 0 что выполняется:
|f(t)| <= M*e^(So*t) (1)
3) f(t) = 0, t<0
f(t) є D – принадлежность к классу оригиналов
02. Функция F(p) называется изображением если она вычисляется с помощью интеграла Лапласа:
называемое комплексной формой ряда Фурье. Оно короче и симметричнее своего вещественного аналога и поэтому чаще используется в физике.
75. Операционное исчисление. Оригинал и изображение
01. Функция f(t) называется оригиналом если она удовлетворяет:
1) непрерывна или кусочно-непрерывна, однозначна, н-раз дифференцируемая для всех t >= 0
2) функция растет не быстрее чем некоторая показательная(???) функция, т.е. существуют такие «+» - числа М>0 и fо > 0 что выполняется:
|f(t)| <= M*e^(So*t) (1)
3) f(t) = 0, t<0
f(t) є D – принадлежность к классу оригиналов
02. Функция F(p) называется изображением если она вычисляется с помощью интеграла Лапласа:
 Соответствие между оригиналом и изображением записывается
f(t) = F(p) (= с точками)
Основные свойства:
1. Линейность
Оригинал линейной комбинации функций равно линейной комбинации изображений с теми же коэффициентами.
Соответствие между оригиналом и изображением записывается
f(t) = F(p) (= с точками)
Основные свойства:
1. Линейность
Оригинал линейной комбинации функций равно линейной комбинации изображений с теми же коэффициентами.
 где a и b – произвольные комплексные числа.
2. Свойтсво аналитичности
Функция F(p), выражаемая интегралом Лапласа – есть функция аналитическая. Т.е. её можно раскладывать в степенной ряд, который можно почленно дифференцировать и интегрировать н-раз почленно.
3. Теорема единственности
Если 2 изображения равны между собой, то равны и оригиналы
76. Изображение простейших функций
Единичной функцией или функцией Хевисайда называется функция
где a и b – произвольные комплексные числа.
2. Свойтсво аналитичности
Функция F(p), выражаемая интегралом Лапласа – есть функция аналитическая. Т.е. её можно раскладывать в степенной ряд, который можно почленно дифференцировать и интегрировать н-раз почленно.
3. Теорема единственности
Если 2 изображения равны между собой, то равны и оригиналы
76. Изображение простейших функций
Единичной функцией или функцией Хевисайда называется функция
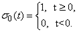 Очевидно, что показатель роста этой функции
Очевидно, что показатель роста этой функции 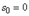 . Найдем L-изображение этой функции в области
. Найдем L-изображение этой функции в области  :
:
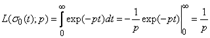 (exp = e, (-pt) – в степени)
Таким образом,
(exp = e, (-pt) – в степени)
Таким образом,
 Тригонометрические функции:
Тригонометрические функции:
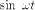 =
= 
 =
=  Гиперболические функции:
Гиперболические функции:
 =
= 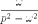
 =
=  77. Изображение производных
77. Изображение производных

 78. Изображение интегралов
78. Изображение интегралов




 un= 0.
un= 0.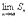 = S. Тогда имеет место также равенство
= S. Тогда имеет место также равенство 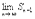 = S, так как при n
= S, так как при n 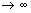 и (n-1)
и (n-1) 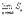 -
-  =
=  =
= 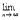 un =0, что и требовалось доказать.
un =0, что и требовалось доказать. un ≠0, то ряд u1+u2+…+un… расходится.
un ≠0, то ряд u1+u2+…+un… расходится. расходится, так как
расходится, так как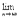 un =
un = 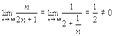 .
. un =0 не следует, что ряд сходится.
un =0 не следует, что ряд сходится.