51. Системы дифференциальных уравнений. Основные определения.
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).
Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например,  не является дифференциальным уравнением.
Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y (x), имеющая на некотором интервале (a, b) производные не является дифференциальным уравнением.
Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y (x), имеющая на некотором интервале (a, b) производные  до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести кквадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.
Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Общий вид: до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести кквадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.
Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Общий вид:
 Подклассом линейных уравнений являются однородные дифференциальные уравнения — уравнения, которые не содержат свободного члена: r (x) = 0. Для однородных дифференциальных уравнений выполняетсяпринцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
52. Метод исключения решений системы дифференциальных уравнений.
Системы дифференциальных уравнений n –го порядка можно решать сведением к уравнению n –го порядка. Такой метод решения систем называется методом исключения.
Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка
Подклассом линейных уравнений являются однородные дифференциальные уравнения — уравнения, которые не содержат свободного члена: r (x) = 0. Для однородных дифференциальных уравнений выполняетсяпринцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
52. Метод исключения решений системы дифференциальных уравнений.
Системы дифференциальных уравнений n –го порядка можно решать сведением к уравнению n –го порядка. Такой метод решения систем называется методом исключения.
Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка
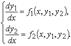 Исключим функцию y 2. Для этого сначала выразим y 2 через x и y 1 из первого уравнения системы, затем продифференцируем по x первое уравнение системы, заменяя y 2 полученным для него выражением, а производную y 2 − правой частью второго уравнения системы:
Исключим функцию y 2. Для этого сначала выразим y 2 через x и y 1 из первого уравнения системы, затем продифференцируем по x первое уравнение системы, заменяя y 2 полученным для него выражением, а производную y 2 − правой частью второго уравнения системы:
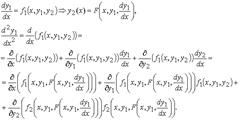 Получили обыкновенное дифференциальное уравнение 2 –го порядка
Получили обыкновенное дифференциальное уравнение 2 –го порядка
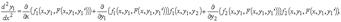 Таким же образом решают методом исключения произвольные системы n –го порядка: дифференцируют уравнения системы и, последовательно исключая функции y 2,..., yn и их производные, сводят систему к одному дифференциальному уравнению n –го порядка относительно y 1.
53. Метод Эйлера решения системы дифференциальных уравнений.
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений.
Ломаная Эйлера (красная линия) — приближённое решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)
Таким же образом решают методом исключения произвольные системы n –го порядка: дифференцируют уравнения системы и, последовательно исключая функции y 2,..., yn и их производные, сводят систему к одному дифференциальному уравнению n –го порядка относительно y 1.
53. Метод Эйлера решения системы дифференциальных уравнений.
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений.
Ломаная Эйлера (красная линия) — приближённое решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)
 Пусть дана задача Коши для уравнения первого порядка
Пусть дана задача Коши для уравнения первого порядка
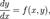
 где функция
где функция 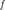 определена на некоторой области определена на некоторой области 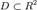 . Решение разыскивается на интервале . Решение разыскивается на интервале  . На этом интервале введем узлы . На этом интервале введем узлы
 Приближенное решение в узлах
Приближенное решение в узлах  , которое обозначим через , которое обозначим через  определяется по формуле определяется по формуле
 Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
54. Метод суперпозиций решений системы дифференциальных уравнений.
Принцип суперпозиции: Если y 1(x) и y 2(x) — решения неоднородных линейных уравнений L (y) = f 1(x) и L (y) = f 2(x), то их сумма y (x) = y 1(x) + y 2(x) является решением уравнения L (y) = f 1(x) + f 2(x).
57. Признак Даламбера сходимости ряда.
Если для числового ряда
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
54. Метод суперпозиций решений системы дифференциальных уравнений.
Принцип суперпозиции: Если y 1(x) и y 2(x) — решения неоднородных линейных уравнений L (y) = f 1(x) и L (y) = f 2(x), то их сумма y (x) = y 1(x) + y 2(x) является решением уравнения L (y) = f 1(x) + f 2(x).
57. Признак Даламбера сходимости ряда.
Если для числового ряда
 существует такое число
существует такое число  , ,  , что начиная с некоторого номера выполняется неравенство , что начиная с некоторого номера выполняется неравенство
 то данный ряд абсолютно сходится; если же, начиная с некоторого номера
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
 то ряд расходится.
Доказательство:
1.
то ряд расходится.
Доказательство:
1.  , тогда существует , тогда существует  , существует , существует  , для любого , для любого 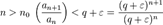 . Ряд из . Ряд из  сходится (как геометрическая прогрессия). Значит, ряд из сходится (как геометрическая прогрессия). Значит, ряд из  сходится (по признаку сравнения).
2. сходится (по признаку сравнения).
2.  , тогда существует , тогда существует 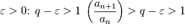 . .  для любого для любого  . Тогда . Тогда  не стремится к нулю и ряд расходится.
58. Радикальный признак Коши сходимости ряда.
Если для числового ряда не стремится к нулю и ряд расходится.
58. Радикальный признак Коши сходимости ряда.
Если для числового ряда
 с неотрицательными членами существует такое число
с неотрицательными членами существует такое число  , ,  , что, начиная с некоторого номера, выполняется неравенство , что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.
Условие радикального признака равносильно следующему: , то данный ряд сходится.
Условие радикального признака равносильно следующему:
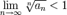 То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Если для ряда
 , то
если , то
если  ряд сходится,
если ряд сходится,
если  ряд расходится,
если ряд расходится,
если  вопрос о сходимости ряда остается открытым. вопрос о сходимости ряда остается открытым.
|
|
 не является дифференциальным уравнением.
Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y (x), имеющая на некотором интервале (a, b) производные
не является дифференциальным уравнением.
Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y (x), имеющая на некотором интервале (a, b) производные  до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести кквадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.
Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Общий вид:
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести кквадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.
Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Общий вид:
 Подклассом линейных уравнений являются однородные дифференциальные уравнения — уравнения, которые не содержат свободного члена: r (x) = 0. Для однородных дифференциальных уравнений выполняетсяпринцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
52. Метод исключения решений системы дифференциальных уравнений.
Системы дифференциальных уравнений n –го порядка можно решать сведением к уравнению n –го порядка. Такой метод решения систем называется методом исключения.
Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка
Подклассом линейных уравнений являются однородные дифференциальные уравнения — уравнения, которые не содержат свободного члена: r (x) = 0. Для однородных дифференциальных уравнений выполняетсяпринцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
52. Метод исключения решений системы дифференциальных уравнений.
Системы дифференциальных уравнений n –го порядка можно решать сведением к уравнению n –го порядка. Такой метод решения систем называется методом исключения.
Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка
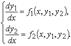 Исключим функцию y 2. Для этого сначала выразим y 2 через x и y 1 из первого уравнения системы, затем продифференцируем по x первое уравнение системы, заменяя y 2 полученным для него выражением, а производную y 2 − правой частью второго уравнения системы:
Исключим функцию y 2. Для этого сначала выразим y 2 через x и y 1 из первого уравнения системы, затем продифференцируем по x первое уравнение системы, заменяя y 2 полученным для него выражением, а производную y 2 − правой частью второго уравнения системы:
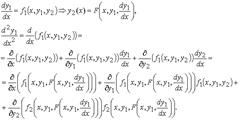 Получили обыкновенное дифференциальное уравнение 2 –го порядка
Получили обыкновенное дифференциальное уравнение 2 –го порядка
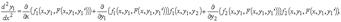 Таким же образом решают методом исключения произвольные системы n –го порядка: дифференцируют уравнения системы и, последовательно исключая функции y 2,..., yn и их производные, сводят систему к одному дифференциальному уравнению n –го порядка относительно y 1.
53. Метод Эйлера решения системы дифференциальных уравнений.
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений.
Ломаная Эйлера (красная линия) — приближённое решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)
Таким же образом решают методом исключения произвольные системы n –го порядка: дифференцируют уравнения системы и, последовательно исключая функции y 2,..., yn и их производные, сводят систему к одному дифференциальному уравнению n –го порядка относительно y 1.
53. Метод Эйлера решения системы дифференциальных уравнений.
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений.
Ломаная Эйлера (красная линия) — приближённое решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)
 Пусть дана задача Коши для уравнения первого порядка
Пусть дана задача Коши для уравнения первого порядка
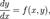
 где функция
где функция 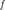 определена на некоторой области
определена на некоторой области 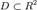 . Решение разыскивается на интервале
. Решение разыскивается на интервале  . На этом интервале введем узлы
. На этом интервале введем узлы
 Приближенное решение в узлах
Приближенное решение в узлах  , которое обозначим через
, которое обозначим через  определяется по формуле
определяется по формуле
 Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
54. Метод суперпозиций решений системы дифференциальных уравнений.
Принцип суперпозиции: Если y 1(x) и y 2(x) — решения неоднородных линейных уравнений L (y) = f 1(x) и L (y) = f 2(x), то их сумма y (x) = y 1(x) + y 2(x) является решением уравнения L (y) = f 1(x) + f 2(x).
57. Признак Даламбера сходимости ряда.
Если для числового ряда
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
54. Метод суперпозиций решений системы дифференциальных уравнений.
Принцип суперпозиции: Если y 1(x) и y 2(x) — решения неоднородных линейных уравнений L (y) = f 1(x) и L (y) = f 2(x), то их сумма y (x) = y 1(x) + y 2(x) является решением уравнения L (y) = f 1(x) + f 2(x).
57. Признак Даламбера сходимости ряда.
Если для числового ряда
 существует такое число
существует такое число  ,
,  , что начиная с некоторого номера выполняется неравенство
, что начиная с некоторого номера выполняется неравенство
 то данный ряд абсолютно сходится; если же, начиная с некоторого номера
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
 то ряд расходится.
Доказательство:
1.
то ряд расходится.
Доказательство:
1.  , тогда существует
, тогда существует  , существует
, существует  , для любого
, для любого 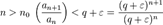 . Ряд из
. Ряд из  сходится (как геометрическая прогрессия). Значит, ряд из
сходится (как геометрическая прогрессия). Значит, ряд из  сходится (по признаку сравнения).
2.
сходится (по признаку сравнения).
2.  , тогда существует
, тогда существует 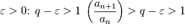 .
.  для любого
для любого  . Тогда
. Тогда  не стремится к нулю и ряд расходится.
58. Радикальный признак Коши сходимости ряда.
Если для числового ряда
не стремится к нулю и ряд расходится.
58. Радикальный признак Коши сходимости ряда.
Если для числового ряда
 с неотрицательными членами существует такое число
с неотрицательными членами существует такое число  ,
,  , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.
Условие радикального признака равносильно следующему:
, то данный ряд сходится.
Условие радикального признака равносильно следующему:
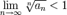 То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:





 , то
если
, то
если  ряд сходится,
если
ряд сходится,
если  ряд расходится,
если
ряд расходится,
если  вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.



