
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства двократного інтегралаСодержание книги Поиск на нашем сайте
1 – Двукратный интергал по всей области D равен сумме двукратный интегралов по областям D1,D2, которые получаются,если ращбить область D прямой параллельной одной из координатних осей т.е. 2 – Если для функции f(x,y) в области D площадью S m,M – соответственно наименьшее и наибольшее значение этой функции,то двукратный интерграл лежит в пределах 3 – Если функція f(x;y) является непрерывной функцией в области D прощадью S, то Вычисление площадей и объемов с помощью двойного интеграла. Вычисление площади плоской фигуры Площадь плоской фигуры, ограниченной областью D, находится по формуле Вычисление площади пространственных поверхностей Если гладкая однозначная поверхность задана уравнением z = f (x, y), то площадь этой поверхности выражается формулой Вычисление объема тела Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f (x, y), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости хОу область D, вычисляется по формуле т.е. равен модулю двойного интеграла. Вычисление объемов тел более сложной формы сводится к вычислению алгебраической суммы объемов нескольких цилиндрических тел.
| 16. Двойной интеграл в полярных координатах.
Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат:  Двойной интеграл в полярных координатах описывается формулой
Двойной интеграл в полярных координатах описывается формулой
 17. Площадь поверхности.
Площадь поверхности S выражается с помощью поверхностного интеграла в виде
17. Площадь поверхности.
Площадь поверхности S выражается с помощью поверхностного интеграла в виде
 Если поверхность S состоит из нескольких частей Si, то для вычисления поверхностного интеграла можно использовать свойство аддитивности:
Если поверхность S состоит из нескольких частей Si, то для вычисления поверхностного интеграла можно использовать свойство аддитивности:
 18. Тройной интеграл. Определение, геометрический, физический смысл.
Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.
Объем тела U в декартовых координатах Oxyz выражается формулой
18. Тройной интеграл. Определение, геометрический, физический смысл.
Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.
Объем тела U в декартовых координатах Oxyz выражается формулой
 В цилиндрических координатах объем тела равен
В цилиндрических координатах объем тела равен
 В сферических координатах, соответственно, используется формула
В сферических координатах, соответственно, используется формула
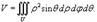 Физические приложения тройных интегралов
Пусть тело занимает объем U и его объемная плотность в точке M(x,y,z) задана функцией ρ(x,y,z). Тогда масса тела m вычисляется с помощью тройного интеграла:
Физические приложения тройных интегралов
Пусть тело занимает объем U и его объемная плотность в точке M(x,y,z) задана функцией ρ(x,y,z). Тогда масса тела m вычисляется с помощью тройного интеграла:
 19. Вычисление тройного интеграла.
Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.
Формула сведения тройного интеграла к повторному:
20. Замена переменных в двойных и тройных интегралах.
Для вычисления двойного интеграла
19. Вычисление тройного интеграла.
Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.
Формула сведения тройного интеграла к повторному:
20. Замена переменных в двойных и тройных интегралах.
Для вычисления двойного интеграла  иногда удобнее перейти в другую систему координат.
Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции.
В новой системе координат вычисление двойного интеграла значительно упрощается.
Замена переменных в двойном интеграле описывается формулой иногда удобнее перейти в другую систему координат.
Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции.
В новой системе координат вычисление двойного интеграла значительно упрощается.
Замена переменных в двойном интеграле описывается формулой
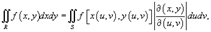 где выражение
где выражение  представляет собой так называемый якобиан преобразования представляет собой так называемый якобиан преобразования
 , а S − образ области интегрирования R, который можно найти с помощью подстановки , а S − образ области интегрирования R, который можно найти с помощью подстановки
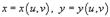 в определение области R.
Тройной:
Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:
в определение области R.
Тройной:
Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:
 Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
 Предполагается, что выполнены следующие условия:
1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w) отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Предполагается, что выполнены следующие условия:
1. Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2. Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3. Якобиан преобразования I (u,v,w) отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
 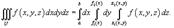 ф. замены переменных в тройном интеграле: ф. замены переменных в тройном интеграле: 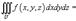

| ||
21. Цилиндрические координаты:
Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (z), которая задаёт высоту точки над плоскостью.
x=ρcosφ, y=ρsinφ, z=h,
(ρ≥0,0≤φ≤2π,−∞<h<+∞)
 Сферические координаты.
Положение точки М в сферической системе координат задается тройкой чисел r, φ и θ, где r – расстояние от начала координат до точки M (0<= r<∞); φ – угол, образованный проекцией радиус-вектора OM на плоскость Оху с положительным направлением оси Ох (0<=ф<2 п); θ – угол между положительным направлением оси Ozи радиус-вектором точки М (0<=θ<= п).
Сферические координаты.
Положение точки М в сферической системе координат задается тройкой чисел r, φ и θ, где r – расстояние от начала координат до точки M (0<= r<∞); φ – угол, образованный проекцией радиус-вектора OM на плоскость Оху с положительным направлением оси Ох (0<=ф<2 п); θ – угол между положительным направлением оси Ozи радиус-вектором точки М (0<=θ<= п).
 x=rcosφcosθ,
y=rsinφcosθ,
z=rsinθ,
(r≥0, 0≤φ≤2π,−π/2≤θ≤π/2)
22. Криволинейные интегралы 1-го и 2-го рода
Интеграл 1-го рода берется по длине дуги, 2-го – по координатам. x=rcosφcosθ,
y=rsinφcosθ,
z=rsinθ,
(r≥0, 0≤φ≤2π,−π/2≤θ≤π/2)
22. Криволинейные интегралы 1-го и 2-го рода
Интеграл 1-го рода берется по длине дуги, 2-го – по координатам.
 Пусть имеется дуга. Задана ф-ция f(x,y), дугу разобьем на n –частей и точки деления соединим ортами. Составляем интэгральную сумму
І=
Пусть имеется дуга. Задана ф-ция f(x,y), дугу разобьем на n –частей и точки деления соединим ортами. Составляем интэгральную сумму
І=  lim
lim  1) dl=
1) dl=  dx
2) dl= dx
2) dl= 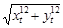 dt
3) dl= dt
3) dl=  dU
Этот интэграл не зависит от способов разбиения дуги на части, а зависит от интэгральной ф-ции.
Св-ва
1) dU
Этот интэграл не зависит от способов разбиения дуги на части, а зависит от интэгральной ф-ции.
Св-ва
1)  -кривол. инт. 2-го рода
2) -кривол. инт. 2-го рода
2)  Вычисление интэграла 2-го рода
Вычисление интэграла 2-го рода
 L: L: 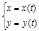  Теор. Пусть дан криволинейный интэграл P(x,y) и Q(x,y) непрерывн. в кажд. т. дуги L, а также непрерывн. ф-ции x(t) b y(t) вместе со своими производными
Теор. Пусть дан криволинейный интэграл P(x,y) и Q(x,y) непрерывн. в кажд. т. дуги L, а также непрерывн. ф-ции x(t) b y(t) вместе со своими производными  , тогда сущ. предел:
A= , тогда сущ. предел:
A=  B=
B=  Разбиваем дугу MN на n-частей
Разбиваем дугу MN на n-частей
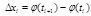 

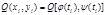 К преращениям прим. т. Лагранжа
К преращениям прим. т. Лагранжа

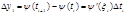 Пределы интегральных сумм А и В имеет вид:
A=
Пределы интегральных сумм А и В имеет вид:
A= 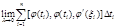 B=
B= 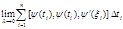
 24 Применение криволинейных интегралов первого рода
Применение в геометрии
Пусть в плоскости Oxy задана кривая AB, и на этой кривой определена функция
24 Применение криволинейных интегралов первого рода
Применение в геометрии
Пусть в плоскости Oxy задана кривая AB, и на этой кривой определена функция  . 1. Площадь цилиндрической поверхности, определенной функцией . 1. Площадь цилиндрической поверхности, определенной функцией  , определяют по формуле , определяют по формуле 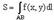 . 2. Длину кривой AB определяют по формуле . 2. Длину кривой AB определяют по формуле 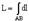 .
Применение в механике
Пусть дана материальная кривая L, плотность на которой меняется по формуле .
Применение в механике
Пусть дана материальная кривая L, плотность на которой меняется по формуле  . 1. Масса кривой: . 1. Масса кривой:  . 2. Статические моменты кривой относительно осей Ox и Oy: . 2. Статические моменты кривой относительно осей Ox и Oy: 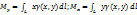 3. Координаты центра тяжести
3. Координаты центра тяжести  : :  , ,  4. Моменты инерции кривой относительно осей Ox, Oy и начала координат:
4. Моменты инерции кривой относительно осей Ox, Oy и начала координат: 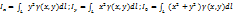 25 Формула Грина
Пусть в плоскости O xy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция
25 Формула Грина
Пусть в плоскости O xy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция  с непрерывными частными производными первого порядка
с непрерывными частными производными первого порядка  . Тогда справедлива формула Грина . Тогда справедлива формула Грина
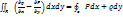 где символ
где символ  указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если  , то формула Грина принимает вид , то формула Грина принимает вид  где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией  Ротором или вихрем векторного поля
Ротором или вихрем векторного поля  называется вектор, обозначаемый называется вектор, обозначаемый  или или  и равный и равный
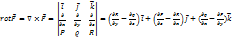 Формула Грина в векторной форме записывается в виде
Формула Грина в векторной форме записывается в виде  Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух
координат.
Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух
координат.
| 26) Условие независимости криволинейных интегралов от пути интегрирования.
Теорема:
Пусть дан  , где P(x,y) и Q(x,y) - непрерывны в области D, ограниченной границей L, и существуют , где P(x,y) и Q(x,y) - непрерывны в области D, ограниченной границей L, и существуют  , ,  .
Для того чтобы .
Для того чтобы 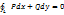 необходимо и достаточно, чтобы необходимо и достаточно, чтобы 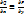 (1).
Доказательство:
1) Необходимость:
Запишем формулу Грина: (1).
Доказательство:
1) Необходимость:
Запишем формулу Грина:
 Предположим
Предположим   в т. М0(х0,у0) в т. М0(х0,у0)
 |M0 >0 M0 |M0 >0 M0  Окружим эту точку контуром L* и получим область D*
Окружим эту точку контуром L* и получим область D*

 , но по условию , но по условию  . И это противоречие доказывает теорему.
27) Поверхностный интеграл. Основные определения. Физический смысл.
В R3 расположена область V, ограниченная поверхностью σ. Эта поверхность разбита на n частей и их сумма Δσi. Пусть в каждой точке поверхности задан вектор F=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k. В каждом элементе Δσi возьмём точки Mi и проведём единичную нормаль ni0 (Mi):
Запишем скалярное произведение: (Fi, ni0)=|F|*|ni0|*cos(Fi, ni0)
ni0=cos(ni0, OX)i+cos(ni0, OY)j+cos(ni0, OZ)k
Составим интегральную сумму и перейдём к пределу: . И это противоречие доказывает теорему.
27) Поверхностный интеграл. Основные определения. Физический смысл.
В R3 расположена область V, ограниченная поверхностью σ. Эта поверхность разбита на n частей и их сумма Δσi. Пусть в каждой точке поверхности задан вектор F=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k. В каждом элементе Δσi возьмём точки Mi и проведём единичную нормаль ni0 (Mi):
Запишем скалярное произведение: (Fi, ni0)=|F|*|ni0|*cos(Fi, ni0)
ni0=cos(ni0, OX)i+cos(ni0, OY)j+cos(ni0, OZ)k
Составим интегральную сумму и перейдём к пределу:
 Fi, ni0)Δσi= Fi, ni0)Δσi=  (1)
Если вектор F скорость течения жидкости протекающей через площадь Δσi за единицу времени, то интеграл (1) – это вся масса жидкости протекающей через всю поверхность σ за единицу времени.
28) Поверхностный интеграл II рода.
Запишем в проекциях:
cos(n0, OX)d (1)
Если вектор F скорость течения жидкости протекающей через площадь Δσi за единицу времени, то интеграл (1) – это вся масса жидкости протекающей через всю поверхность σ за единицу времени.
28) Поверхностный интеграл II рода.
Запишем в проекциях:
cos(n0, OX)d  =dydz
cos(n0, OY)d =dydz
cos(n0, OY)d  =dxdz
cos(n0, OZ)d =dxdz
cos(n0, OZ)d  =dxdy
Учитывая, что ni0=cos(ni0, OX)i+cos(ni0, OY)j+cos(ni0, OZ)k - можно записать: =dxdy
Учитывая, что ni0=cos(ni0, OX)i+cos(ni0, OY)j+cos(ni0, OZ)k - можно записать:
 Его знак зависит от обхода поверхности σ, cos>0 “+”
cos<0 “-“
29) Формула Стокса.
Пусть в пространстве R3, есть плоскость V и поверхность σ: z=f(x,y). Задан вектор F, с непрерывными координатами x,y,z.
F=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k
n= cos(n, OX)i+cos(n, OY)j+cos(n, OZ)k
cos(n,OX)=
Его знак зависит от обхода поверхности σ, cos>0 “+”
cos<0 “-“
29) Формула Стокса.
Пусть в пространстве R3, есть плоскость V и поверхность σ: z=f(x,y). Задан вектор F, с непрерывными координатами x,y,z.
F=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k
n= cos(n, OX)i+cos(n, OY)j+cos(n, OZ)k
cos(n,OX)= 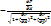 cos(n,OY)=
cos(n,OY)= 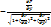 cos(n,OZ)=
cos(n,OZ)=  Для вывода формулы воспользуемся следующей символической записью:
Для вывода формулы воспользуемся следующей символической записью:
 =
= cos(n, OX)( =
= cos(n, OX)( )-cos(n, OY)( )-cos(n, OY)( )+cos(n, OZ)( )+cos(n, OZ)( )=
= )=
= 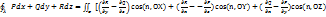 ]dσ= ]dσ=  30) Формула Остроградского.
Пусть в пространстве R3, есть плоскость V и поверхность σ: z=f(x,y).
σ = σ1+σ2+σ3
σ1:z=f1(x,y); cos(n,OZ)<0 “-“
σ2:z=f2(x,y); cos(n,OZ)>0 “+“
σ3:z=f3(x,y); cos(n,OZ)=0
30) Формула Остроградского.
Пусть в пространстве R3, есть плоскость V и поверхность σ: z=f(x,y).
σ = σ1+σ2+σ3
σ1:z=f1(x,y); cos(n,OZ)<0 “-“
σ2:z=f2(x,y); cos(n,OZ)>0 “+“
σ3:z=f3(x,y); cos(n,OZ)=0

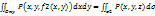


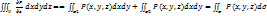 Аналогично понимаем:
Аналогично понимаем:

 В результате получаем:
В результате получаем:

| |||
31. Основные определения теории поля.
Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке M этой области соответствует определенное число U=U(M), говорят, что в области определено скалярное поле. Если в каждой точке M области пространства соответствует вектор  , то говорят, что задано векторное поое.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке.
Функции скалярного поля: , то говорят, что задано векторное поое.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке.
Функции скалярного поля:
 .
32. Производная по направлению. Градиент.
Возьмем в пространстве, где задано поле U=U(x, y, z), некоторую точку M и найдем скорость изменения функции U при движении точки M в произвольном направлении λ. Пусть вектор λ имеет начало в точке M и направляющие его косинусы. .
32. Производная по направлению. Градиент.
Возьмем в пространстве, где задано поле U=U(x, y, z), некоторую точку M и найдем скорость изменения функции U при движении точки M в произвольном направлении λ. Пусть вектор λ имеет начало в точке M и направляющие его косинусы.
 Приращение функции U, возникающее при переходе от точки M к некоторой точке M1 в направлении вектора λ определяется как
Приращение функции U, возникающее при переходе от точки M к некоторой точке M1 в направлении вектора λ определяется как  Или
Или  .
Тогда .
Тогда  Производной от функции U=U(M) в точке M по направлению λ называется предел
Производной от функции U=U(M) в точке M по направлению λ называется предел
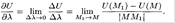 Градиент.
Вектор, координатами которого являются значения частных производных функции U(x,y,z) в точке M(x,y,z), называют градиентом функции и обозначают gradU.
Градиент.
Вектор, координатами которого являются значения частных производных функции U(x,y,z) в точке M(x,y,z), называют градиентом функции и обозначают gradU.
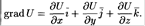 gradU — векторная величина.
gradU — векторная величина.
  Градиент функции указывает направление наибыстрейшего возрастания функции.
Наибольшая скорость изменения функции U в точке M равна:
Градиент функции указывает направление наибыстрейшего возрастания функции.
Наибольшая скорость изменения функции U в точке M равна:
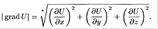 33. Ротор, дивергенция векторного поля
Дивергенция векторного поля
Дивергенция характеризует распределение и интенсивность источников и стоков поля.
Дивергенцией (расходимостью) векторного поля
33. Ротор, дивергенция векторного поля
Дивергенция векторного поля
Дивергенция характеризует распределение и интенсивность источников и стоков поля.
Дивергенцией (расходимостью) векторного поля
 в точке M называется скаляр вида
в точке M называется скаляр вида  и обозначается и обозначается
 .
Дивергенцией векторного поля в точке M называется предел отношения потока поля через замкнутую поверхность S, окружающую точку M, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку M (V -> 0)
Ротор.
Ротором вектора a в точке M называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора а по контуру L плоской площадки S, перпендикулярной этому направлению, к площади этой площадки. .
Дивергенцией векторного поля в точке M называется предел отношения потока поля через замкнутую поверхность S, окружающую точку M, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку M (V -> 0)
Ротор.
Ротором вектора a в точке M называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора а по контуру L плоской площадки S, перпендикулярной этому направлению, к площади этой площадки.


 34. Оператор Гамильтона.
Векторные операции первого порядка удобно записывать с помощью оператора Гамильтона
34. Оператор Гамильтона.
Векторные операции первого порядка удобно записывать с помощью оператора Гамильтона
 Применяя оператор Гамильтона, получим дифф. Операции первого порядка:
1.
Применяя оператор Гамильтона, получим дифф. Операции первого порядка:
1.  2.
2.  3.
3. 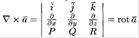 35. Потенциальное, гармоническое, соленоидальное поля.
Векторное поле называется соленоидальным, если во всех точках его дивергенция равно нулю.
Свойства:
1. В соленоидальном поле поток вектора через любую замкнутую поверхность равен нулю.
2. Соленоидальное поле является полем ротора некоторого векторного поля, т.е. если div a= 0, то существует такое поле b, что a=rot b. Вектор b называется векторным потенциалом поля а.
3. В соленоидальном поле поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение (интенсивность трубки).
Векторное поле называется потенциальным, если во всех точках поля ротор равен нулю.
Свойства:
1. Циркуляция потенциального поля по любому замкнутому полю в этом контуре равна нулю.
2. В потенциальном поле криволинейный интеграл
35. Потенциальное, гармоническое, соленоидальное поля.
Векторное поле называется соленоидальным, если во всех точках его дивергенция равно нулю.
Свойства:
1. В соленоидальном поле поток вектора через любую замкнутую поверхность равен нулю.
2. Соленоидальное поле является полем ротора некоторого векторного поля, т.е. если div a= 0, то существует такое поле b, что a=rot b. Вектор b называется векторным потенциалом поля а.
3. В соленоидальном поле поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение (интенсивность трубки).
Векторное поле называется потенциальным, если во всех точках поля ротор равен нулю.
Свойства:
1. Циркуляция потенциального поля по любому замкнутому полю в этом контуре равна нулю.
2. В потенциальном поле криволинейный интеграл  вдоль любой кривой L с началом в точке M1 и концом в точке M2 зависит только от положения точек и не зависит от формы кривой.
3. Потенциальное поле является полем градиента некоторой скалярной функции U(x,y,z), т.е. если rot a=0, то существует функция U(x,y,z) такая, что a=gradU.
Векторное поле называется гармоническим, если оно одновременно является потенциальным и соленоидальным (rot a=0 и div a=0). вдоль любой кривой L с началом в точке M1 и концом в точке M2 зависит только от положения точек и не зависит от формы кривой.
3. Потенциальное поле является полем градиента некоторой скалярной функции U(x,y,z), т.е. если rot a=0, то существует функция U(x,y,z) такая, что a=gradU.
Векторное поле называется гармоническим, если оно одновременно является потенциальным и соленоидальным (rot a=0 и div a=0).
| 36. Дифференциальные уравнения. Основные определения. Поле направлений.
Если искомая функция зависит от одной переменной, то диф. ур. называется обыкновенным диф. ур., если от нескольких – ур. в частных производных.
Порядком диф. ур. называется наивысший порядок производной, входящей в данное ур.
Диф. ур. 1-го порядка: F (x, y, y/) = 0
Общим решением называется функция y = φ (x, c), где с – константа.
Общим интегралом называется функция Φ (x, y, c) = 0.
Частным решением называется решение, записанное в виде y0 = φ (x0, c0).
Поле направлений — геометрическая интерпретация множества линейных элементов, соответствующих системе обыкновенных дифференциальных уравнений.
 Для системы в симметричной форме:
Для системы в симметричной форме:
 37. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение первого порядка y' = f (x,y) называется уравнением с разделяющимися переменными, если функцию f (x,y) можно представить в виде произведения двух функций, зависящих только от x и y:
37. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение первого порядка y' = f (x,y) называется уравнением с разделяющимися переменными, если функцию f (x,y) можно представить в виде произведения двух функций, зависящих только от x и y:
 Рассматривая производную y' как отношение дифференциалов, перенесем dx в правую часть и разделим уравнение на h(y):
Рассматривая производную y' как отношение дифференциалов, перенесем dx в правую часть и разделим уравнение на h(y):
 Если найдется число x0, при котором h(x0) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.
Обозначив
Если найдется число x0, при котором h(x0) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.
Обозначив  , запишем уравнение в форме: , запишем уравнение в форме:
 Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
 Вычисляя интегралы, получаем выражение
Вычисляя интегралы, получаем выражение 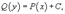 .
37. Составление дифференциальных уравнений по его решению.
Для того, чтобы по известному общему решению .
37. Составление дифференциальных уравнений по его решению.
Для того, чтобы по известному общему решению  восстановить дифференциальное уравнение, нужно исключить С из равенств: восстановить дифференциальное уравнение, нужно исключить С из равенств:  Полученное соотношение
Полученное соотношение  и есть то дифференциальное уравнение, для которого и есть то дифференциальное уравнение, для которого  служит общим решением. Эту теорему примем без доказательств.
Пример. Пусть дана функция служит общим решением. Эту теорему примем без доказательств.
Пример. Пусть дана функция  , где С – произвольная постоянная. Требуется определить то дифференциальное уравнение, для которого она служит общим решением.
Решение. Используем теорему , где С – произвольная постоянная. Требуется определить то дифференциальное уравнение, для которого она служит общим решением.
Решение. Используем теорему   Искомым дифференциальным уравнением будет
Искомым дифференциальным уравнением будет  .
39. Однородные дифференциальные уравнения.
Функция f(x, y) называется однородной k-ого порядка, если существует такое число λ, что выполняется соотношение f(λx, λy) = xk f(x, y).
Дифференциальное уравнение y/ = f(x, y) называется однородным, если f(x, y) – однородная функция нулевого измерения.
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
Дифференциальное уравнение вида .
39. Однородные дифференциальные уравнения.
Функция f(x, y) называется однородной k-ого порядка, если существует такое число λ, что выполняется соотношение f(λx, λy) = xk f(x, y).
Дифференциальное уравнение y/ = f(x, y) называется однородным, если f(x, y) – однородная функция нулевого измерения.
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
Дифференциальное уравнение вида
 преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
 40. Уравнения, приводящиеся к однородным.
Уравнением, приводящимся к однородному, называется дифференциальное уравнение вида
40. Уравнения, приводящиеся к однородным.
Уравнением, приводящимся к однородному, называется дифференциальное уравнение вида
 Заменой u = y – y0, v = x – x0 это уравнение приводится к однородному уравнению
Заменой u = y – y0, v = x – x0 это уравнение приводится к однородному уравнению
 Здесь x0 и y0 — единственное решение линейной системы
Здесь x0 и y0 — единственное решение линейной системы
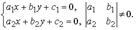
|
|
|
|
|
|
|
|
|
|
|
41 Уравнения 1-го порядка. Методы решений.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.190.187 (0.014 с.) |

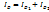

 двукратный інтеграл вычисляется по формуле
двукратный інтеграл вычисляется по формуле 
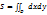 . (105). Если область определена в прямоугольной системе координат неравенством
. (105). Если область определена в прямоугольной системе координат неравенством 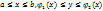 , то из (105) имеем
, то из (105) имеем  . (106). Если область D определена в полярных координатах неравенством
. (106). Если область D определена в полярных координатах неравенством 
 , то
, то  . (107)
. (107) , (108) где D есть проекция данной поверхности на плоскость хОу. Если поверхность задана уравнением x = f (y, z), то для вычисления площади имеем аналогичную формулу
, (108) где D есть проекция данной поверхности на плоскость хОу. Если поверхность задана уравнением x = f (y, z), то для вычисления площади имеем аналогичную формулу  . (109). Однако здесь D есть проекция поверхности на плоскость yOz. Аналогично, если поверхность задана уравнением y = f (x, z),
. (109). Однако здесь D есть проекция поверхности на плоскость yOz. Аналогично, если поверхность задана уравнением y = f (x, z),  (110) где D – проекция поверхности на плоскость xOz.
(110) где D – проекция поверхности на плоскость xOz. . (111) При z = f (x, y) < 0 объем цилиндрического тела вычисляется по формуле
. (111) При z = f (x, y) < 0 объем цилиндрического тела вычисляется по формуле 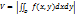 ,
, (скалярное поле на (в) трёхмерном пространстве, называемое иногда[1] пространственным полем).
(скалярное поле на (в) трёхмерном пространстве, называемое иногда[1] пространственным полем). (скалярное поле на (в) двумерном пространстве, называемое иногда[1] плоским полем).
(скалярное поле на (в) двумерном пространстве, называемое иногда[1] плоским полем).
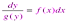






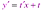 .
.



