
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые ряды. Основные теоремы о сходимостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть дана последовательность чисел а1,а2,а3,…,аn-1,an.Сумма этой числовой последовательности называется числовым рядом. Сумма конечного число членов ряда S1=a1, S2=a1+a2, S3=a1+a2+a3 … называется частичными суммами, если существует конечный предел Отбросим конечное число первых членов ряда и получим n-ый остаток ряда (rn). Теорема: для сходящегося ряда предел остатка равен 0 Теорема «Необходимый признак сходимости ряда»: общий член сходящегося ряда стремится к нулю Теорема: если ряд сходится и сумма его равна S, то ряд Теорема: если сходятся ряды
Положительные числовые ряды. Признак Коши и Деламбера. Положительным называется ряд, члены которого неотрицательны, то есть an≥0 Для того, чтобы положительный ряд сходился, необходимо и достаточно, чтобы последовательность частичных сумм была ограничена сверху Признак Деламбера: если члены последовательности ряда an таковы, что существует предел Признак Коши: если члены ряда an таковы, что существует предел
18. Знакочередующиеся числовые ряды. Абсолютная и условная сходимости. Ряд вида a1-a2+a3-a4+…+(-1)n+1an+… (1), где an≥0 называется знакочередующимся Признак Лейбница: Если члены ряда таковы, что: 1)каждый следующий, меньше предыдущего; 2) Рассмотрим ряды с членами произвольных знаков Если сходится ряд из модулей (2), то сходится ряд (1) Ряд (1) называют абсолютно-сходящимся, если ряд (2) сходится. Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) называют условно-сходящимся
Функциональные ряды. Равномерная сходимость функционального ряда.
Функциональным называется ряд, члены которого являются функциями u1(x)+u2(x)+…+un(x)+…= Областью определения ряда (1) называется область определения функции. Для каждой фиксированной точки х0 из области определения ряда получаем числовой ряд: Совокупность всех точек сходимости функционального ряда называется его областью сходимости. Частичные суммы ряда (1) тоже являются функциями. Суммой ряда называется функция, определенная в области сходимости и определенная следующим образом: Сходящиеся функциональные ряды обладают свойствами, аналогичными свойствам сходящихся числовых рядов. Признаки равномерной сходимости Признак сравнения Ряд 1. Ряд 2. Частным случаем является признак Вейерштрасса, когда Признак Дирихле Ряд 1. Последовательность действительнозначных функций 2. Частичные суммы Признак Абеля Ряд 1. Последовательность действительнозначных функций 2. Ряд
Степенные ряды Степенным называется функциональный ряд вида а0+а1х+а2х2+…+аnxn+…= Теорема Абеля: если ряд (1) сходится в т.х0, то он сходится абсолютно для всех х, таких что 0≤|x|≤|x0| О радиусе сходимости: пусть ряд (1) сходится не только при х0, но и не на всей числовой прямой, тогда существует положительное число R, такое что для всех х принадлежащем интервалу от –R до R ряд сходится, и для всех х не принадлежащих отрезку от –R до R расходится, число R называется радиусом сходимости степенного ряда. Радиус сходимости степенного ряда может быть вычислен по формулам: 1) 2) если существует предел Свойства: 1) Степенной ряд внутри интервала сходимости сходится равномерно 2) Суммой степенного ряда является функция, непрерывная внутри интервала сходимости
3) Пусть внутри интервала от –R до R степенной ряд сходится, тогда, для любого отрезка от 0 до х, принадлежащему этому интервалу, степенной ряд можно почленно интегрировать
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.13.203 (0.007 с.) |


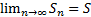 , то ряд называется сходящимся. Если последовательность частичных сумм не имеет предела, то ряд расходящийся и не имеет суммы.
, то ряд называется сходящимся. Если последовательность частичных сумм не имеет предела, то ряд расходящийся и не имеет суммы.
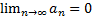 . Если же предел не стремится к нулю, то ряд расходится
. Если же предел не стремится к нулю, то ряд расходится (где с – некоторая постоянная) тоже сходится и сумма его равна cS.
(где с – некоторая постоянная) тоже сходится и сумма его равна cS. , и суммы их равны соответственно Sa и Sb, то ряд
, и суммы их равны соответственно Sa и Sb, то ряд  тоже сходится, причем сумма его равна Sa+Sb
тоже сходится, причем сумма его равна Sa+Sb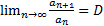 , то при D<1 ряд сходится, при D>1 ряд расходится, при D=1 требуется дополнительное исследование.
, то при D<1 ряд сходится, при D>1 ряд расходится, при D=1 требуется дополнительное исследование. , то при К<1 ряд сходится, при K>1 ряд расходится, при K=1 требуется дополнительное исследование.
, то при К<1 ряд сходится, при K>1 ряд расходится, при K=1 требуется дополнительное исследование. (2)
(2) (1)
(1) . Если этот ряд сходится, то х0 – точка сходимости ряда (1), если расходится, то х0 – точка расходимости ряда (1).
. Если этот ряд сходится, то х0 – точка сходимости ряда (1), если расходится, то х0 – точка расходимости ряда (1).
 сходится абсолютно и равномерно, если выполнены условия:
сходится абсолютно и равномерно, если выполнены условия: сходится равномерно.
сходится равномерно.
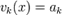 . Таким образом функциональный ряд ограничиваеся обычным. От него требуется обычная сходимость
. Таким образом функциональный ряд ограничиваеся обычным. От него требуется обычная сходимость сходится равномерно, если выполнены следующие условия:
сходится равномерно, если выполнены следующие условия: монотонна
монотонна  и
и 
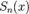 ряда
ряда 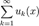 равномерно ограничены.
равномерно ограничены.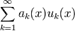 сходится равномерно, если выполнены следующие условия:
сходится равномерно, если выполнены следующие условия: .
. равномерно сходится.
равномерно сходится. (1)
(1)
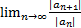 =D, то R=1/D
=D, то R=1/D


