
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признак Лейбница сходимости знакочередующегося ряда.Содержание книги
Поиск на нашем сайте Определение. Знакочередующийся ряд – ряд, у которого любые рядом стоящие члены имеют противоположные знаки. Теорема. Если в знакочередующемся ряде Доказательство. Рассмотрим сумму Запишем сумму в другом виде: Таким образом: S возрастает с возрастанием m и ограничена сверху. Теперь докажем, что «нечетные» частичные суммы также стремятся к пределу S. Для этого выражается Следовательно, ряд сходится. Замечание. Теорема Лейбница справедлива, еси неравенства
Абсолютная сходимость. Свойства абсолютно сходящихся рядов. Определение. Если ряд Теорема. Если ряд Доказательство. Запишем ряды почленно 1. 2. Пусть
По условию
Они имеют пределы
Замечание. Если ряд Для исследования абсолютной сходимости часто применяются признаки Коши и Даламбера, которые в этом случае имеют следующий вид. Теорема (признак Даламбера). Если в ряде с положительными членами 1.ряд АБСОЛЮТНО сходится, при l<1, 2. ряд расходится при l>1. Теорема (признак Коши). Если в ряде с положительными членами 1. ряд АБСОЛЮТНО сходится, при l<1, 2. ряд расходится при l>1. Примечание автора. Доказательств двух последних теорем приведены в ответах на предыдущие вопросы. Остаточный член формулы Тейлора в форме Лагранжа. Формула Тэйлора выглядит следующим образом:
Наша задача – оценить величину остаточного члена.
Рассмотрим вспомогательную функцию от t
Найдем производную и преобразуем ее: Заметим, что
Подставляя, получаем: Это – так называемая форма Лагранжа для остаточного члена. Так как Степенные ряды. Определение. Степенной ряд – функциональный ряд вида
Область сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку. Теорема Абеля. Если степенной ряд сходится (расходится) при некотором значении Доказательство. Так как, по предположению, числовой ряд сходится Перепишем ряд в следующем виде: Рассмотрим ряд из абсолютных величин его членов: Члены этого ряда меньше соответствующих членов ряда При Это значит, что ряды ___ Нетрудно будет доказать и второй случай (когда ряд расходящийся). Доказательство. Пусть в некоторой точке ___ Теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Если
Теорема (о строении области сходимости степенного ряда). Областью сходимости степенного ряда является интервал с центром в начале координат. Определение. Интервал сходимости степенного ряда – интервал от –R до +R, что для всякой точки х, лежащей внутри, ряд сходится, и притом абсолютно, а для точек вне интервала – ряд расходится. Число R – радиус сходимости ряда. Отметим, что у некоторых рядом интервал сходимости вырождается в точку (R=0), у других охватывает всю ось Ох Теорема. Степенной ряд Определение. Ряд называется мажорируемым, если каждый его член по абсолютной величине не больше соотвествующего члена некоторого сходящегося числового ряда с положительными членами. Доказательство. По условию Следовательно, ряд мажорируем на отрезке Следствие1. На всяком отрезке, целиком лежащем внутри интервала сходимости, сумма степенного ряда есть непрерывная функция. Это связано с тем, что члены ряда – непрерывные функции от х. Тогда и сумма этого ряда есть непрерывная функция. Следствие2. Если пределы интегрирования
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 члены таковы, что
члены таковы, что  и
и  то ряд сходится, его сумма положительна и не превосходит первого члена.
то ряд сходится, его сумма положительна и не превосходит первого члена. первых членов исходного ряда:
первых членов исходного ряда:  Так как
Так как  и возрастает с возрастанием
и возрастает с возрастанием 
 Каждая скобка здесь также положительна. В результате вычисления получим число, меньшее
Каждая скобка здесь также положительна. В результате вычисления получим число, меньшее  то есть
то есть 
 причем
причем 
 и аналогично записывается предел
и аналогично записывается предел 
 сходится, то говорят, что ряд
сходится, то говорят, что ряд  сходится абсолютно. Если
сходится абсолютно. Если 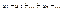

 -сумма первого ряда,
-сумма первого ряда,  -сумма второго ряда.
-сумма второго ряда.  -сумма всех положительных,
-сумма всех положительных,  - сумма абсолютных величин.
- сумма абсолютных величин.
 и
и  .
. . Ряд сходится.
. Ряд сходится.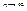 имеет предел, т.е.
имеет предел, т.е. 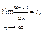 то:
то: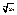 имеет предел
имеет предел  при
при 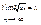 то:
то:

 остаточный член. Для тех значений х, которых остаточный член мал, многочлен дает приближенное значение функции f(x).
остаточный член. Для тех значений х, которых остаточный член мал, многочлен дает приближенное значение функции f(x). где Q – некоторая функция, подлежащая определению.
где Q – некоторая функция, подлежащая определению.



 и
и 


 заключено между х и а, то его можно представить как
заключено между х и а, то его можно представить как 

 где
где  - постоянные числа (коэффициенты ряда).
- постоянные числа (коэффициенты ряда). то он абсолютно сходится (расходится) при всяком значении х, для которого
то он абсолютно сходится (расходится) при всяком значении х, для которого 

 то общий член
то общий член  при
при  Это значит, что существует такое положительное число М, что все члены по абсолютной величине меньше М.
Это значит, что существует такое положительное число М, что все члены по абсолютной величине меньше М.


 и, следовательно, сходится. Отсюда сходится и
и, следовательно, сходится. Отсюда сходится и  ряд
ряд 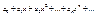 расходится. Тогда он будет расходиться в любой точке, удовлетворяющей условию
расходится. Тогда он будет расходиться в любой точке, удовлетворяющей условию 
 заполнен точками абсолютной сходимости и наоборот.
заполнен точками абсолютной сходимости и наоборот.
 целиком лежащем внутри интервала сходимости.
целиком лежащем внутри интервала сходимости. а потому ряд (с положительными членами) сходится. Но при
а потому ряд (с положительными членами) сходится. Но при  члены ряда по абсолютной величине не больше соответствующих членов ряда
члены ряда по абсолютной величине не больше соответствующих членов ряда 

 лежат внутри интервала сходимости, то интеграл от суммы ряда равен сумме интегралов от членов ряда. Так как область интегрирования можно заключить в отрезок
лежат внутри интервала сходимости, то интеграл от суммы ряда равен сумме интегралов от членов ряда. Так как область интегрирования можно заключить в отрезок 


