Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые ряды. Теоремы сравнения.Содержание книги
Поиск на нашем сайте
Определение. Числовой ряд – пара последовательностей и где числа - первый, второй…н-ный член ряда. - первой, второй…н-ной частичной суммой ряда. Теорема (признак сравнения). Если члены ряда Доказательство. Обозначим частичные суммы, как Так как второй ряд сходится, то существует предел его частичной суммы Так как члены ряда положительны, то Итак, мы доказали, что частичные суммы ограничены. Отсюда, они имеют предел Очевидно, что Аналогично: Если члены ряда Доказательство. Так как члены положительны, то частичная сумма ряда возрастает при возрастании n. Получаем Так как 24. Свойства сходящихся рядов. 1. Если ряд Переходя в этом равенстве к пределу при Т.о.,ряд
Теорема (признак Коши). Теорема. Если в ряде с положительными членами 1. ряд сходится, при l<1, 2. ряд расходится при l>1. Доказательство. 1. Пусть l<1. Рассмотрим q, при котором Начиная с некоторого N ( Отсюда следует, что Рассмотрим 2 ряда:
Второй ряд сходится, так как его члены образуют убывающую геометрическую прогрессию. 2. Пусть l>1. С некоторого n=N будет иметь место неравенство Ряд расходится, так как его общий член не стремится к нулю (все члены больше 1). Замечание. Как и в признаке Даламбера случай
27. Теорема (признак Даламбера). Теорема. Если в ряде с положительными членами 1.ряд сходится, при l<1, 2. ряд расходится при l>1, 3. теорема не дает ответа при l=1. Доказательство. 1. Пусть l<1. Рассмотрим q, при котором Начиная с некоторого N ( Действительно, так как величина Начиная с любого N, получаем систему неравенств:
Складывая таким образом члены последовательности, приходим к выводу, что перед нами геометрическая прогрессия со знаменателем 2. Пусть l>1. Из равенства Замечание1. Ряд будет расходиться и том случае, когда Замечание2. Если
Интегральный признак сходимости. Теорема. Пусть члены ряда Доказательство. Примечание автора. Необходимы 2 графические иллюстрации. Из первого графика очевидно Из второго - Рассмотрим первый случай (сходится). Предположим, что интеграл сходится
Рассмотрим второй случай (расходится). Предположим, что Замечание. Ни признак Даламбера, ни признак Коши не решают вопроса о сходимости этого ряда, так как предел равен единице.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.221.45 (0.01 с.) |

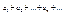 не больше соответствующих членов ряда
не больше соответствующих членов ряда 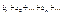 то есть
то есть 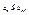 и второй ряд сходится, то сходится и первый.
и второй ряд сходится, то сходится и первый.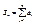 и
и 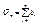 Из условия следует, что
Из условия следует, что 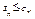

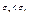
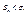

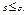
 и второй ряд расходится, то расходится и первый.
и второй ряд расходится, то расходится и первый.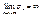
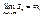 то есть ряд расходится.
то есть ряд расходится.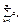 сходится, то
сходится, то  2. Теорема1. Если сходится ряд, получившийся из данного ряда
2. Теорема1. Если сходится ряд, получившийся из данного ряда 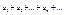 отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов, т.е. на сх. ряда не влияет отбрасывание конечного числа его членов. Доказательство. Пусть
отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов, т.е. на сх. ряда не влияет отбрасывание конечного числа его членов. Доказательство. Пусть 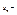 сумма n первых членов ряда.
сумма n первых членов ряда. 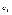 -сумма k отброшенных членов,
-сумма k отброшенных членов, 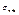 - сумма членов ряда, входящих в сумму и не входящих в
- сумма членов ряда, входящих в сумму и не входящих в  Тогда имеем: Тогда имеем:
Тогда имеем: Тогда имеем: 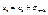 ,где
,где 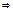 , что если
, что если 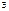
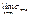 ,то
,то  , если
, если 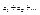 сходится и его сумма =s, то ряд
сходится и его сумма =s, то ряд 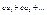 , где с - какое-либо фиксированное число, также сходится и его сумма=cs. Доказательство. Обозначим n-ую частичную сумму ряда
, где с - какое-либо фиксированное число, также сходится и его сумма=cs. Доказательство. Обозначим n-ую частичную сумму ряда  , а ряда
, а ряда 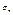 .Тогда
.Тогда 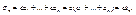 Отсюда ясно, что предел n-й частичной суммы ряда
Отсюда ясно, что предел n-й частичной суммы ряда  Следовательно, ряд
Следовательно, ряд 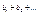 сходятся и их суммы равны
сходятся и их суммы равны 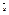 и
и  , то ряды
, то ряды 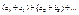 и
и 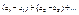 также сходятся и их суммы. Они равны
также сходятся и их суммы. Они равны 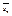 и
и 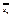 , получим:
, получим: 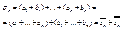
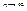 , получим
, получим 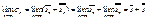 .
. . Ряды
. Ряды 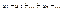 величина
величина 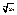 имеет предел
имеет предел  при
при 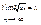 то:
то: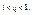
 ) выполняется неравенство
) выполняется неравенство 
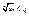 или
или 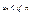 для всех
для всех 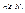
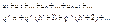
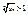 или
или 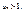
 требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся ряды.
требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся ряды.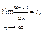 то:
то: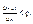
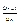 стремится к
стремится к 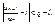
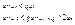
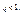
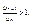
 Это означает, что члены ряда возрастают, поэтому ряд расходится.
Это означает, что члены ряда возрастают, поэтому ряд расходится.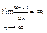 Это следует из неравенства
Это следует из неравенства 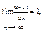 но отношение
но отношение 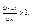 то
то 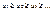 и пусть f(x) – такая непрерывная невозрастающая функция, что
и пусть f(x) – такая непрерывная невозрастающая функция, что  Тогда если несобственный интеграл
Тогда если несобственный интеграл 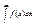 сходится/расходится, то сходится/расходится и ряд.
сходится/расходится, то сходится/расходится и ряд.
 откуда
откуда 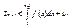

 Частичная сумма
Частичная сумма 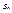 остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены положительны. Следовательно, ряд сходится.
остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены положительны. Следовательно, ряд сходится. Это значит, что при возрастании n неограниченно возрастает интеграл
Это значит, что при возрастании n неограниченно возрастает интеграл  Тогда в силу
Тогда в силу