
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Универсальная тригонометрическая замена.Содержание книги
Поиск на нашем сайте
Применяется для Выражаем Примечание. Если тригонометрические функции в четных степенях, проще делать замену:
Интегрирование тригонометрических функций.
а. m-нечетное => б. n-нечетное => в. m и n-четные => формулы понижения степени.
Несобственные интегралы от неограниченной функции. Свойства. Определение. Если существует конечный предел Пусть Интеграл от функции, терпящей разрыв в точке c, определяется следующим образом: Если предел, стоящий справа, существует, то интеграл несобственный сходящийся, иначе расходящийся. Если функция имеет разры в левом конце отрезка Если разрыв в некоторой точке Замечание. Если функция. определенная на отрезке Для определения сходимости несобственных интегралов от различных функций могут быть применены теоремы, аналогичные теоремам для оценки интегралов с бесконечными пределами. Теорема1. Если на отрезке Теорема2. Если на отрезке Теорема3. Если _________________________________________ В качестве функции, с которыми сравнивают функции под знаком интеграла, часто берут
Интеграл, зависящий от параметра. Определение. Функция При изменении параметра меняется значение интеграла. Это и доказывает, что интеграл, зависящий от параметра – функция. Доказательство. Предположим, что А это и есть Или все это можно представить в другой форме – формула Лейбница Гамма-функция. Определение. Функция Интеграл, определяющий гамма-функцию, несобственный по бесконечному промежутку. При Теорема. Гамма-функция определена и непрерывна для любых Доказательство. Разобьем интеграл на сумму двух интегралов: Рассмотрим Функция Рассмотрим При Функция ____ Имеют место следующие утверждения: 1. При любом неотрицательном х Доказывается интегрированием по частям. 2. 3. При любом натуральном n 4.
Нахождение площади в декартовых координатах. Если на отрезке [a,b] функция Если Если функция меняет знак на отрезке, то интеграл по всему отрезку разбиваем на сумму интегралов по частичным отрезкам. Примечание автора. Обязательны 2 графические иллюстрации. Если нужно вычислить площадь области, ограниченной кривыми Кривая может быть задана уравнениями в параметрической форме
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.24 (0.006 с.) |


 затем через тригонометрические формулы выражаем значения синуса и косинуса:
затем через тригонометрические формулы выражаем значения синуса и косинуса: 






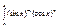
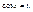
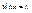
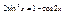

 то этот предел называют несобственным интегралом от функции на промежутке
то этот предел называют несобственным интегралом от функции на промежутке  и обозначают так
и обозначают так 
 определена и непрерывна при
определена и непрерывна при  а при
а при 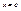 функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об интеграле
функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об интеграле  как о пределе интегральных сумм, так как
как о пределе интегральных сумм, так как  поэтому предел может и не существовать.
поэтому предел может и не существовать.
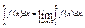
 (внутри отрезка), то полагают
(внутри отрезка), то полагают  (если оба стоящих справа интеграла существуют).
(если оба стоящих справа интеграла существуют).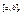 имеет внутри отрезка конечное число точек разрыва
имеет внутри отрезка конечное число точек разрыва  то интеграл определяется так:
то интеграл определяется так:  (если каждый из интегралов в правой части сходится). Если же хотя бы один из них расходится, то
(если каждый из интегралов в правой части сходится). Если же хотя бы один из них расходится, то  - расходящийся.
- расходящийся. функции
функции 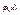 разрывны в точке с, причем во всех точках выполняется
разрывны в точке с, причем во всех точках выполняется  и если
и если 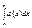 сходится, то сходится и
сходится, то сходится и 
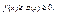 и если
и если 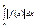 от абсолютной величины этой функции сходится, то сходится также интеграл
от абсолютной величины этой функции сходится, то сходится также интеграл 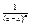 (при
(при  интеграл сходится, при
интеграл сходится, при  расходится).
расходится). называется интегралом, зависящим от параметра
называется интегралом, зависящим от параметра 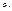
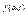 и
и  есть непрерывные функции. Найдем производную по параметру х.
есть непрерывные функции. Найдем производную по параметру х. 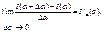

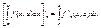
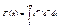 на промежутке
на промежутке 
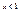 подынтегральная функция терпит разрыв при
подынтегральная функция терпит разрыв при 


 Для любого
Для любого 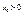 существует
существует  что
что  Тогда для любого
Тогда для любого 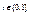 и для любого x из окрестности
и для любого x из окрестности 
 интегрируема на этом отрезке. Следовательно, для любого
интегрируема на этом отрезке. Следовательно, для любого  сходится и функция
сходится и функция 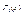 непрерывна при любом
непрерывна при любом 
 Из формулы Тэйлора с остаточным членом в форме Лагранжа:
Из формулы Тэйлора с остаточным членом в форме Лагранжа: 

 для любого
для любого  Подберем n так, чтобы
Подберем n так, чтобы  Значит при
Значит при  справедливо неравенство
справедливо неравенство 
 интегрируема на отрезке. Следовательно, при любом
интегрируема на отрезке. Следовательно, при любом 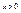 интеграл сходится и функция непрерывна при любом
интеграл сходится и функция непрерывна при любом 


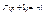
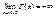

 то площадь криволинейной трапеции, ограниченной кривой
то площадь криволинейной трапеции, ограниченной кривой  осью Ох и прямыми х=а, х=b.
осью Ох и прямыми х=а, х=b. 



 х=а, х=b, будем иметь:
х=а, х=b, будем иметь: 





