
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральный синус. Свойства.Содержание книги
Поиск на нашем сайте
Определяется формулой: Подынтегральная функция непрерывна, если доопределить ее так: Так как функция «синус» нечетная, несложно понять, сто и интегральный синус – тоже нечетная. Взяв вторую производную, Следовательно, в точках, где k>0 и четные И k<0 и нечетные – минимумы функции. где k<0 и четные И k>0 и нечетные – максимумы. Примечание автора. Обязательна графическая иллюстрация. Интегральный логарифм. Специальная функция, определяемая интегралом Он был введен в матем. анализ Эйлером. Известно, что для больших положительных функций, растет как Интегрирование рациональных дробей. Требуется вычислить интеграл от рациональной дроби. Правильная или неправильная? Если неправильная, представляем ее в виде многочлена М(х) и правильной дроби Правильную представляем в виде суммы простейших дробей. Интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких простейших дробей. Возможны 4 случая: 1.Корни знаменателя действительны и различны.
2. Корни знаменателя действительные, причем некоторые из них кратные:
После данного преобразования дроби интегрируются. 3. Корни знаменателя – комплексные, различные.
Разложение и последующее интегрирование аналогично второму случаю. 4. Корни знаменателя – комплексные кратные.
Разложение и последующее интегрирование аналогично трем предыдущим случаем. Несобственные интегралы по неограниченному промежутку. Теоремы сравнения. Определение. Если существует конечный предел Говорят, что в этом случае Во многих случаях достаточно установить сходится или расходится данный интеграл и оценить его значение. Для этого применяют теоремы сравнения. Теорема1. Пусть сходятся или расходятся одновременно. Если сходятся, то справделиво равенство Доказательство. Следует из аддитивности определенного интеграла по промежутку. Теорема2. Если F – первообразная к функции f на отрезке Определение. Если интеграл Последний интеграл – абсолютно сходящийся.
Формула прямоугольников Дана непрерывная функция на отрезке [a,b]. Требуется вычислить определенный интеграл Составим суммы:
Каждая из этих сумм – интегральная сумма для f(x) на отрезке [a,b] и поэтому приближенно вычисляет интеграл.
Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) заменена суммой площадей заштрихованных прямоугольников. Примечание. Чем больше число шагов n, тем незначительнее ошибка при вычислении интеграла.
Формула трапеций. Эта формула является более точной по сравнению с формулой прямоугольников, что объясняется заменой ступенчатой линии на вписанную ломаную.
y1 у2 уn
a x1 x2 b x
Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Площади вписанных трапеций вычисляются по формулам:
После приведения подобных слагаемых получаем формулу трапеций: Число n выбирается произвольно. Чем больше оно будет, тем меньше будет шаг
Выбор числа шагов при заданной точности. Вычислить приближенное значение с заданной точностью означает, что выполняется неравенство: При вычислениях интеграла погрешность учитывается следующим образом:
Методы рационализации. Подстановка Эйлера. Рассмотрим интеграл Первая подстановка Эйлера. Если a>0, то полагаем:
Вторая подстановка Эйлера. Если с>0, то полагаем: Третья подстановка Эйлера. Пусть Замечание1. Третья подстановка Э.применима не только при а<0,но и при a>0-лишь бы многочлен Замечание 2. Заметим, что для приведения интеграла
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 764; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.70.64 (0.008 с.) |



 и подставив значение
и подставив значение  получаем:
получаем: 
 Этот интеграл не выражается в конечной форме через элементарные функции. Если
Этот интеграл не выражается в конечной форме через элементарные функции. Если  то интеграл понимается в смысле
то интеграл понимается в смысле 



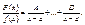
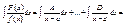





 то этот предел называют несобственным интегралом от функции на промежутке
то этот предел называют несобственным интегралом от функции на промежутке  и обозначают так
и обозначают так 
 интеграл существует/сходится. Если
интеграл существует/сходится. Если  при
при 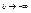 не имеет конечного предела, то говорят что он расходится/не существует.
не имеет конечного предела, то говорят что он расходится/не существует. тогда несобственные интегралы
тогда несобственные интегралы 

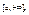 то остается справедливой формула Ньютона-Лейбница в виде
то остается справедливой формула Ньютона-Лейбница в виде 
 сходится, то сходится и
сходится, то сходится и 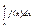 Разделим отрезок на n равных частей длины
Разделим отрезок на n равных частей длины  точками
точками 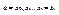
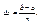 Обозначим через
Обозначим через  значения f(x) в этих точках,т.е.
значения f(x) в этих точках,т.е. 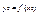


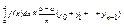 или
или 

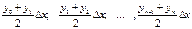


 тем с большей точностью вычисляется значение интеграла.
тем с большей точностью вычисляется значение интеграла.
 - приближенное значение,
- приближенное значение,  - заданная погрешность.
- заданная погрешность. М – наибольшее значение модуля второй производной на заданном отрезке.
М – наибольшее значение модуля второй производной на заданном отрезке. где
где 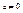 .Такой интеграл приводится к интегралу от рациональной функции нового переменного с помощью следующих подстановок Эйлера.
.Такой интеграл приводится к интегралу от рациональной функции нового переменного с помощью следующих подстановок Эйлера. Возьмем для определенности знак +. Получаем
Возьмем для определенности знак +. Получаем 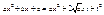 , откуда
, откуда 

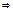
 , т.е.
, т.е. 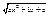 оказывается рациональной функцией от t. Так как
оказывается рациональной функцией от t. Так как  ,x,dx выражаются рационально через t,то
,x,dx выражаются рационально через t,то  преобразуется в интеграл от рациональной функции от t.
преобразуется в интеграл от рациональной функции от t. Берем для определенности знак +.
Берем для определенности знак +.  . Отсюда
. Отсюда  .Т.к. dx и
.Т.к. dx и  и
и 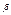 – действительные корни трехчлена
– действительные корни трехчлена  .Полагаем:
.Полагаем:  Так как
Так как 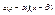 ,то
,то 
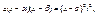
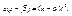 Отсюда
Отсюда  .Т.к. dx и
.Т.к. dx и  ,то корни трехчлена действительны, и
,то корни трехчлена действительны, и  , то в этом случае
, то в этом случае  и,
и, 


