
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональные последовательности и ряды. Равномерная сходимость. Критерий Коши.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть на числовой прямой Е1 или в т - мерном евклидовом пр-ве Ет задано некоторое множество { x }. Если каждому п из натурального ряда чисел 1, 2,......, п,... ставится в соответствие по определенному закону некоторая функция fп (х), определенная на множестве { x }, то множество занумерованных функций f 1 (x), f 2 (x),..., fn (x), ... называется функциональной послед-стью. fn (x) ̶ члены или элементы послед-сти, множество { x } ̶ область определения послед-сти. Пусть { ип (х)} - функц. послед-сть, { х } - ее область определения. Формально написанная сумма
бесконечного числа членов этой функц. послед-сти - функциональный ряд. ип (х) ̶ члены ряда, { х } ̶ область определения этого ряда. Сумма первых п членов ряда (1) ̶ n ̶ я частичная сумма. Изучение функц. рядов его частичных сумм и, наоборот, каждой функц. послед-сти (2) однозначно соответствует функц. ряд (1) с членами u 1(х)= S 1(x), ип (х) = Sп (х) ̶ Sп ̶ 1 (х)при n ≥ 2. Пусть { х } пр-ва Ет - область определения функц. послед-сти (функц. ряда). Фиксируем Пусть { х } - область сходимости функц. послед-сти { fп (х)}. Совокупность пределов, взятых для всех точек х Если { х } - область сходимости функц. ряда (2),то на { х } определена функция S (х), являющаяся предельной функцией послед-сти частичных сумм этого ряда и называемая его суммой. Пусть функц. послед-сть f 1 (x), f 2 (x),..., fn (x), ... (3) сходится на { х }пр-ва Ет к предельной f (x). О1. Послед-сть (3) сходится к функции f (х) равномерно на { х }, если для О2. Функц. ряд называется равномерно сходящимся на { х } к сумме S (х), если послед-сть { Sn (x)} его частичных сумм сходится равномерно на множестве { х } к предельной функции S (х). Т1 (критерий Коши). Чтобы функц. послед-сть { fn (x)} равномерно на { х } сходилась к некоторой предельной функции, необходимо и достаточно, чтобы для для всех номеров п (п ≥ N (ε)), всех р Т2. Чтобы функц. ряд
равномерно на { х } сходился к некоторой сумме, необходимо и достаточно, чтобы для
для всех номеров п (п ≥ N (ε)), всех р (Т2 - следствие Т1, т.к. в левой части (7) под знаком модуля стоит разность Sп+p (х) ̶ Sп (х)частичных сумм с номерами п+р и п функц. ряда (6)). Док-во Т 1. Необх-сть. Пусть
справедливо для всех п (п ≥ N (ε)) и для всех х Если р -
Так как модуль суммы двух величин не превосходит суммы их модулей, то из (8) и (9):
(для всех п (п ≥ N (ε)), всех р Дост-сть. Пусть для Фиксировав
11. Признаки равномерной сходимости функциональных рядов (два признака Абеля, признаки Дирихле ̶ Абеля, Вейерштрасса). О1. Функц. послед-сть f 1 (x), f 2 (x),..., fn (x), ... сходится к функции f (х) равномерно на множестве { х }, если для
О2. Функц. ряд называется равномерно сходящимся на множестве { х } к сумме S (х), если послед-сть { Sn (x)} его частичных сумм сходится равномерно на { х } к предельной функции S (х). Т1. (признак Вейерштрасса). Если функц. ряд
определен на множестве { х } пр-ва Ет и если
такой, что для всех х
то функц. ряд (1) сходится равномерно на { х }. Док-во. Фиксируем
для всех п (п ≥ N (ε)) и р
(для всех п (п ≥ N (ε)), всех р О3. Функц. послед-сть { fn (x)} называется равномерно ограниченной на { x }, если О4. Функц. послед-сть { vn (x)} называется послед-стью, обладающей на { x } равномерно ограниченным изменением, если функц. ряд
сходится равномерно на { x }. З1. Всякая послед-сть, обладающая на { x } равномерно ограниченным изменением, сходится равномерно на { х } к некоторой предельной функции. Из равномерной на { x } сходимости ряда (5) и из критерия Коши** => равномерная на { x } сходимость ряда
n- я частичная сумма которого: Т2 (1 ̶ й признак Абеля). Если функц. ряд
обладает равномерно ограниченной на { x } послед-стью частичных сумм, а функц. послед-сть { vn (x)} обладает равномерно ограниченным на { x } изменением и имеет предельную функцию, ≡ 0, то на { x } сходится равномерно функц. ряд
Док ̶ во. Послед-сть Sп (х)частичных сумм ряда (1) равномерно ограничена => Фиксируем
и т.к. модуль суммы не превосходит сумму модулей:
Учитывая, что для всех п и всех х из { x }
=> и из (7) и (8) для всех п > N, всех р
=> ряд (9) сходится равномерно на { x } (по Т**). З2. На равномерную на { x } сходимость функц. ряда не влияет отбрасывание З3. Если функц. ряд сходится равномерно на { x }, то для По критерию Коши равномерной на { x } сходимости исходного функц. ряда для Под знаком модуля в (10) стоит частичная сумма Т3 (2 ̶ й признак Абеля). Если функц. ряд (1) сходится равномерно на { x }, а функц. послед-сть { vn (x)} обладает равномерно на { x } ограниченным изменением и является равномерно ограниченной на { x }, то функц. ряд (6) сходится равномерно на { x }. Док- во. { vn (x)}равномерно ограничена на { x } =>
Фиксируем
Отбросим у рядов (1), (5) и (6) 1-е N членов. (Это в силу З2 не влияет на их равномерную на { x } сходимость). В силу критерия Коши равномерной на { х }сходимости ряда (5) (с отброшенными 1-ми N членами) для M > 0
В силу тождества Абеля для всех n и р и всех х из { x }:
=> из (11), (11’) и (11’’) для всех п ≥ N 1, всех р
=> по критерию Коши равномерная на { x } сходимость функц. ряда (6). Сл. (признак Дирихле - Абеля). Если функц. ряд (1) обладает равномерно ограниченной на { x } послед-стью частичных сумм, а функц. послед-сть { vn (x)} не возрастает в каждой точке { x } и равномерно на этом множестве сходится к 0, то функц. ряд (6) сходится равномерно на { x }. Т.к. { vn (x)}не возрастает в каждой точке { x } и
*: Чтобы ряд **: Чтобы функц. ряд ***: Чтобы функц. послед-сть { fn (x)} равномерно на { х } сходилась к некоторой предельной функции, необходимо и достаточно, чтобы для
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 изучению функц. послед-стей, ибо каждому функц. ряду (1) однозначно соответствует функц. послед-сть S 1(x), S 2(x), …, Sn (x), … (2)
изучению функц. послед-стей, ибо каждому функц. ряду (1) однозначно соответствует функц. послед-сть S 1(x), S 2(x), …, Sn (x), … (2) точку x 0 = (x 1º, x 2º, …, хт º)
точку x 0 = (x 1º, x 2º, …, хт º)  { х }и рассмотрим все члены функц. послед-сти (функц. ряда) в х 0 => получим числовую послед-сть (числовой ряд). Если эта числовая послед-сть (числовой ряд) сходится, то функц. послед-сть (функц. ряд) сходится в точке х 0. Множество всех точек х 0 ,в которых сходится данная функц. послед-сть (функц. ряд), называется областью сходимости этой послед-сти (ряда).
{ х }и рассмотрим все члены функц. послед-сти (функц. ряда) в х 0 => получим числовую послед-сть (числовой ряд). Если эта числовая послед-сть (числовой ряд) сходится, то функц. послед-сть (функц. ряд) сходится в точке х 0. Множество всех точек х 0 ,в которых сходится данная функц. послед-сть (функц. ряд), называется областью сходимости этой послед-сти (ряда).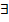 N = N (ε): для всех п (п ≥ N (ε)) и для всех точек х
N = N (ε): для всех п (п ≥ N (ε)) и для всех точек х 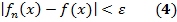
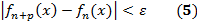
 и всех точек х
и всех точек х 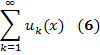

 на { х } => фиксировав
на { х } => фиксировав 
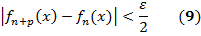

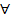 х
х  =>
=> 



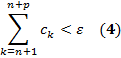

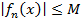


 =>
=>  , где
, где  , S (х) ̶ сумма ряда (5').
, S (х) ̶ сумма ряда (5').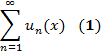

 .
. и ряд (5) равномерно на { x } сходится):
и ряд (5) равномерно на { x } сходится):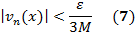

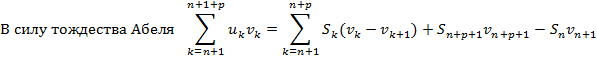



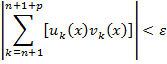
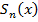 функц. ряда, начиная с п ≥ N, изменяются на одну и ту же функцию (= сумме первых N членов) => разность
функц. ряда, начиная с п ≥ N, изменяются на одну и ту же функцию (= сумме первых N членов) => разность  в критерии Коши (Т** и Т***) при
в критерии Коши (Т** и Т***) при 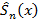 функц. ряда, получающегося после отбрасывания этих членов, для всех х из { x }, будут удовлетворять неравенству
функц. ряда, получающегося после отбрасывания этих членов, для всех х из { x }, будут удовлетворять неравенству 
 N = N (ε): для всех х из { x } и всех р
N = N (ε): для всех х из { x } и всех р 
 с номером р функц. ряда, полученного после отбрасывания 1-х N членов у исходного ряда => (10) переходит в (9).
с номером р функц. ряда, полученного после отбрасывания 1-х N членов у исходного ряда => (10) переходит в (9).

 р
р 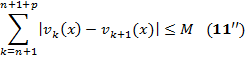


 => { vn (x)}обладает на { x } равномерно ограниченным изменением =>
=> { vn (x)}обладает на { x } равномерно ограниченным изменением => 
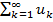 сходился, необходимо и достаточно, чтобы для
сходился, необходимо и достаточно, чтобы для  :
: 
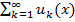 равномерно на { х } сходился к некоторой сумме, необходимо и достаточно, чтобы для
равномерно на { х } сходился к некоторой сумме, необходимо и достаточно, чтобы для  для всех п (п ≥ N (ε)), всех р
для всех п (п ≥ N (ε)), всех р  для всех п (п ≥ N (ε)), всех р
для всех п (п ≥ N (ε)), всех р 


