
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимое условие сходимости двойного ряда. Связь между сходимостью двойного ряда и повторного ряда. Критерий сходимости двойного ряда с неотрицательными членами.Содержание книги
Поиск на нашем сайте
Рассмотрим счетное множество бесконечных числовых послед-стей
…
… Просуммировав каждую строку матрицы отдельно, получим бесконечную послед-сть рядов вида
Просуммировав эту послед-сть, получим повторный ряд
Другой повторный ряд
получится, если сначала просуммировать отдельно каждый столбец матрицы (1), а затем взять сумму элементов полученной при этом послед-сти. О1. Повторный ряд (3) называется сходящимся, если сходится каждый из рядов (2) и если сходится ряд О2. Повторный ряд (4) называется сходящимся, если сходится каждый из рядов
и если сходится ряд С матрицей (1) связывают еще двойной ряд
О3. Двойной ряд (6) называется сходящимся, если при независимом стремлении двух индексов т и п к бесконечности
прямоугольных частичных сумм
При этом указанный предел (7) называют суммой двойного ряда (6). Из этого определения => если двойной ряд (6) получен перемножением членов двух сходящихся «одинарных» рядов
т. е. если члены двойного ряда (6) равны Из (8) => для Последнее равенство означает Утв. Необходимым условием сходимости двойного ряда (6) является стремление к 0 его общего члена, т. е. существование при независимом стремлении т и п к бесконечности равного 0 предела
Т1. Если сходится двойной ряд (6) и если сходятся все ряды по строкам (2), то сходится и повторный ряд (3), причем к этой же сумме, к которой сходится двойной ряд (6). Док ̶ во. Перейти при фиксированном т к пределу при п→∞ в (8) и учесть сходимость ряда (2) к сумме
Из (10) => сумма повторного ряда (3) - это повторный предел при т→∞ правой части (10):
Пусть
Т2. Если все элементы матрицы (1) неотрицательны, то для сходимости составленного из этой матрицы двойного ряда (6) необходимо и достаточно, чтобы его частичные суммы (8) были ограничены. Док ̶ во. Необх-сть очевидна. Дост-сть. Из ограниченности
По определению точной верхней грани для Для всех т и п: т ≥ т 0, п ≥ n 0, из неотрицательности элементов =>
8. Абсолютная сходимость двойного ряда. Взаимосвязь между сходимостью четырех рядов: повторных, двойного и «одинарного». Рассмотрим счетное множество бесконечных числовых послед-стей
…
… Просуммировав каждую строку матрицы отдельно, получим бесконечную послед-сть рядов вида
Просуммировав эту послед-сть, получим повторный ряд
Другой повторный ряд (4) получится, если сначала просуммировать отдельно каждый столбец матрицы (1), а затем взять сумму элементов полученной при этом послед-сти. О1. Повторный ряд (3) называется сходящимся, если сходится каждый из рядов (2) и если сходится ряд О2. Повторный ряд (4) называется сходящимся, если сходится каждый из рядов
и если сходится ряд С матрицей (1) связывают еще двойной ряд
О3. Двойной ряд (6) называется сходящимся, если при независимом стремлении индексов т и п к бесконечности
прямоугольных частичных сумм
При этом указанный предел (7) называют суммой двойного ряда (6). Из этого определения => если двойной ряд (6) получен перемножением членов двух сходящихся «одинарных» рядов
т. е. если члены двойного ряда (6) равны О4. Двойной ряд (6) называется абсолютно сходящимся, если сходится двойной ряд, составленный из модулей элементов матрицы (1):
Т1. Если сходится двойной ряд из модулей (6'), то сходится и двойной ряд (6). Док ̶ во. Положим
Здесь
=> эти ряды сходятся по Т**. Обозначим их суммы Р и Q. Из (10) ряд (6) сходится к Р ̶ Q. •
Обычный ряд, его члены - занумерованные в Т2. Рассмотрим 4 ряда: два повторных ряда (3) и (4), двойной ряд (6) и ряд вида (11). Если хотя бы один из этих 4- х рядов сходится при замене его членов их абсолютными величинами, то все 4 ряда сходятся и имеют одну и ту же сумму.
Док-во. 1) док-во сходимости; для повторных рядов (3) и (4) рассуждения аналогичны (только меняются ролями 1-й и 2-й индексы) => рассматриваем только ряд (3). I) док-во, что из сходимости повторного ряда (3), у которого все члены заменены их модулями => абсолютная сходимость ряда (11). Пусть
Если получающегося при замене членов ряда (11) их модулями, то можно найти столь большие т и п, что все члены ряда (11), входящие в его частичную сумму с номером r, будут содержаться в первых т строках и первых п столбцах матрицы (1) = > в силу (12): II) док-во, что из абсолютной сходимости ряда (3) => абсолютная сходимость двойного ряда (6). Пусть ряд (11') сходится => по Т*** послед-сть его частичных сумм { III) док-во, что из абсолютной сходимости ряда (6) => сходимость повторного ряда (3), у которого все члены заменены их модулями. Пусть сходится ряд (6') => при
имеет ограниченную послед-сть частичных сумм => каждый из рядов (13) сходится => по Т* сходится повторный ряд из модулей (3'). 2) док-во совпадения сумм рядов (3), (6) и (13). Пусть S - сумма двойного ряда (6) => сумма ряда (13) равна S, т.к. в силу абсолютной сходимости этого ряда его сумма не меняется при изменении порядка следования его членов и этот порядок можно изменить так, что частичные суммы после изменения порядка будут содержать в качестве подмножества частичные суммы Sтп двойного ряда (13). Из сходимости рядов (13) => сходимость рядов (2) => по Т* сумма повторного ряда (3) также равна S. -------------------------------------------------------------------------------------------------------------------------- *: Если сходится двойной ряд (6) и если сходятся все ряды по строкам (2), то сходится и повторный ряд (3), причем к этой же сумме, к которой сходится двойной ряд (6). **: Если все элементы матрицы (1) неотрицательны, то для сходимости составленного из этой матрицы двойного ряда (6) необходимо и достаточно, чтобы его частичные суммы (8) были ограничены. ***: Чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы послед-сть частичных сумм этого ряда была ограничена.
9. Обобщенные методы суммирования расходящихся рядов (Чезаро и Пуассона ̶ Абеля).
Сумма (1) ̶ числовой ряд, иk ̶ члены ряда (1). п - я частичная суммой ряда:
О. Ряд (1) называется сходящимся, если сходится послед-сть { Sп } частичных сумм (2) этого ряда. При этом предел S указанной последовательности { Sп } называется суммой ряда (1):
Ряд, сходящийся в обычном смысле и имеющий обычную сумму S, должен иметь обобщенную сумму, и притом также равную S. Метод суммирования, обладающий указанным свойством, называется регулярным. Понятие обобщенной суммы подчиним условию: если ряд
где А и В ̶
Метод Чезаро (метод средних арифметических). Ряд (1) суммируем методом Чезаро, если
Предел (3) называется обобщенной в смысле Чезаро суммой ряда (1). Линейность метода суммирования Чезаро очевидна. Его регулярность вытекает из Л*, т.к. если { Метод Пуассона - Абеля. По ряду (1) составим степенной ряд
Если он сходится для
в точке х = 1, то ряд (1) суммируем методом Пуассона - Абеля. Это предельное значение называется суммой ряда (1) в смысле Пуассона - Абеля. Линейность метода Пуассона - Абеля очевидна. Докажем регулярность. Пусть ряд (1) сходится в обычном смысле и его сумма = S. Надо доказать: 1) ряд (4) сходится для 1). (1) сходится => то послед-сть его членов бесконечно малая => и ограниченная => | x |<1 => ряд 2) Пусть
Вычтем (5) из тождества:
Обозначая через
Надо доказать, что для
Остается доказать, что для х, достаточно близких к 1,
но это очевидно, т.к. сумма в последнем неравенстве ограничена. Регулярность метода доказана. *: Если послед-сть { ап } сходится к пределу l, то к тому же пределу сходится и послед-сть σп = (а 1+ a 2 + … +ап) / п средних арифметических чисел а 1, а 2 ,...,ап. **: Т сравнения. Пусть З. Т справедлива, если ***: Пусть { иk } и { vk } ̶ 2
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 827; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.62.46 (0.012 с.) |

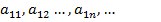
 (1)
(1)



 , в котором
, в котором  обозначает сумму k ̶ го ряда (2).
обозначает сумму k ̶ го ряда (2).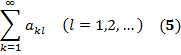
 , в котором
, в котором  обозначает сумму ̶ го ряда (5).
обозначает сумму ̶ го ряда (5).
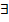 конечный предел
конечный предел
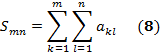

 ,то этот двойной ряд сходится, а его сумма равна произведению сумм рядов (9).
,то этот двойной ряд сходится, а его сумма равна произведению сумм рядов (9). т ≥ 2, п ≥ 2:
т ≥ 2, п ≥ 2: 

 :
:

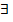 т 0 и n 0: при т ≥ т 0, п ≥ n 0справедливо
т 0 и n 0: при т ≥ т 0, п ≥ n 0справедливо  => т.к. для
=> т.к. для 
 => существование точной верхней грани этого множества S:
=> существование точной верхней грани этого множества S:
 :
: 
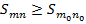 => и из (11):
=> и из (11): для всех т и п при т ≥ т 0, п ≥ n 0 =>
для всех т и п при т ≥ т 0, п ≥ n 0 => 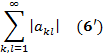

 . По Т** из сходимости двойного ряда (6') => ограниченность его частичных сумм => ограничены частичные суммы двойных рядов
. По Т** из сходимости двойного ряда (6') => ограниченность его частичных сумм => ограничены частичные суммы двойных рядов



 ̶
̶ 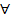 частичная сумма ряда
частичная сумма ряда 
 => послед-сть частичных сумм ряда (11') ограничена=> ряд (11') сходится (по Т***) => (11) сходится абсолютно.
=> послед-сть частичных сумм ряда (11') ограничена=> ряд (11') сходится (по Т***) => (11) сходится абсолютно. } ограничена. Фиксируем
} ограничена. Фиксируем  двойного ряда из модулей (6'). Заведомо найдется номер r настолько большой, что r ̶ я частичная сумма ряда (11) будет содержать все члены, входящие в частичную сумму Sтп ряда (6) =>
двойного ряда из модулей (6'). Заведомо найдется номер r настолько большой, что r ̶ я частичная сумма ряда (11) будет содержать все члены, входящие в частичную сумму Sтп ряда (6) =>  => множество всех частичных сумм двойного ряда (6') ограничено => по Т** ряд (6') сходится.
=> множество всех частичных сумм двойного ряда (6') ограничено => по Т** ряд (6') сходится. ограничена суммой ряда (6') => по Т*** каждый из рядов
ограничена суммой ряда (6') => по Т*** каждый из рядов



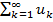 имеет обобщенную сумму U,аряд
имеет обобщенную сумму U,аряд  имеет обобщенную сумму V, то ряд
имеет обобщенную сумму V, то ряд

 } → S, то предел (3) существует и также равен S.
} → S, то предел (3) существует и также равен S.

 => для
=> для 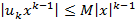 .
.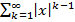 сходится => в силу З** сходится ряд (4).
сходится => в силу З** сходится ряд (4).

 k ̶ й остаток ряда (1):
k ̶ й остаток ряда (1):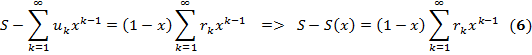
 при k ≥ k 0 =>
при k ≥ k 0 =>
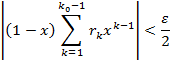
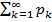 и
и  - 2 ряда с неотрицательными членами. Пусть для всех номеров k справедливо:
- 2 ряда с неотрицательными членами. Пусть для всех номеров k справедливо:  . Тогда из сходимости
. Тогда из сходимости  заменить на:
заменить на:  где с -
где с - 



