
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение и док-во существования двойного интеграла при помощи прямоугольных разбиений. Классы интегрируемых функций. Основные свойства двойного интеграла.Содержание книги
Поиск на нашем сайте Пусть f (х, у)определена всюду на прямоугольнике Разобьем [ a, b ]на п сегментов: На каждом частичном О1. Число
называется интегральной суммой ф-и f (х, у), соответствующей данному разбиению Т прямоугольника R и данному выбору точек О2. Число I называется пределом интегральных сумм (1) при О3. Ф-я f (х, у) называется интегрируемой (по Риману) на прямоугольнике R, если
З. Методом от противного док-тся, что
Составим для данного разбиения Т прямоугольника R верхнюю и нижнюю суммы
У1. Для У2. Для У3. Пусть Т' - измельчение разбиения Т прямоугольника R и S', s ' - верхняя и нижняя суммы Т'. Тогда: У4. Пусть Т' и Т" - У5. Множество { S } верхних сумм данной f (х, у) для всевозможных разбиений прямоугольника R ограничено снизу. Множество нижних сумм { s } ограничено сверху. => У 6. Пусть Т' - измельчение разбиения Т прямоугольника R, полученное из Т добавлением р новых прямых, и пусть S', s' и S, s - верхние и нижние интегральные суммы разбиений Т' и Т. Тогда:
Δ - диаметр разбиения Т, d - диаметр прямоугольника R.
У7. Верхний и нижний интегралы Дарбу Т1. Чтобы ограниченная на прямоугольнике R функция f (х, у) была интегрируема на этом прямоугольнике, необходимо и достаточно, чтобы для Т2. Любая непрерывная в прямоугольнике R функция f (х, у) интегрируема на R. О4. Назовем элементарной фигурой множество точек, представляющих собой объединение конечного числа прямоугольников (со сторонами, параллельными осям Ох и Оу). О5. Ф-я f (х, у) обладает в прямоугольнике R (в произвольной замкнутой области D) I-свойством, если: 1) f (х, у) ограничена в R (в D); 2) для Т3. Если функция f (х, у) обладает в прямоугольнике I-свойством, то она интегрируема на этом прямоугольнике. С-ва двойного интеграла 1°. Аддитивность. Если f (х, у) интегрируема в области D и если область D при помощи кривой Г площади 0 разбивается на две связные и не имеющие общих внутренних точек области D 1 и D 2, то f (х, у) интегрируема в каждой из областей D 1 и D 2, причем
Док-во. Разобьем D 1 и D 2 на конечное число квадрируемых областей, тем самым получим разбиение области D. Пусть D 1 и D 2 . (2) следует из: З. Справедливо и обратное: из интегрируемости f (х, у) в каждой из D 1 и D 2 следует ее интегрируемость в области D и справедливость формулы (2). Док-во. Разбивая D на конечное число квадрируемых частей Di и вводя верхние и нижние суммы функции f (х, у)в D, D 1 и D 2, получим равенства (3), верные с точностью до слагаемых, отвечающих тем областям Di, которые имеют общие внутренние точки с кривой Г. Кривая Г имеет площадь 0, f (х, у)ограничена => общая сумма этих слагаемых → 0 при 2°. Линейное св-во. Пусть f (х, у) и g (х, у) интегрируемы в области D, α и β -
3°. Если f (х, у) и g (х, у) интегрируемы в D, то и произведение этих функций интегрируемо в D. 4°. Если f (х, у) и g (х, у) интегрируемы в D и всюду в D f (х, у) ≤ g (х, у), то
5°. Если f (х, у) интегрируема в области D, то и |f (х, у)| интегрируема в D, причем
(Обратное неверно: из интегрируемости |f (х, у)|в D не вытекает интегрируемость f (х, у)в D) 6°. Если f (х, у) интегрируема в D, а g (х, у) ограничена и совпадает с f (х, у) всюду в D, за исключением множества точек площади 0, то и g (х, у) интегрируема в D. 7°. Теорема о среднем значении. Если f (х, у) и g (х, у) интегрируемы в D, g (х, у) неотрицательна (неположительна) всюду в D,
Если при этом f (х, у) непрерывна в D, а D связна, то в D 8°. Геометрическое св-во.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

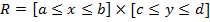 .
.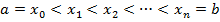 ,[ c, d ]на р сегментов:
,[ c, d ]на р сегментов: 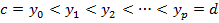 . Этому разбиению сегментов соответствует разбиение T прямоугольника R прямыми, параллельными осям Ох и Оу, на п•р частичных прямоугольников
. Этому разбиению сегментов соответствует разбиение T прямоугольника R прямыми, параллельными осям Ох и Оу, на п•р частичных прямоугольников  .
.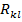 выберем
выберем  точку
точку 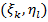 . Положим
. Положим 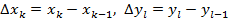 и
и 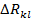 - площадь
- площадь 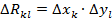 . Длину диагонали
. Длину диагонали 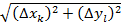 - диаметр
- диаметр  разбиения Т прямоугольника R.
разбиения Т прямоугольника R.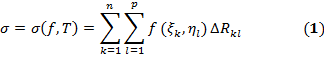
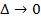 , если для
, если для 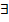 δ > 0: при
δ > 0: при 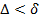 независимо от выбора точек
независимо от выбора точек  на
на 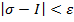 .
.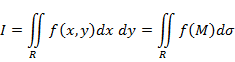
 ограничена на R.
ограничена на R.
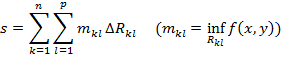
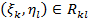 :
: 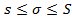 .
. будет удовлетворять
будет удовлетворять  . Точки
. Точки 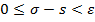 .
.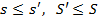 .
.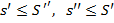 .
. - верхний и нижний интегралы Дарбу от f (х, у)по R.
- верхний и нижний интегралы Дарбу от f (х, у)по R. 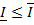 .
.
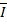 - предел верхних сумм S при Δ→ 0, если для
- предел верхних сумм S при Δ→ 0, если для 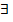 δ > 0:
δ > 0:  при Δ < δ.
при Δ < δ. от f (х, у) по прямоугольнику R являются пределами соответственно верхних и нижних сумм при Δ→ 0.
от f (х, у) по прямоугольнику R являются пределами соответственно верхних и нижних сумм при Δ→ 0.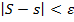 .
.
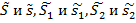 - верхние и нижние суммы f (х, у)в областях D, D 1 и D 2 . Т.к.
- верхние и нижние суммы f (х, у)в областях D, D 1 и D 2 . Т.к. 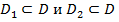 , то
, то 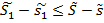 , и
, и  => интегрируемость f (х, у)в
=> интегрируемость f (х, у)в
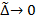 .
.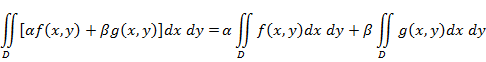
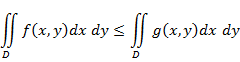

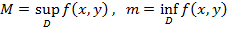
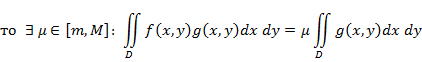
 , что
, что 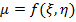 .
.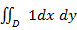 равен площади области D. (см У2 №18)
равен площади области D. (см У2 №18)


