Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Грина. Формула Остроградского-Гаусса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть π - плоскость в 1) граница С области D является замкнутой кусочно гладкой кривой без особых точек; 2) на π можно выбрать такую декартову прямоугольную систему координат, что все прямые, параллельные координатным осям, пересекают D не более чем в 2 точках. Пусть t - единичный вектор касательной к кривой С, согласованный с Т1 (формула Грина). Пусть а - векторное поле, дифф-мое в D, удовлетворяющей условиям 1), 2), и такое, что его производная по
Справа - циркуляция векторного поля Док-во. Все входящие в (1) функции непрерывны => оба интеграла Выберем декартову прямоугольную систему координат Охуz так, чтобы выполнялось условие 2), и Оz направим вдоль
Для плоской области
Для доказательства формулы Грина достаточно доказать 2 равенства:
Пусть прямая, параллельная оси Оу, пересекает С в точках
Аналогично вычисляется интеграл J. З1. Из док-ва => формулу (1) можно записать в виде (1'):
Интегралы слева и справа в (1') инвариантны, т.к. значения подынтегральных выражений равны соответственно
Якобиан преобразования при переходе к новой системе координат по модулю = 1, параметризация с помощью длины дуги не связана с системой координат => интегралы слева и справа в (1') не меняют своего значения и формы. Пусть D - односвязная область в 1) S - кусочно гладкая двусторонняя полная ограниченная замкнутая и без особых точек; 2) прямоугольную декартову систему координат в Пусть n - единичный вектор внешней нормали к S. Т2 (формула Остроградского - Гаусса). Пусть а - векторное поле, дифф-мое в D, удовлетворяющей условиям 1), 2), и такое, что производная по
Cправа - поток векторного поля Док-во Все входящие в (2) функции непрерывны => оба интеграла
Надо док-ть:
Докажем для L, другие ан-но. Пусть D'- проекция D на плоскость Оху. Через граничные точки D' проведем прямые, параллельные Оz. Каждая из них пересекается с S лишь в 1 точке. Множество этих точек разделяет S на 2 части:
Воспользовались тем, что
справедливым, т.к. внешняя нормаль З2. Из док-ва => формулу (2) можно записать:
Док-во ан-но З1. Формула Стокса. Пусть S односвязная (т.е. 1) S - кусочно гладкая двусторонняя полная ограниченная поверхность без особых точек; ее границей является замкнутый кусочно гладкий контур С; 2) декартову систему координат можно выбрать так, чтобы S однозначно проектировалась на Пусть n - единичный вектор нормали к S, t - единичный вектор касательной к C, согласованный с n, т. е. положительное направление обхода кривой С совпадает в точке приложения вектора t с направлением t, и если смотреть с конца Т (формула Стокса). Пусть а - векторное поле, непрерывно дифф-мое в некоторой окрестности поверхности S (т. е. на некотором открытом мн-ве в
Или: Поток вектора Док-во. В силу условий теоремы интегралы в (1) существуют. Формула (1) инвариантна относительно выбора базиса => достаточно доказать при каком-то одном выборе базиса. Выберем прямоугольную декартову систему координат Охуz так, чтобы S однозначно проектировалась на все три координатные плоскости. Пусть
Согласуем выбор системы координат так, чтобы вектор нормали
получим
Достаточно доказать:
S - кусочно гладкая и однозначно проектируется на Оху. Пусть D - ее проекция, Г - проекция С на плоскость Оху =>
и поверхностный интеграл по S = двойному интегралу по D. По формуле Грина*:
З1. Можно выбрать универсальное, не зависящее от Выберем в каждой Разобьем S на конечное число гладких частей З 2. Формула Стокса верна для поверхностей S, допускающих разбиение с помощью кусочно гладких кривых на конечное число односвязных, обладающих свойством 1) поверхностей. Док-во: просуммировать интегралы слева и справа в формулах Стокса для односвязных поверхностей и учесть, что интегралы по кривым, входящим в разбиение, берутся в разных направлениях и поэтому сократятся. З3. Из док-ва => формулу (1) можно записать в виде (1'):
Интегралы слева и справа в (1') инвариантны, т.к. значения подынтегральных выражений равны соответственно
Якобиан преобразования при переходе к новой системе координат по модулю = 1, параметризация с помощью длины дуги не связана с системой координат => интегралы слева и справа в (1') не меняют своего значения и формы. *: π - плоскость в Пусть t - единичный вектор касательной к кривой С, согласованный с Т1 (формула Грина). Пусть а - векторное поле, дифф-мое в D, удовлетворяющей условиям 1), 2), и такое, что его производная по
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 571; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.166.207 (0.007 с.) |

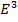 ,
, 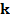 - единичный вектор нормали к π, D - односвязная область на π (т.е.
- единичный вектор нормали к π, D - односвязная область на π (т.е.  кусочно гладкая замкнутая без самопересечений кривая, расположенная в D, ограничивает область, все точки которой также
кусочно гладкая замкнутая без самопересечений кривая, расположенная в D, ограничивает область, все точки которой также  D). Пусть D удовлетворяет условиям:
D). Пусть D удовлетворяет условиям: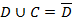 . Тогда справедлива формула
. Тогда справедлива формула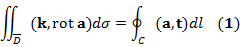
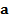 по кривой С, слева - поток векторного поля
по кривой С, слева - поток векторного поля  через D.
через D.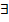 . Интегралы слева и справа в (1) инвариантны относительно выбора прямоугольной системы координат, т.к.
. Интегралы слева и справа в (1) инвариантны относительно выбора прямоугольной системы координат, т.к. 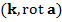 и
и 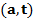 инвариантны, элементы площади
инвариантны, элементы площади 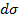 и длины дуги
и длины дуги 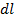 не зависят от выбора декартовой системы координат => достаточно доказать (1) в какой-то одной специально выбранной системе.
не зависят от выбора декартовой системы координат => достаточно доказать (1) в какой-то одной специально выбранной системе.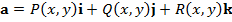 плоское, то
плоское, то  =>
=>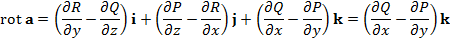
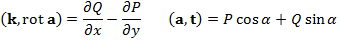
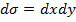 и
и 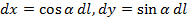 , где l - длина дуги С, выбранная в качестве параметра, возрастание которого согласовано с направлением обхода С =>
, где l - длина дуги С, выбранная в качестве параметра, возрастание которого согласовано с направлением обхода С =>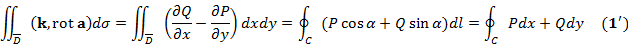
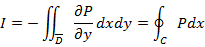
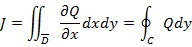
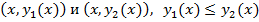 . Пусть
. Пусть 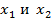 - наименьшая и наибольшая абсциссы точек области
- наименьшая и наибольшая абсциссы точек области  , кривая С 1соединяет
, кривая С 1соединяет 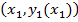 с
с 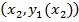 , а кривая С 2 -
, а кривая С 2 - 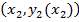 с
с  и
и 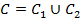 ,
,  ориентированы согласованно с C => по формуле сведения двойного интеграла к повторному:
ориентированы согласованно с C => по формуле сведения двойного интеграла к повторному:


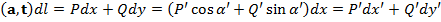

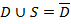 . Тогда
. Тогда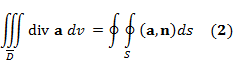
 => учитывая
=> учитывая 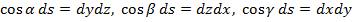 :
:
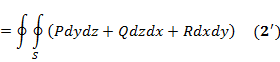

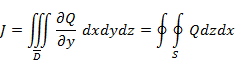
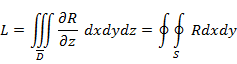
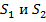 . Если провести прямую из внутренней точки D', параллельную Оz, то она пересечет S в 2 точках:
. Если провести прямую из внутренней точки D', параллельную Оz, то она пересечет S в 2 точках: 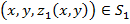 и
и  .
.  и
и  кусочно и непрерывно дифф-мые функции в D'. По формуле сведения тройного интеграла к повторному интегралу:
кусочно и непрерывно дифф-мые функции в D'. По формуле сведения тройного интеграла к повторному интегралу:

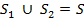 , и соотношением
, и соотношением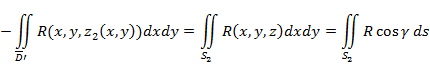
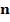 к
к  образует тупой угол с Оz (=>
образует тупой угол с Оz (=> 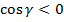 ).
).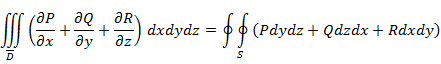


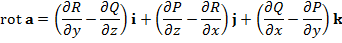




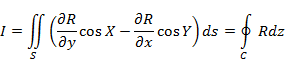
 , которая задает уравнение поверхности S. При этом
, которая задает уравнение поверхности S. При этом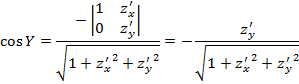
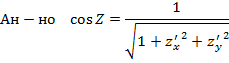
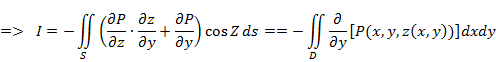
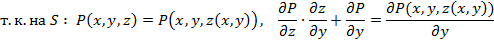
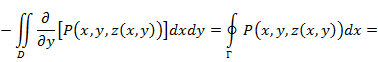
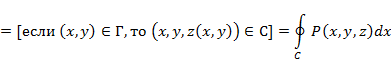
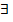 δ > 0 такое, что для
δ > 0 такое, что для 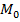 - фиксированная точка S. Проведем касательную плоскость через
- фиксированная точка S. Проведем касательную плоскость через 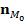 - вектор единичной нормали поверхности в
- вектор единичной нормали поверхности в 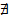 => для каждого
=> для каждого 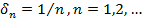 можно указать часть
можно указать часть 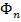 поверхности S, размеры которой <
поверхности S, размеры которой < 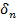 и которая не проектируется однозначно на все координатные плоскости
и которая не проектируется однозначно на все координатные плоскости 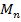 , из полученной послед-сти выберем послед-сть, сходящуюся к некоторой М
, из полученной послед-сти выберем послед-сть, сходящуюся к некоторой М 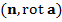 , а справа - интеграл по границе С от
, а справа - интеграл по границе С от