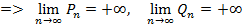Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие числового ряда. Критерий Коши.Содержание книги
Поиск на нашем сайте
Арифметические операции над сходящимися числовыми рядами. Теорема Мертенса. О. Ряд О1. Ряд Т1. Если 2 ряда Док ̶ во. Пусть
по Т (Сумма (разность) сходящихся послед-стей является сходящейся послед-стью, предел которой равен сумме (разности) пределов этих послед-стей). Т2. Если 2 ряда Док ̶ во. Пусть w 1, w 2, w 3, … - произведения вида
Здесь в правой части стоит произведение m - х частичных сумм рядов
Произведение рядов
Т3 (теорема Мертенса). Ряд, полученный перемножением двух рядов указанным специальным способом, сходится к произведению сумм перемножаемых рядов в случае, когда один из перемножаемых рядов сходится абсолютно, а другой ̶ сходится хотя бы условно. Док-во. Пусть
Положим Достаточно доказать, что Элементарно проверяется, что Из сходимости
где Т.к.
И
Представив β n в виде и выбрав по т номер п 1настолько большим, что при k > n 1 ̶ m (это можно сделать в силу бесконечной малости { α n }), с помощью неравенств:
(при k > n 1 ̶ m) получим, что при п ≥ п 1в выражении для β n каждая |[ ]| < ε/2 => | β n | < ε при п ≥ п 1. Т.к. ε > 0 произвольно => {β n } - бесконечно малая послед-сть.
Формула Стокса. Пусть S односвязная (т.е. 1) S - кусочно гладкая двусторонняя полная ограниченная поверхность без особых точек; ее границей является замкнутый кусочно гладкий контур С; 2) декартову систему координат можно выбрать так, чтобы S однозначно проектировалась на Пусть n - единичный вектор нормали к S, t - единичный вектор касательной к C, согласованный с n, т. е. положительное направление обхода кривой С совпадает в точке приложения вектора t с направлением t, и если смотреть с конца Т (формула Стокса). Пусть а - векторное поле, непрерывно дифф-мое в некоторой окрестности поверхности S (т. е. на некотором открытом мн-ве в
Или: Поток вектора Док-во. В силу условий теоремы интегралы в (1) существуют. Формула (1) инвариантна относительно выбора базиса => достаточно доказать при каком-то одном выборе базиса. Выберем прямоугольную декартову систему координат Охуz так, чтобы S однозначно проектировалась на все три координатные плоскости. Пусть
Согласуем выбор системы координат так, чтобы вектор нормали
получим
Достаточно доказать:
S - кусочно гладкая и однозначно проектируется на Оху. Пусть D - ее проекция, Г - проекция С на плоскость Оху =>
и поверхностный интеграл по S = двойному интегралу по D. По формуле Грина*:
З1. Можно выбрать универсальное, не зависящее от Выберем в каждой Разобьем S на конечное число гладких частей З 2. Формула Стокса верна для поверхностей S, допускающих разбиение с помощью кусочно гладких кривых на конечное число односвязных, обладающих свойством 1) поверхностей. Док-во: просуммировать интегралы слева и справа в формулах Стокса для односвязных поверхностей и учесть, что интегралы по кривым, входящим в разбиение, берутся в разных направлениях и поэтому сократятся. З3. Из док-ва => формулу (1) можно записать в виде (1'):
Интегралы слева и справа в (1') инвариантны, т.к. значения подынтегральных выражений равны соответственно
Якобиан преобразования при переходе к новой системе координат по модулю = 1, параметризация с помощью длины дуги не связана с системой координат => интегралы слева и справа в (1') не меняют своего значения и формы. *: π - плоскость в Пусть t - единичный вектор касательной к кривой С, согласованный с Т1 (формула Грина). Пусть а - векторное поле, дифф-мое в D, удовлетворяющей условиям 1), 2), и такое, что его производная по
Понятие числового ряда. Критерий Коши. Из элементов
Сумма (1) ̶ числовой ряд, иk ̶ члены ряда (1). Сумма первых п членов ̶ п ̶ я частичная сумма а:
О. Ряд (1) называется сходящимся, если сходится послед-сть { Sп } частичных сумм (2) этого ряда. Предел S послед-сти { Sп } - сумма ряда (1): Если для ряда (1) З1. Изучение числовых рядов - новая форм изучения числовых последовательностей: 1) каждому ряду (1) однозначно соответствует послед-сть { Sп }его частичных сумм, 2) З2. Из определения его сходимости => cв-ва произвольного ряда: I. Отбрасывание конечного числа членов ряда (или добавление конечного числа членов) не влияет на сходимость или расходимость этого ряда. (Т.к. в после отбрасывания (или добавления) конечного числа членов все частичные суммы ряда, начиная с некоторого n, изменятся на одну и ту же const.) II. Если с = const ≠ 0,
Критерий Коши для послед-сти: Чтобы послед-сть { Sп } была сходящейся, необходимо и достаточно, чтобы для
Т1 (критерий Коши для ряда). Чтобы ряд
Док-во. Сл1. Если ряд Док-во. Из (3) и из Т (Если все элементы сходящейся послед-сти { хп }, по крайней мере начиная с некоторого номера, удовлетворяют неравенству хп ≥ b [ хп ≤ b ], то и предел х этой послед-сти удовлетворяет неравенству х ≥ b [ х ≤ b ]) => для Сл2 (необходимое условие сходимости ряда). Для сходимости ряда Док-во. Пусть дано | иn+ 1| < ε (при п ≥ N) =>если положить N 0 = N+ 1, то при п ≥ N 0: | иn | < ε • Основное св-во ряда с неотрицательными членами: послед-сть частичных сумм такого ряда является неубывающей. Т 2. Чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы послед-сть частичных сумм этого ряда была ограничена. Необходимость из Т: Всякая сходящаяся последовательность является ограниченной. Достаточность: послед-сть частичных сумм не убывает => для ее сходимости достаточно, чтобы она была ограничена (по Т: Если неубывающая послед-сть ограничена сверху, то она сходится).
2. Признаки сходимости рядов с неотрицательными членами (признаки сравнения. Даламбера, Коши, Коши ̶ Маклорена). О. Ряд Основное св-во ряда с неотрицат. членами: послед-сть частичных сумм ряда - неубывающая. Т1. Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы послед-сть частичных сумм этого ряда была ограничена. Необх-сть из Т: Всякая сходящаяся послед-сть является ограниченной. Дост-сть: послед-сть частичных сумм не убывает => для ее сходимости достаточно, чтобы она была ограничена (по Т: Если неубывающая послед-сть ограничена сверху, то она сходится). Т2. Пусть Тогда из сходимости Док ̶ во. Пусть 1)из ограниченности послед-сти { Sn '} => ограниченность послед-сти { Sn }; 2) из неограниченности послед-сти { Sn } => неограниченность послед-сти { Sn '}. И применяем Т1. • З. 1) В условии Т2 можно требовать, чтобы (1) было выполнено а лишь начиная с некоторого номера k, т.к. отбрасывание конечного числа членов не влияет на сходимость ряда. 2) Т2 будет справедливой, если (1) заменить: где с - Сл. Если
то из сходимости Док ̶ во. Т. к. то для некоторого ε > 0
=> при k ≥ N: Т3. Пусть
Тогда из сходимости Док ̶ во. Запишем (3) для k = 1, 2, …, п - 1, где п -
…
Перемножая почленно все написанные неравенства, получим
Признаки Даламбера и Коши основаны на сравнении ряда со сходящимся (4) или расходящимся (5)
Т4 (пр-к Даламбера). I. Если для всех номеров k, по крайней мере начиная с некоторого номера:
то II. (Пр-к Даламбера в предельной форме). Если
то Док ̶ во. I) Положим
Т.к. ряд II) Если L < 1, то
L + ε =1 ̶ ε = q в TI. Ряд сходится. Если же L > 1, то
Ряд З. 1) в Т4(I)
расходится, но здесь 2) При L = 1 в Т4(II)нельзя сказать ничего определенного о сходимости ряда: для гармонического ряда L= 1, причем он расходится. Но для Т5 (признак Коши). I. Если для всех номеров k, по крайней мере начиная с некоторого номера:
то II. (признак Коши в предельной форме). Если
то Док ̶ во. I) Положим Т.к. II) Дословно повторить док-во Т4(II), заменив З. Аналогичны замечаниям к Т4. Пр-к Коши более сильный, чем пр-к Даламбера: когда действует пр-к Даламбера, действует и пр-к Коши, но Утв. Из существования равного L, предела
=> существование равного тому же L предела Л1. Если послед-сть { ап } → l, то к тому же l сходится и послед-сть σп = (а 1+ a 2 + … +ап) / п средних арифметических чисел а 1, а 2 ,...,ап. Док- во. { ап } → l => для
получим, что Модуль дроби в {} ≤ Л2. Если { ап } → L (все ап > 0), то к L сходится и послед-сть Док ̶ во. Для L > 0 силу непрерывности логарифмической функции
=> т.к. показательная функция непрерывна, то
(Эти рассуждения справедливы и при L = 0, если считать ln L = ̶ ∞.) Док-во утв-я. Применяя Л2 к числам а 1 = p 1, а 2 = р 2 /р 1, …, ап = рп / рп ̶ 1и т.к.
установим существование равного тому же L предела Т6. (признак Коши - Маклорена). Пусть f (х) неотрицательна и не возрастает всюду на полупрямой х ≥ m, где т ̶
сходится ó
Док ̶ во. Пусть k ̶ f (x) ограниченна (0-м) и монотонна => интегрируема на [ k ̶ 1, k ]. Из (15) и из свойства интеграла
(16) установлены для
Из (14) => послед-сть { ап }- неубывающая => для ее сходимости необходима и достаточна ее ограниченность. Для сходимости (13) по Т1 необходима и достаточна ограниченность послед-сти { Sn }. Из (18) => { Sn } ограничена ó ограничена { ап } ó { ап } сходится.
3. Теоремы Коши иРимана о перестановке членов в числовых рядах. О1. Ряд Т1. Из сходимости ряда (2) вытекает сходимость ряда (1). Док-во. Используем критерий Коши для ряда (Чтобы ряд
Фиксируем
Так как модуль суммы нескольких слагаемых не превосходит суммы их модулей, то
Сопоставляя эти 2 неравенства, получим неравенства (3). О2. Ряд (1) называется условно сходящимся, если этот ряд сходится, в то время как соответствующий ряд из модулей (2) расходится. Пример абсолютно сходящегося ряда:
Пример условно сходящегося ряда:
Т2. (теорема Римана). Если ряд сходится условно, то, каково бы ни было наперед взятое число L, можно так переставить члены этого ряда, чтобы преобразованный ряд сходился к числу L. Док ̶ во. Пусть (1) ̶ Докажем, что ряды
Но т.к. (1) не сходится абсолютно, то
т. е. оба ряда Р и Q расходятся=> даже после удаления любого конечного числа первых членов этих рядов, мы можем взять из оставшихся членов рядов Р и Q столь большое число членов, что их сумма превзойдет любое наперед взятое число. Выберем из (1) ровно столько положительных р 1, p 2, …, рk1, чтобы р 1 + p 2 + … + рk1 > L. Добавим ровно столько отрицательных ̶ q1, ̶ q 2 ,…, ̶ qk2, чтобы р 1 + p 2 + … + рk1 ̶ q1 ̶ q 2 ̶ … ̶ qk2 < L. Затем снова добавим рk 1+1, p k 1+2, …, рk2, чтобы р 1 + p 2 + … + рk1 ̶ q1 ̶ q 2 ̶ … ̶ qk2 + рk 1+1 + p k 1+2 + …+ рk2 > L. Продолжая, получим бесконечный ряд, в состав которого войдут все члены исходного ряда (1), т.к. каждый раз придется добавлять хотя бы 1 положительный или отрицательный член исходног
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.211.55 (0.012 с.) |

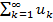 называется сходящимся, если сходится послед-сть { Sп } частичных сумм (2) этого ряда. Предел S послед-сти { Sп } - сумма ряда (1):
называется сходящимся, если сходится послед-сть { Sп } частичных сумм (2) этого ряда. Предел S послед-сти { Sп } - сумма ряда (1): 

 сходятся и имеют суммы соот-но U и V, то и ряд
сходятся и имеют суммы соот-но U и V, то и ряд  сходится и имеет сумму
сходится и имеет сумму  .
.

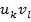 (k =1, 2,...; l = 1, 2,...), занумерованных в
(k =1, 2,...; l = 1, 2,...), занумерованных в  порядке, также сходится абсолютно и его сумма равна UV.
порядке, также сходится абсолютно и его сумма равна UV.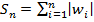 . Сумма Sn состоит из членов вида
. Сумма Sn состоит из членов вида  . Пусть т - наибольший среди индексов k и l членов, входящих в Sn. Тогда
. Пусть т - наибольший среди индексов k и l членов, входящих в Sn. Тогда
 и
и  => из сходимости этих рядов с неотрицательными членами все их частичные суммы (=> и их произведение) ограничены => ограничена { Sn } => ряд
=> из сходимости этих рядов с неотрицательными членами все их частичные суммы (=> и их произведение) ограничены => ограничена { Sn } => ряд 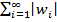 сходится => ряд
сходится => ряд  сходится абсолютно => его сумма S не зависит от порядка суммирования по теореме Коши (Если данный ряд сходится абсолютно, то любой ряд, полученный из данного посредством некоторой перестановки членов, также сходится абсолютно и имеет ту же сумму, что и данный ряд.).
сходится абсолютно => его сумма S не зависит от порядка суммирования по теореме Коши (Если данный ряд сходится абсолютно, то любой ряд, полученный из данного посредством некоторой перестановки членов, также сходится абсолютно и имеет ту же сумму, что и данный ряд.).  , т.к. { Wт } → UV, где Wт = (u 1+…+ um) (v 1+…+ vm). •
, т.к. { Wт } → UV, где Wт = (u 1+…+ um) (v 1+…+ vm). •

 ,
, 


 - бесконечно малая => ограниченная послед-сть =>
- бесконечно малая => ограниченная послед-сть => 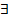 М:
М:  для всех п. Заметим, что
для всех п. Заметим, что

 , то достаточно доказать, что {β n } - бесконечно малая послед-сть. Т.к.
, то достаточно доказать, что {β n } - бесконечно малая послед-сть. Т.к. 



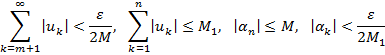
 S) поверхность в
S) поверхность в 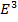 , удовлетворяющая условиям:
, удовлетворяющая условиям: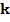 , то контур С ориентирован положительно (его обход против часовой стрелки).
, то контур С ориентирован положительно (его обход против часовой стрелки).
 через поверхность S равен циркуляции вектора а по замкнутому контуру С.
через поверхность S равен циркуляции вектора а по замкнутому контуру С.
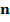 образовывал острые углы с координатными осями. Учитывая выражение для
образовывал острые углы с координатными осями. Учитывая выражение для 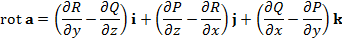




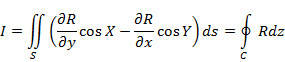
 , которая задает уравнение поверхности S. При этом
, которая задает уравнение поверхности S. При этом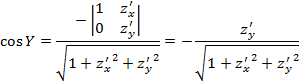
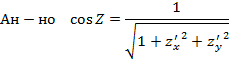
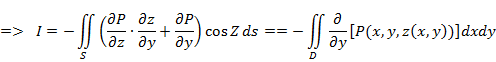
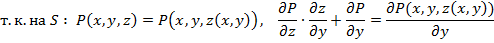
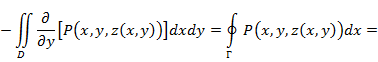
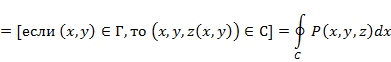
 δ > 0 такое, что для
δ > 0 такое, что для 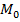 - фиксированная точка S. Проведем касательную плоскость через
- фиксированная точка S. Проведем касательную плоскость через 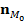 - вектор единичной нормали поверхности в
- вектор единичной нормали поверхности в 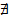 => для каждого
=> для каждого 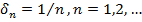 можно указать часть
можно указать часть 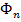 поверхности S, размеры которой <
поверхности S, размеры которой < 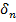 и которая не проектируется однозначно на все координатные плоскости
и которая не проектируется однозначно на все координатные плоскости 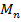 , из полученной послед-сти выберем послед-сть, сходящуюся к некоторой М
, из полученной послед-сти выберем послед-сть, сходящуюся к некоторой М 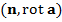 , а справа - интеграл по границе С от
, а справа - интеграл по границе С от 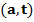 , т. е. формулу Стокса для общего случая => формулы Стокса справедлива для поверхностей, удовлетворяющих условию 1) и не удовлетворяющих, вообще говоря, условию 2).
, т. е. формулу Стокса для общего случая => формулы Стокса справедлива для поверхностей, удовлетворяющих условию 1) и не удовлетворяющих, вообще говоря, условию 2).
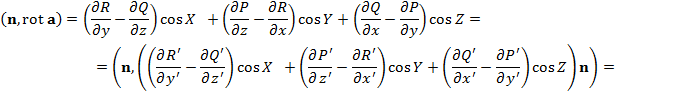
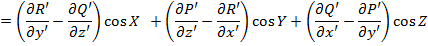
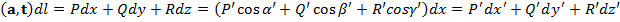
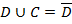 . Тогда справедлива формула
. Тогда справедлива формула
 формально образуем бесконечную сумму:
формально образуем бесконечную сумму:

 .
. , то ряд
, то ряд 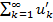 сходится ó сходится ряд
сходится ó сходится ряд  и
и  и учитывая
и учитывая  , где с ≠ 0 =>
, где с ≠ 0 =>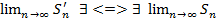 )
) :
:

 и применить критерий Коши для послед-сти.
и применить критерий Коши для послед-сти. является бесконечно малой.
является бесконечно малой. при п ≥ N.
при п ≥ N. ).
).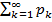 и
и  - 2 ряда с неотрицательными членами и для всех номеров k справедливо неравенство
- 2 ряда с неотрицательными членами и для всех номеров k справедливо неравенство 
 =>
=>



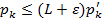 =>это нерав-во совпадает с (2) при
=>это нерав-во совпадает с (2) при  . И применить З 2.
. И применить З 2.




 - const > 0, не зависящая от п => применим З2. •
- const > 0, не зависящая от п => применим З2. •



 сходится при L < 1 и расходится при L > 1.
сходится при L < 1 и расходится при L > 1. . Тогда
. Тогда 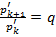 , где q < 1 (
, где q < 1 ( ), и перепишем (6):
), и перепишем (6):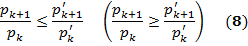


 нельзя заменить на
нельзя заменить на  : гармонический ряд
: гармонический ряд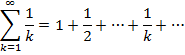
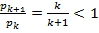 (для всех k).
(для всех k). тоже L= 1,но он сходится.
тоже L= 1,но он сходится.

 => из (10):
=> из (10): 
 на
на  .
.
 при всех п ≥ N 1.
при всех п ≥ N 1.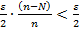 . Т.к. N фиксирован, то модуль дроби в [ ] ≤ ε /2 при всех п ≥ N 1, где N 1 ̶ достаточно большое число =>
. Т.к. N фиксирован, то модуль дроби в [ ] ≤ ε /2 при всех п ≥ N 1, где N 1 ̶ достаточно большое число =>  средних геометрических чисел а 1, а 2 ,...,ап.
средних геометрических чисел а 1, а 2 ,...,ап.












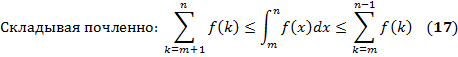
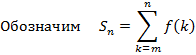
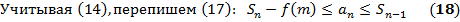
 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 
 N: для
N: для 



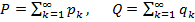 с положительными членами - расходящиеся. Обозначим
с положительными членами - расходящиеся. Обозначим  , Рп - сумму всех положительных членов, входящих в Sп, Qп - сумму модулей всех отрицательных членов, входящих в Sп => Sп = Рп ̶ Qп. Т.к. по условию ряд (1) сходится к некоторому числу S, то
, Рп - сумму всех положительных членов, входящих в Sп, Qп - сумму модулей всех отрицательных членов, входящих в Sп => Sп = Рп ̶ Qп. Т.к. по условию ряд (1) сходится к некоторому числу S, то