
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение двойного интеграла при помощи произвольных разбиений области. Эквивалентность двух определений.Содержание книги
Поиск на нашем сайте
Плоская фигура - часть плоскости, ограниченная простой замкнутой кривой. Плоская фигура называется квадрируемой, если верхняя и нижняя площади этой фигуры равны между собой (Верхняя площадь - точная нижняя грань площадей всех многоугольников, содержащих фигуру, нижняя площадь - точная верхняя грань площадей всех многоугольников, содержащихся в фигуре.). Это число называется площадью фигуры. Г называется кривой площади 0, если для У1. Пусть кривая Г имеет площадь 0 и плоскость покрыта квадратной сеткой с шагом h. Тогда для Док-во. Для каждого ε > 0 можно фиксировать некоторую элементарную фигуру Q, содержащую внутри себя Г и имеющую площадь, меньшую ε/4. При достаточно малом h все квадраты, имеющие общие с Г точки, содержатся в элементарной фигуре, получающейся заменой каждого прямоугольника прямоугольником со вдвое большими сторонами и с тем же центром.• Пусть D - замкнутая ограниченная область, граница Г которой имеет площадь 0, f (х, у) -
О1. Ф-я f (х, у) интегрируема в D, если ф-я F (х, у) интегрируема в прямоугольнике R. Число
назовем двойным интегралом от f (х, у) по области D и обозначим:
У2. Интеграл Док-во. Подвергая прямоугольник R все более мелким разбиениям, получим, что верхние интегральные суммы этих разбиений будут равны площадям элементарных фигур, содержащих D, а нижние суммы - площадям элементарных фигур, содержащихся в D. Интегрируемость f (х, у)=1в D следует из Т*. Т1. Если f (х, у) обладает в области D I-свойством, то она интегрируема в этой области. Док-во. Функция F (х, у), определенная (1), обладает I -свойством в прямоугольнике R, т.к. F (х, у)ограничена в R ивсе ее точки и линии разрыва либо совпадают с соответствующими разрывами f (х, у),либо лежат на границе Г области D. Но граница Г имеет площадь 0=> Т1 следует из Т*. Сл1. Если f (х, у) ограничена в D и имеет в D разрывы лишь на конечном числе спрямляемых линий, то f (х, у) интегрируема в D.
Сл2. Если f (х, у) обладает в D I-свойством, а g (х, у) ограничена и совпадает с f (х, у) всюду в D, за исключением множества точек площади 0, то g (х, у) интегрируема в области D, причем
Пусть D - замкнутая ограниченная область с границей Г площади 0. Разобьем область D при помощи конечного числа произвольных кривых площади 0 на конечное число r замкнутых частичных областей D 1, D 2, ..., Dr. Каждая О2. Число
называется интегральной суммой ф-и f (х, у), соответствующей данному разбиению D на частичные области
О3. Число I называется пределом интегральных сумм (2) при О4 (общее определение интегрируемости). Ф-я f (х, у) называется интегрируемой (по Риману) в области D если Т2. Общее определение интегрируемости эквивалентно определению 1. Док-во. 1) Пусть f (х, у)интегрируема в D согласно O4 и ее двойной интеграл согласно O4 равен I. Заключим D в прямоугольник R, разобьем его на частичные прямоугольники и введем на R ф-ю F (х, у)по правилу (1). Рассмотрим для этого разбиения интегральную сумму (2) 2) Пусть f (х, у)интегрируема в D согласно О1 и I - двойной интеграл от f (х, у)по D согласно О1. Докажем, что для f (х, у)
Т.к. для Фиксируем
Заключим все отрезки прямых, производящих разбиение Т, и границу Г области D строго внутрь элементарной фигуры Q, площадь которой меньше числа
Докажем 1-е неравенство (4) (2-е ан-но). Удалим из
где штрих обозначает, что сумма распространена лишь на Заменим в правой части (5) точные грани
и
Для прямоугольников
для прямоугольников
=> и из (6):
=> 1-е неравенство (4) =>
Из (3) => каждая из s и S отклоняется от I меньше чем на ε /2 => каждая из *: О. Ф-я f (х, у) обладает в прямоугольнике R (в произвольной замкнутой области D) I-свойством, если: 1) f (х, у) ограничена в R (в D); 2) для Т. Если f (х, у) обладает в прямоугольнике I-свойством, то она интегрируема на этом прямоугольнике. **: Чтобы ограниченная на прямоугольнике R ф-я f (х, у) была интегрируема на R, необходимо и достаточно, чтобы для О0. Число
назовем интегральной суммой ф-и f (х, у), соответствующей данному разбиению Т прямоугольника R и данному выбору промежуточных точек О0’. Число I называется пределом интегральных сумм (8) при
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.46.13 (0.009 с.) |

 ε > 0
ε > 0 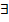 многоугольник (элементарная фигура), содержащий все точки Г и имеющий площадь, меньшую ε.
многоугольник (элементарная фигура), содержащий все точки Г и имеющий площадь, меньшую ε.


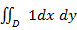 равен площади области D.
равен площади области D.
 имеет границу площади 0 => квадрируема. Пусть
имеет границу площади 0 => квадрируема. Пусть  - площадь области
- площадь области 

 в
в 
 - расстояние между
- расстояние между  . Диаметр разбиения D - число
. Диаметр разбиения D - число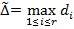
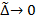 , если для
, если для  < δ независимо от выбора точек
< δ независимо от выбора точек  .
. этой функции при
этой функции при  ф-и F (х, у). Эти суммы могут отличаться лишь слагаемыми, соответствующими частичным прямоугольникам разбиения, имеющим общие точки с границей Г области D. Поскольку Г имеет площадь 0, а f (х, у)ограничена, то f (х, у)интегрируема и согласно О1. По О1 она имеет тот же самый двойной интеграл I.
ф-и F (х, у). Эти суммы могут отличаться лишь слагаемыми, соответствующими частичным прямоугольникам разбиения, имеющим общие точки с границей Г области D. Поскольку Г имеет площадь 0, а f (х, у)ограничена, то f (х, у)интегрируема и согласно О1. По О1 она имеет тот же самый двойной интеграл I.
 , то надо доказать, что обе суммы
, то надо доказать, что обе суммы  стремятся к I при
стремятся к I при  :
:  .
. R)на частичные прямоугольники Rk такое, что для соответствующей функции F (х, у)
R)на частичные прямоугольники Rk такое, что для соответствующей функции F (х, у)
 =>
=>  :
:
 все слагаемые
все слагаемые 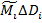 , соответствующие областям
, соответствующие областям  (т.к.
(т.к.  ) => общая сумма площадей таких областей меньше числа
) => общая сумма площадей таких областей меньше числа 
 в
в  , точной верхней гранью
, точной верхней гранью  в прямоугольнике
в прямоугольнике 
 - площадь области
- площадь области  =>
=>
 области
области  , поэтому для них
, поэтому для них

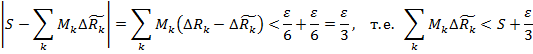


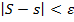 .
.
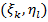 на частичных прямоугольниках разбиения Т.
на частичных прямоугольниках разбиения Т.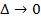 , если для
, если для 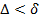 независимо от выбора промежуточных точек
независимо от выбора промежуточных точек  на
на 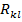 выполняется
выполняется 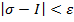 .
.


