Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дивергенция, ротор и производная по направлению векторного поля. Повторные операции теории поля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В области D задано скалярное поле, если каждой точке М В области D задано векторное поле, если каждой точке М Пусть задано скалярное поле О1. Скалярное поле
где Условие дифференцируемости скалярного поля
где
где О1*. Скалярное поле (1) можно переписать:
(2) приводит к векторному полю градиента дифференцируемого в области D скалярного поля
Производная по направлению задает некоторое новое скалярное поле в области D. Пусть в области D пр-ва О2. Векторное поле где А - некоторый линейный оператор в
Утв. Если векторное поле дифференцируемо, то представление (4) единственно. Док-во. Если есть 2 представления вида (4):
то Разделим на
где Если 2 ЛО А и В совпадают на единичной сфере, то они равны на Векторное поле дифференцируемо в области D, если оно дифференцируемо в каждой точке D. Пусть М О3. Производной векторного поля
Утв. Пусть векторное поле
Док-во. Пусть
Переходя к пределу при Рассмотрим (4):
По формулам* вычисляем элементы матрицы
Пусть О4. Дивергенцией векторного поля
О5. Ротором векторного поля
Т.к. Выберем ортонормированный базис i, j, k и свяжем с ним декартову систему координат Охуz. Пусть в i, j, k координаты поля
Т.к.
Вычислим производную поля
Пусть в D заданы скалярное поле Пусть i, j, k - фиксир. ортонормир. базис, с которым связана декартова система координат Oхуz. Утв. Имеют место следующие 5 соотношений:
Док-во. Схема: последовательно применять операторы к скалярному или векторному полю. 1)
Δ («дельта») - оператор Лапласа:
Подставляя вместо b его выражение, получим правую часть 3-го соотношения. З. grad, div, rot инвариантны => инвариантны *:
**: ***:
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 960; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 D сопоставлено по некоторому закону число
D сопоставлено по некоторому закону число  => понятия скалярного поля и скалярной функции, определенной в D, совпадают.
=> понятия скалярного поля и скалярной функции, определенной в D, совпадают. => понятия векторного поля и векторной функции, определенной в D, совпадают.
=> понятия векторного поля и векторной функции, определенной в D, совпадают. в области D из
в области D из 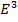 .
.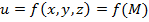 называется дифференцируемым в
называется дифференцируемым в 
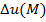 в M можно представить в виде
в M можно представить в виде
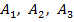 - некоторые не зависящие от
- некоторые не зависящие от  числа,
числа,  - бесконечно малые при
- бесконечно малые при  функции, равные 0 при
функции, равные 0 при 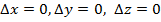 .
.
 , это представление единственно. В более компактном виде:
, это представление единственно. В более компактном виде:
 - скалярное произведение векторов
- скалярное произведение векторов 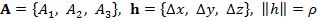 .
. дифференцируемо в М, если в этой точке для полного приращения справедливо соотношение (1). Скалярное поле
дифференцируемо в М, если в этой точке для полного приращения справедливо соотношение (1). Скалярное поле 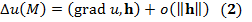
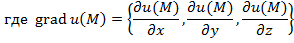
 :
:
 ,оно каждой точке
,оно каждой точке  представляется в виде
представляется в виде 

 - вектор, длина которого после деления на
- вектор, длина которого после деления на  стремится к 0 при |
стремится к 0 при | 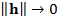 .
.



 - вектор единичной длины. Справа стоит бесконечно малый вектор (его длина → 0 при |
- вектор единичной длины. Справа стоит бесконечно малый вектор (его длина → 0 при |  единичного вектора
единичного вектора 
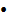
 .
.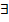 ):
):
 ). Тогда производная
). Тогда производная 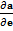 поля в этой точке М по любому направлению
поля в этой точке М по любому направлению 
 => из (4)
=> из (4)  . Т.к.
. Т.к.  , то
, то
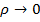 , получаем (5).
, получаем (5).  из
из  . Из (5) =>
. Из (5) =>
 оператора А:
оператора А: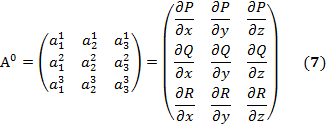
 при
при 

 и
и  определены в каждой М
определены в каждой М 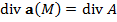 , то по формулам** и (7)
, то по формулам** и (7)

 , то по формулам*** и (7):
, то по формулам*** и (7):









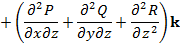



 =
= 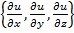 => из (9):
=> из (9):

 .
.

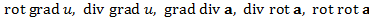 => в
=> в