
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные элементарных функций (вывод одной из них)⇐ ПредыдущаяСтр 11 из 11
Выведем формулу нахождения производной показательной функции y=ax. Придавая аргументу х приращение ∆х, находим для приращения функции ∆у следующее значение: ∆у=ах+∆х - ах = ах(а∆х - 1). Делим на ∆х: 6. Правила дифференцирования Операция отыскания производной от данной функции называется дифференцированием этой функции.Установим ряд правил, которые избавят нас от необходимости вычислять производную исходя непосредственно из ее определения. Правило дифференцирования обратной функции
7. производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления. Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению. Рассмотрим функцию
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате. Производную по направлению можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
Где 8. Дифференциальные уравнения вида (3), которое может быть представлено в виде называются дифференциальными уравнениями первого порядка с разделяющимися переменными. Метод интегрирования таких уравнений состоит в следующем. Если в уравнении (4) производную
Если функции полученные дифференциальные уравнения (6) и (7) называются дифференциальными уравнениями первого порядка с разделенными переменными.
9. Теорема (сложения вероятностей). Вероятность суммы двух случайных событий равна сумме вероятностей этих событий минус вероятность их пересечения:
Доказательство. Очевидно:
Тогда Поскольку события АВ и
События
Итак,
Следствие 1: Верно следующее обобщение формулы для трех слагаемых:
Следствие 2: Верно следующее обобщение формулы для слагаемых n:
10. Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило. т.е. Р(АВ)= Р(А)РА(В). Доказательство: Пусть в результате опыта возможны N исходов, из них М благоприятствуют появлению события А, их этихМ- К исходов благоприятствуют событию В. Одновременному появлению событий А и В благоприятствуют L исходов из К.. По классической формуле имеем: Р(АВ)=L/N. Умножим и разделим на М: Первая дробь- вероятность наступления события А, вторая- вероятность события В, при условии, что А уже произошло, т.е. условная вероятность события В, что и требовалось доказать. Теорема2: Вероятность произведения двух независимых событий А и В равна произведению их вероятностей Р(АВ)=Р(А)Р(В). Доказательство: Т.к. события независимые, то верно равенство РА(В)=Р(В), тогда получим Р(АВ)=Р(А)Р(В). 11. Формула Бернулли — формула в теории вероятности, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу. Теорема: Если Вероятность ρ наступления события Α в каждом испытании постоянна, то вероятность Pk,n того, что событие A наступит k раз в n независимых испытаниях, равна: где q = 1-p Доказательство: Так как в результате n независимых испытаний, проведенных в одинаковых условиях, событие A наступает с вероятностью, следовательно противоположное ему событие с вероятностью. Обозначим Ai — наступление события A в испытании с номером i. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате n опытов событие A наступает k раз, тогда остальные n − k − раз это событие не наступает. Событие A может появиться k раз в n испытаниях в различных комбинациях, число которых равно количеству сочетаний из n элементов по k. Это количество сочетаний находится по формуле: При этом вероятность каждой комбинации равна произведению вероятностей: Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли: где q = 1-p
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.202 (0.023 с.) |
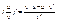 x'y=1/y’x
x'y=1/y’x
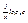 , (lnx)’=1/x
2. (xn)’=nxn-1
3. (sinx)’=cosx, (cosx)’= - sinx
4. (tgx)’=sec2x, (ctgx)’= -
, (lnx)’=1/x
2. (xn)’=nxn-1
3. (sinx)’=cosx, (cosx)’= - sinx
4. (tgx)’=sec2x, (ctgx)’= - 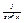 = cosec2x
5. (arcsin)’=
= cosec2x
5. (arcsin)’= 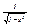 , (arcos)’=
, (arcos)’= 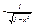 6. (arctgx)’=
6. (arctgx)’= 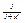 , (arcctg)’= -
, (arcctg)’= -  . Переходим к пределу при ∆х"0:
. Переходим к пределу при ∆х"0: 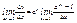 , но
, но 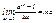 . Поэтому у'х=ахlna. Итак, (ax)’=axlna, в частности (ex)’=ex (так как lne=1).
. Поэтому у'х=ахlna. Итак, (ax)’=axlna, в частности (ex)’=ex (так как lne=1). Как известно, при соблюдении условия монотонности прямой функции
Как известно, при соблюдении условия монотонности прямой функции 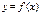 в некотором промежутке
в некотором промежутке 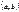 , при обращении ее, получается однозначная обратная функция
, при обращении ее, получается однозначная обратная функция 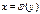 . Если
. Если 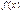 - дифференцируемая функция, то при значениях
- дифференцируемая функция, то при значениях 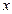 , при которых
, при которых 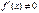 , обратная функция
, обратная функция 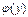 также будет дифференцируемой и производные этих двух функций связаны простым соотношением
также будет дифференцируемой и производные этих двух функций связаны простым соотношением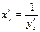 (4.19) т. е. производная обратной функции равна единице, деленной на производную данной функции. (Здесь для ясности, чтобы подчеркнуть аргумент, по которому производится дифференцирование, производные от
(4.19) т. е. производная обратной функции равна единице, деленной на производную данной функции. (Здесь для ясности, чтобы подчеркнуть аргумент, по которому производится дифференцирование, производные от 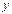 по
по 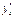 и
и 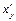 .) Чтобы убедиться в справедливости формулы (4.19), достаточно учесть, что, во-первых,
.) Чтобы убедиться в справедливости формулы (4.19), достаточно учесть, что, во-первых, 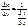 и, во-вторых,
и, во-вторых, 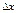 и
и 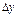 стремятся к нулю одновременно, причем при
стремятся к нулю одновременно, причем при 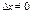 ,
,  , и наоборот [в силу монотонного возрастания или убывания функции
, и наоборот [в силу монотонного возрастания или убывания функции 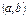 ]. Поэтому
]. Поэтому 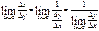 поскольку предположено, что
поскольку предположено, что 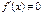 . Мы получили формулу (4.19). Формула дифференцирования обратной функции (4.19) имеет простое геометрическое истолкование. Обе функции, прямая
. Мы получили формулу (4.19). Формула дифференцирования обратной функции (4.19) имеет простое геометрическое истолкование. Обе функции, прямая 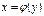 , имеют один и тот же график (см. рис. 4.4). Производная
, имеют один и тот же график (см. рис. 4.4). Производная 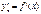 равна (см. § 1, геометрический смысл производной) тангенсу угла
равна (см. § 1, геометрический смысл производной) тангенсу угла 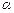 , образованного с осью
, образованного с осью 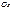 касательной к этому графику в точке М (х;у) с абсциссой
касательной к этому графику в точке М (х;у) с абсциссой 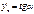 . Точно так же производная
. Точно так же производная 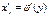 равна тангенсу угла
равна тангенсу угла 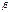 , образованного этой же касательной, но не с осью
, образованного этой же касательной, но не с осью 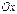 , а с осью
, а с осью 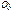 :
: 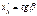 Так как для углов
Так как для углов 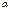 и
и 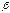 имеем
имеем 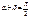 , то
, то 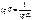 . Отсюда и следует, что
. Отсюда и следует, что  от
от 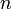 аргументов в окрестности точки
аргументов в окрестности точки 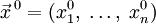 . Для любого единичного вектора
. Для любого единичного вектора 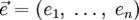 определим производную функции f в точке
определим производную функции f в точке 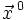 по направлению
по направлению 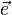 следующим образом:
следующим образом: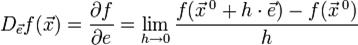
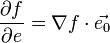 ,
,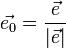 — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора e.
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора e. или
или 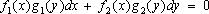
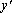 представить в виде отношения дифференциалов
представить в виде отношения дифференциалов 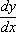 и функция
и функция 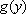 не равна нулю на рассматриваемом интервале, то данное уравнение приводится к виду
не равна нулю на рассматриваемом интервале, то данное уравнение приводится к виду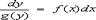
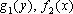 в уравнении (5) не равны нулю, то его можно привести к виду
в уравнении (5) не равны нулю, то его можно привести к виду 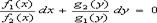
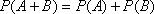
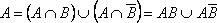
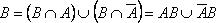 ,
,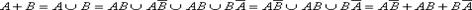
 несовместны, то по аксиоме
несовместны, то по аксиоме 
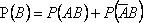
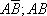 и
и 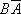 несовместны, по аксиоме
несовместны, по аксиоме 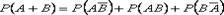
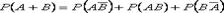
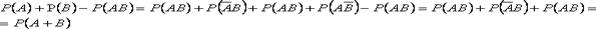
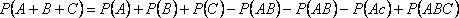
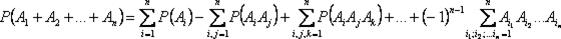 -формула включений и исключений.
-формула включений и исключений.


