
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции, его геометрическая интерпретация, действия над пределами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим числовое множество Или: введем понятие окрестности точки а: так называется любой открытый промежуток с центром в точке а. Теперь можно сказать, что точка «а» будет точкой сгущения множества x, если в каждой ее окрестности содержатся отличные от а значения x из X. Пусть в области x, для которой точка а является точкой сгущения, задана некоторая функция f(x). Представляет интерес поведение этой функции при приближении «x» к «а». Число А называется пределом функции y=f(x) при x стремящемся к а, если для любого e>0 существует число d(e)>0 такое, что при ½x-a½<d(e) выполняем неравенство ½f(x)-A½<e. В этом случае пишут Если область x такова, что в любой близости от а, но справа от а, найдутся отличия от а значение x из x (в этом случае точку а называют правой точкой сгущения), то можно дать определение предела функции, ограничиваясь лишь значением x>a. В этом случае предел функции называется пределом функции f(x) при стремлении x к а справа. Число А называется правосторонним пределом или пределом справа функции f(x) в точке x=a если для "e>0 $ d(e)>0, что при 0<x-a<d(e) выполняется неравенство ½f(x)-A½<e. Пишут Число А называется левосторонним пределом или пределом слева функции f(x) в точках x=a, если для любого e>0 $ d(e)>0, что при 0<а-x<d(e) выполняется неравенство ½f(x)-A½<e. Пишут Число А называется пределом функции y=f(x) при x®¥ если для "e>0 существует число M(e)>0 такое что при ½x½> M(e) выполняется неравенство ½f(x)-A½<e, пишут. Предел функции в некотором смысле может быть сведен к пределу последовательности. Пусть множества x={x} имеет точку сгущения а (а - конечна или бесконечна). Тогда из x (бесконечным множеством способов) можно извлечь, такую последовательность x1, x2, xn … (2) значений x (отличных от а) которая имела бы своим пределом а. Последовательности (2) соответствует последовательность значений функций f(x1), f(x2) …f(xn) (3) При условии равенства (1) эта последовательность всегда имеет предел А (без доказательства). Получим второе определение предела функции. для любой последовательности (2), имеющей пределом а, соответствует последовательность (3), имеющая предел А. Действия над пределами. 1. Если {xn} и {yn} имеют конечные пределы 2. Если {xn} и {yn} имеют конечные пределы: 3. Если {xn} и {yn} имеют конечные пределы: Первый и второй замечательный предел Теорема. Второй замечательный предел Бесконечно малые величины, их свойства, эквивалентность. Функция a(x) называется бесконечно малой при x®a, если Свойства бесконечно малых функций 1. Если функции a1(x) и a2(x) бесконечно малые, то сумма функций a1(x)+ a2(x) также есть бесконечно малая функция. Функция f(x) называется ограниченной при x®a, если существуют положительные числа М и d, такие, что при условии 0<½x-а½<d выполняется неравенство 2. Произведение ограниченной при x®a функции на бесконечно малую, есть функция бесконечно малая. 3. Произведение постоянной на бесконечно малую есть бесконечно малая. 4. Произведение двух бесконечно малых есть бесконечно малая функция. Раскрытие неопределённостей Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют. Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих. Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов
Для раскрытия неопределённостей типа Выявление старшей степени переменной; Деление на эту переменную как числителя, так и знаменателя. Для раскрытия неопределённостей типа Разложение на множители числителя и знаменателя; Сокращение дроби. Для раскрытия неопределённостей типа Пусть
20. Непрерывность функции.Основные определения, теоремы Пусть y=f(x) определена в некотором интервале (а, b), x0 и x – два произвольных значениях аргумента из этого интервала. Обозначим x–x0=Dx откуда x=x0+Dx. Говорят, что для перехода от значения аргумента x0 к значению x, первоначальному значению придано приращение Dx. Приращением Dy функции y=f(x), соответствующем приращению Dx аргумента x в точке x0, называется разность D y=f (x0 +Dx)-f (x0) Определение. Функция y=f(x) называется непрерывной в точке x0, если бесконечно малому приращению Dx аргумента x в точке x0 соответствует бесконечно малое приращение функции D y т.е. Определение. Если функция непрерывна в каждой точке отрезка [а, b], то она непрерывна на этом интервале. Теорема 1. Если функции f1 (x) и f2 (x) непрерывны в точке x0, то непрерывны в этой точке также их алгебраическая сумма f1(x)± f2(x), произведение f1(x) f2(x) и при условии f2(x0)≠0 частное Теорема 2. Если функция u=j(x) непрерывна в точке x0, а функция y=f(u) непрерывна в точке u0=j(x0), то сложная функция y=f(j(x)) непрерывна в точке x0. Точки разрыва Функция f(x) называется непрерывной в точке х0, если: 1) она определена в этой точке; 2) существует Классификация точек разрыва Различают следующие виды разрывов: 1)устранимый разрыв 2)разрыв первого рода или скачок 3)разрыв второго рода Разрывы первого и второго рода неустранимы
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.151 (0.011 с.) |

 . Точка «a» называется точкой сгущения этого множества, если в любой близости от a содержатся значения x из X отличные от a.
. Точка «a» называется точкой сгущения этого множества, если в любой близости от a содержатся значения x из X отличные от a.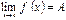 (1)
(1)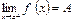
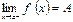 .
.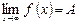

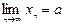
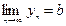 , то и сумма (разность) их также имеет конечный предел,
, то и сумма (разность) их также имеет конечный предел, 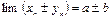
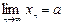
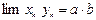

 причем b¹0, то их отношение также имеет конечный предел
причем b¹0, то их отношение также имеет конечный предел  .
. (раскрывает неопределенность типа 0/0).
(раскрывает неопределенность типа 0/0). - иррациональное число.
- иррациональное число. , т.е. если для "e>0 существует d>0, что для всех 0<½x-а½<d, выполняется неравенство ça(x) ç<e. Бесконечно малую функцию ça(x) ç называют также бесконечно малой величиной.
, т.е. если для "e>0 существует d>0, что для всех 0<½x-а½<d, выполняется неравенство ça(x) ç<e. Бесконечно малую функцию ça(x) ç называют также бесконечно малой величиной. .Любая бесконечно малая функция a(x) является ограниченной функцией при x®a.
.Любая бесконечно малая функция a(x) является ограниченной функцией при x®a.









 и
и 

 (аналогично теоремам о пределах).
(аналогично теоремам о пределах). ; 3) этот предел равен значению функции в точке х0, т.е.
; 3) этот предел равен значению функции в точке х0, т.е.  .Если хотя бы одно из этих трёх условий не выполняется, то функция называется разрывной в точке х0, а сама точка х0 называется точкой разрыва функции.
.Если хотя бы одно из этих трёх условий не выполняется, то функция называется разрывной в точке х0, а сама точка х0 называется точкой разрыва функции.


