
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема применения определённого интегралаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
С хема называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»: 1) на отрезке [а;b] выбираем произвольное значение х и рассматриваем переменный отрезок [а; х]. На этом отрезке величина А становится функцией х: А = А(х), т. е. считаем, что часть искомой величины А есть неизвестная функция А(х), где х є [a;b] — один из параметров величины А; 2) находим главную часть приращения ΔА при изменении х на малую величину Δх = dx, т. е. находим дифференциал dA функции А = А(х): dA = ƒ(х) dx, где ƒ(х), определяемая из условия задачи, функция переменной х (здесь также возможны различные упрощения); 3) считая, что dA ≈ ΔА при Δх → 0, находим искомую величину путем интегрирования dA в пределах от а до b:
БИЛЕТ16 Вычисление площади плоских фигур Вычисление площадей с помощью интеграла. 1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a; b ] функции f (x), осью Ох и прямыми х=а и х= b:
2.Площадь фигуры, ограниченной графиками непрерывных функций f (x),
3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и
4.Площадь фигуры, ограниченной графиками непрерывных функций f (x),
БИЛЕТ17 17. Вычисление дуги плоской кривой Пусть известна функция
Для того, чтобы найти длину дуги, нужно вычислить определённый интеграл
БИЛЕТ18 18. Вычисление площади поверхности и объёма тела вращения Указанную площадь можно получить вычислением определенного интеграла:
-Тело образованно вращением вокруг оси абсцисс криволинейной трапеции, расположенно в верхней полуплоскости и ограниченной осью абсцисс, прямыми
БИЛЕТ19 Вопрос 19
БИЛЕТ20 Вопрос 20 Суть метода прямоугольников. Пусть функция y = f(x) непрерывна на отрезке [a; b]. Нам требуется вычислить определенный интеграл Обратимся к понятию определенного интеграла. Разобьем отрезок [a;b] на n частей Суть метода прямоугольников заключается в том, что в качестве приближенного значения определенного интеграла берут интегральную сумму (далее мы покажем, какую именно интегральную сумму берут в методе прямоугольников).
БИЛЕТ21 Вопрос 21 Формула метода трапеций.
Формула метода Симпсона (парабол) имеет вид Графическая иллюстрация метода парабол (Симпсона). Красной линией изображен график функции y=f(x), синей линией показано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке разбиения.
БИЛЕТ22 Исследование пределов и непрерывности в многомерных пространствах приводит ко многим нелогичным и патологическим результатам, не свойственным функциям одной переменной. Например, существуют скалярные функции двух переменных, имеющих точки в области определения, которые при приближении вдоль произвольной прямой дают специфический предел, и дают другой предел при приближении вдоль параболы. Функция
стремится к нулю по любой прямой, проходящей через начало координат. Однако, когда к началу координат приближаются вдоль параболы
Функция Функция Функция
БИЛЕТ23 Вопрос 23 Частная производная обобщает понятие производной на случай нескольких измерений. Частная производная функции нескольких переменных — это производная относительно одной переменной, все другие переменные при нахождении считаются константами. Для упрощения ограничимся случаем функций от трех переменных; все дальнейшее, однако, справедливо и для функций любого числа переменных. Пусть в некоторой области Аналогично определяются и частные производные функции Дифференциальные уравнения, содержащие частные производные, называют дифференциальными уравнениями в частных производных или (Д)УЧП. Эти уравнения как правило сложнее для решения чем обычные дифференциальные уравнения, которые содержат производные относительно только одной переменной.
БИЛЕТ24 Вопрос 24 Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют)
и, аналогично,
Производные
БИЛЕТ25 25. Дифференцируемость и полный дифференциал функции двух переменных. Теорема о равенстве смешанных производных высших порядков.
Пусть функция Функция
где Главная часть приращения функции
Выражения
Теорема 1 (необходимое условие дифференцируемости функции). Если функция Так как функция дифференцируема в точке М, то имеет место равенство (1). Отсюда вытекает, что Это означает, что функция непрерывна в точке М. Положив
Равенство (1) можно записать в виде
где
Отметим, что обратное утверждение не верно, т. е. из непрерывности функции или существования частных производных не следует дифференцируемость функции. Так, непрерывная функция Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (3) принимает вид:
или
где Теорема 2 (достаточное условие дифференцируемости функции).Если функция Отметим, что для функции Чтобы функция Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциала функции двух (и большего числа) переменных. Из определения дифференциала функции
Так как полное приращение
Формулой (7) пользуются в приближенных расчетах. Отметим, что с помощью полного дифференциала можно найти: границы абсолютной и относительной погрешностей в приближенных вычислениях; приближенное значение полного приращения функции и т. д. Теорема: Если в некоторой окрестности точки
БИЛЕТ26 26. Пусть функция
Аналогично определяются дифференциалы более высоких порядков. Определение: Дифференциалом Сложная функция – это функция, аргументом которой также является функция. С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)). К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а В свою очередь, g(x) также может быть сложной функцией. Например, Часто можно слышать, что сложную функцию называют композицией функций. Формула нахождения производной сложной функции:
БИЛЕТ27 27. Пусть имеется поверхность, заданная уравнением
Прямая, проведенная через точку поверхности, перпендикулярно к касательной плоскости называется нормалью к поверхности.
Если поверхность задана уравнением
а уравнение нормали к поверхности в этой же точке – в виде:
БИЛЕТ28 28. Пусть функция F(t) в некоторой окрестности V(t0) имеет производные до (n+1)-го порядка включительно. Тогда справедлива формула Тейлора:
Обозначим t-t0=Δt, F(t)-F(t0)=ΔF(t0), F'(t0)(t-t0)=F'(t0)Δt=dF(t0), F''(t0)(t-t0)2=F''(t0)(Δt)2=d2F(t0) и т.д. Геометрический смысл теоремы Ролля Курс лекций по математике Тогда (8) можно записать в виде
, где 0<θ<1. (9) В виде (9) формула Тейлора распространяется и на случай функций нескольких переменных.
Теорема. Пусть функция z=f(x;y), где х, у – независимые переменные, определена и имеет непрерывные частные производные до (n+1)-го порядка включительно в некоторой окрестности точки М(х0;y0) Vδ(х0;y0). Тогда "Δх, Δу, удовлетворяющих условию
где 0<θ<1. (10) Доказательство. Зафиксируем Δх, Δу:
Тогда ММ0ÎVδ(х0;y0). Параметрические уравнения отрезка ММ0:
Функция на [0;1] становится сложной функцией от переменной t:
f(x;y)=f(х0+tΔx;y0+tΔy)=F(t). (12)
По условию f(x;y) имеет непрерывные частные производные до (n+1)-го порядка включительно на Vδ(х0;y0). Функции х и у, как линейные, имеют непрерывные производные любого порядка. Поэтому F(t) имеет непрерывные производные до (n+1)-го порядка включительно на [0;1]. Тогда для F(t) на [0;1] справедлива формула Тейлора (9).Положим в ней t0=1, t0+Δt=1, Δt=1:
Перейдем здесь к f(x;y), используя (12).
ΔF(0)=F(1)-F(0)=f(х0+Δx;y0+Δy)-f(х0;y0)=Δf(х0;y0).
Форма первого дифференциала инвариантна. Тогда, учитывая (11) при вычислении dx и dy, получим
Поскольку х=х0+tΔx, y=y0+tΔy – линейные функции, то дифференциалы высших порядков от функции F(t)=f(x;y) обладают свойством инвариантности.. Следовательно, для их вычисления мы можем использовать простейшую форму:
Аналогично,
Подставляя все выражения в (13), получим (10).
Формула Тейлора имеет большое значение при вычислении приращений и значений функции с большой степенью точности.
БИЛЕТ29 29. Говорят, что функция Говорят, что функция Максимум и минимум функции называются экстремумами функции. Теорема (необходимое условие экстремума функции двух переменных). Если функция Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку тогда при 1) 2) 3) 4) если
БИЛЕТ30 30. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ— математический (математико-статистический) прием, служащий для выравнивания динамических рядов, выявления формы корреляционной связи между случайными величинами и др. Состоит в том, что функция, описывающая данное явление, аппроксимируется более простой функцией. Причем последняя подбирается с таким расчетом, чтобы среднеквадратичное отклонение фактических уровней функции в наблюдаемых точках от выровненных было наименьшим. Напр., по имеющимся данным (xi,yi) (i = 1, 2,..., n) строится такая кривая y = a + bx, на которой достигается минимум суммы квадратов отклонений
т. е. минимизируется функция, зависящая от двух параметров: a — отрезок на оси ординат и b — наклон прямой. Уравнения, дающие необходимые условия минимизации функции S(a,b), называются нормальными уравнениями. В качестве аппроксимирующих функций применяются не только линейная (выравнивание по прямой линии), но и квадратическая, параболическая, экспоненциальная и др.
БИЛЕТ37 37 приложения двойного интэграла
Пусть тело V ограничено (рис. 2.12) сверху — только одной поверхностью При этих условиях:
Доказательство формулы (2.17) легко провести на основе геометрического смысла двойного интеграла.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.84.174 (0.014 с.) |



 и прямыми х=а, х= b:
и прямыми х=а, х= b:


 и требуется найти длину дуги, заданной функцией
и требуется найти длину дуги, заданной функцией  .
.
 , где
, где 
 и
и  и графиком непрерывной функции
и графиком непрерывной функции  .
.
 . (1)
. (1)
 . (2)
. (2)
 . (3)
. (3)
 . (4)
. (4)
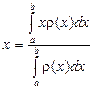 . (5)
. (5)
 . (6)
. (6)
 . (7)
. (7)
 .
. точками
точками  . Внутри каждого отрезка
. Внутри каждого отрезка  . Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения
. Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения  , то любая из интегральных сумм является приближенным значением интеграла
, то любая из интегральных сумм является приближенным значением интеграла  .
.
 .
.
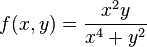
 , предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует.
, предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует. имеет пределом число A при стремлении переменных
имеет пределом число A при стремлении переменных  , соответственно, к
, соответственно, к  , если для каждого число
, если для каждого число  найдется такое число
найдется такое число  , что
, что  , то есть
, то есть  .
. называется непрерывной в точке
называется непрерывной в точке  , если предельное значение этой функции в точке
, если предельное значение этой функции в точке  .
. , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества. имеем функцию
имеем функцию  ; возьмем точку
; возьмем точку  в этой области. Если мы будем считать
в этой области. Если мы будем считать  и
и  за постоянные значения
за постоянные значения  и
и  , и будем менять
, и будем менять  , то
, то  будет функцией от одной переменной
будет функцией от одной переменной  ); можно поставить вопрос о вычислении ее производной в точке
); можно поставить вопрос о вычислении ее производной в точке  . Придадим этому значению
. Придадим этому значению  , тогда функция получит приращение
, тогда функция получит приращение  , которое можно было бы назвать ее частным приращением (по
, которое можно было бы назвать ее частным приращением (по  . Эта производная называется частной производной функции
. Эта производная называется частной производной функции  по
по  .
. ) используется для определения понятий градиента, дивергенции, и ротора с точки зрения частных производных. Матрица частных производных — матрица Якоби — может использоваться для представления производной функции (отображения) между двумя пространствами произвольной размерности. Таким образом производная может быть представлена как линейное преобразование, которое изменяется в зависимости от точки из области определения функции.
) используется для определения понятий градиента, дивергенции, и ротора с точки зрения частных производных. Матрица частных производных — матрица Якоби — может использоваться для представления производной функции (отображения) между двумя пространствами произвольной размерности. Таким образом производная может быть представлена как линейное преобразование, которое изменяется в зависимости от точки из области определения функции. и
и  , которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная
, которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная 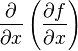 обозначается через
обозначается через  или
или  , а
, а  через
через  или
или  . Таким образом,
. Таким образом,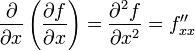 ,
, 
 ,
,  .
. и
и  называются частными производными второго порядка. Определение: Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D,называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные 3 порядка:
называются частными производными второго порядка. Определение: Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D,называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные 3 порядка:  ,
,  ,
,  и т. д.
и т. д. определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Составим полное приращение функции в точке М:
. Составим полное приращение функции в точке М: 
 (1)
(1)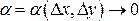 и
и  при
при  . Сумма первых двух слагаемых в равенстве (1) представляет собой главную часть приращения функции..
. Сумма первых двух слагаемых в равенстве (1) представляет собой главную часть приращения функции.. и
и  :
: (2)
(2) и
и  называют частными дифференциалами. Для независимых переменных х и у полагают
называют частными дифференциалами. Для независимых переменных х и у полагают  и
и  . Поэтому равенство (2) можно переписать в виде
. Поэтому равенство (2) можно переписать в виде (3)
(3) и
и  , причем
, причем 


 в равенстве (1), получим:
в равенстве (1), получим:  Отсюда находим
Отсюда находим  Переходя к пределу при
Переходя к пределу при  т. е.
т. е.  Таким образом, в точке М существует частная производная
Таким образом, в точке М существует частная производная  Аналогично показывается, что в точке М существует частная производная
Аналогично показывается, что в точке М существует частная производная 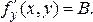
 (4)
(4) при
при  не дифференцируема в точке (0;0).
не дифференцируема в точке (0;0). (5)
(5)

 – частные дифференциалы функции
– частные дифференциалы функции  и
и  в точке М(х, у), то она дифференцируема в этой точке и её полный дифференциал выражается формулой (5).
в точке М(х, у), то она дифференцируема в этой точке и её полный дифференциал выражается формулой (5). одной переменной существование производной
одной переменной существование производной  в точке является необходимым и достаточным условием её дифференцируемости в этой точке.
в точке является необходимым и достаточным условием её дифференцируемости в этой точке. и
и  имеет место приближенное равенство
имеет место приближенное равенство (6)
(6) равенство (6) можно переписать в следующем виде:
равенство (6) можно переписать в следующем виде: (7)
(7) функция
функция  имеет смешанные частные производные
имеет смешанные частные производные  и
и  , причём эти смешанные частные производные непрерывны в точке
, причём эти смешанные частные производные непрерывны в точке  , то они равны в этой точке:
, то они равны в этой точке: 

 зависит от переменной
зависит от переменной  и дифференцируема в точке
и дифференцируема в точке  , рассматриваемый как функция от
, рассматриваемый как функция от  данной функции, который называется дифференциалом второго порядка функции
данной функции, который называется дифференциалом второго порядка функции 
 -го порядка
-го порядка  функции
функции  -го порядка этой функции, то есть
-го порядка этой функции, то есть 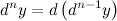
 - целая рациональная функция, тогда
- целая рациональная функция, тогда 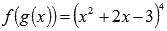 .
. . Условно такое выражение можно обозначить как
. Условно такое выражение можно обозначить как  . Здесь f – функция синуса, - функция извлечения квадратного корня,
. Здесь f – функция синуса, - функция извлечения квадратного корня,  - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом
- дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом  .
.
 . Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку
. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку  , называется касательной плоскостью к поверхности в точке
, называется касательной плоскостью к поверхности в точке  .
.


 (8)
(8)
 , имеет место формула Тейлора:
, имеет место формула Тейлора: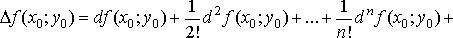

 , где
, где  .
. 
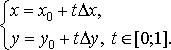 (11)
(11) (13)
(13)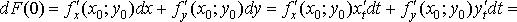
 т.к. dt=Δt=1.
т.к. dt=Δt=1.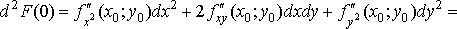

 ,…,
,…,  ,
,
 имеет максимум в точке
имеет максимум в точке 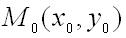 , т.е. при
, т.е. при  , если
, если  для всех точек
для всех точек 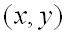 , достаточно близких к точке
, достаточно близких к точке  и отличных от неё.
и отличных от неё. для всех точек
для всех точек  или обращается в нуль при этих значениях аргументов, или не существует.
или обращается в нуль при этих значениях аргументов, или не существует.
 имеет максимум, если дискриминант
имеет максимум, если дискриминант  и
и  где
где 
 ;
;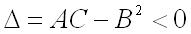 ;
; , то экстремум может быть, а может и не быть (требуется дополнительное исследование).
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).

 2. Вычисление объёмов тел
2. Вычисление объёмов тел



