
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр масс и моменты инерции кривойСодержание книги Поиск на нашем сайте
Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности ρ (x,y,z). Тогда координаты центра масс кривой определяются формулами
где
− так называемые моменты первого порядка. Моменты инерции относительно осей Ox, Oy и Oz определяются формулами
Работа поля Работа при перемещении тела в силовом поле
где Заметим, что силовое поле Если векторное поля задано в координатной форме в виде
то работа поля вычисляется по формуле
В частном случае, когда тело двигается вдоль плоской кривой C в плоскости O xy, справедлива формула
где Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид
где t изменяется в интервале от α до β. Если векторное поле
где
Закон Ампера Криволинейный интеграл от магнитного поля с индукцией
где Закон Фарадея Электродвижущая сила ε, наведенная в замкнутом контуре C, равна скорости изменения магнитного потока ψ, проходящего через данный контур (рисунок 3).
БИЛЕТ51. ОПРЕДЕЛЕНИЕ. Число Если существует конечный предел интегральных сумм Поверхностный интеграл I рода от функции
( Если существует Достаточное условие существования поверхностного интеграла I рода будет сформулировано позже, когда покажем способ его вычисления. Определение поверхностного интеграла I рода по структуре такое же, как и определение определенного интеграла. Поэтому поверхностный интеграл I рода обладает теми же свойствами, что и определенный интеграл. Приведем эти свойства без доказательства. СВОЙСТВА ПОВЕРХНОСТНОГО ИНТЕГРАЛА I РОДА 1. 2. Постоянный множитель можно выносить за знак поверхностного интеграла I рода, т.е. 3. Поверхностный интеграла I рода от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме поверхностных интегралов I рода от этих функций, т.е.
4. Если поверхность
(свойство аддитивности поверхностного интеграла I рода). 5. Если всюду на поверхности 6. Если всюду на поверхности
то 7. (следствие свойств 6 и 1) Если
где 8. (теорема о среднем для поверхностного интеграла I рода) Если функция
где
БИЛЕТ52 Рассмотрим скалярную функцию
где координаты (u,v) изменяются в пределах некоторой области определения
Поверхностный интеграл первого рода от функции
где частные производные
а Абсолютное значение
Площадь поверхности S выражается с помощью поверхностного интеграла в виде
Если поверхность S задана уравнением
Если поверхность S состоит из нескольких частей Si, то для вычисления поверхностного интеграла можно использовать свойство аддитивности:
Сила давления Предположим, что поверхность S задана вектором
Давление, по определению, действует в направлении вектора нормали к поверхности S в каждой точке. Поэтому, мы можем записать
где
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1020; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |




 вдоль кривой C выражается через криволинейный интеграл второго рода
вдоль кривой C выражается через криволинейный интеграл второго рода
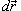 − единичный касательный вектор (рисунок 1). Обозначение
− единичный касательный вектор (рисунок 1). Обозначение  означает скалярное произведение векторов
означает скалярное произведение векторов 


 .
.

 − потенциал поля.
− потенциал поля.

 вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой
вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой
 - магнитная проницаемость ваккуума, равная
- магнитная проницаемость ваккуума, равная  Н/м.
Н/м.

 называется пределом интегральных сумм
называется пределом интегральных сумм 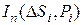 при
при  (обозначают
(обозначают  ), если для любого
), если для любого  существует
существует  такое, что для любого разбиения поверхности
такое, что для любого разбиения поверхности  у которого
у которого  , при любом выборе точек
, при любом выборе точек 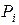 выполняется неравенство
выполняется неравенство  .
. по поверхности
по поверхности 
 – переменные интегрирования,
– переменные интегрирования,  – дифференциал площади поверхности).
– дифференциал площади поверхности). , где
, где  – площадь поверхности
– площадь поверхности  .
.

 .
. и
и 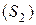 , не имеющие общих внутренних точек, то
, не имеющие общих внутренних точек, то

 (
( ), то
), то  (
(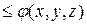 ),
),
 .
. и
и  – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции 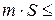
 ,
,
 , что справедливо равенство
, что справедливо равенство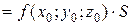 ,
, и поверхность S. Пусть S задана векторной функцией
и поверхность S. Пусть S задана векторной функцией
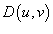 в плоскости uv. Заметим, что функция
в плоскости uv. Заметим, что функция 
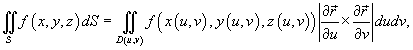
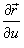 и
и  равны
равны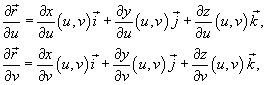
 означает векторное произведение. Вектор
означает векторное произведение. Вектор  .
. называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1).
называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1).


 , где z (x,y) − дифференцируемая функция в области D (x,y), то поверхностный интеграл находится по формуле
, где z (x,y) − дифференцируемая функция в области D (x,y), то поверхностный интеграл находится по формуле
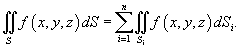
 , где S − часть плоскости
, где S − часть плоскости  , лежащая в первом октанте (x ≥ 0, y ≥ 0, z ≥ 0).
Решение.
Запишем уравнение плоскости в виде
, лежащая в первом октанте (x ≥ 0, y ≥ 0, z ≥ 0).
Решение.
Запишем уравнение плоскости в виде
 Найдем частные производные
Найдем частные производные
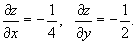 Применяя формулу
Применяя формулу
 поверхностный интеграл можно выразить через двойной интеграл:
поверхностный интеграл можно выразить через двойной интеграл:
 Область интегрирования D представляет собой треугольник, показанный выше на рисунке 2. Вычисляем окончательно заданный интеграл:
Область интегрирования D представляет собой треугольник, показанный выше на рисунке 2. Вычисляем окончательно заданный интеграл:
 БИЛЕТ53.
Поверхностные интегралы применяются во многих прикладных расчетах. В частности, с их помощью вычисляются
· Масса оболочки;
· Центр масс и моменты инерции оболочки;
· Сила притяжения и сила давления;
· Поток жидкости и вещества через поверхность;
· Электрический заряд, распределенный по поверхности;
· Электрические поля (теорема Гаусса в электростатике).
Масса оболочки
Пусть S представляет собой тонкую гладкую оболочку. Распределение массы оболочки описывается функцией плотности
БИЛЕТ53.
Поверхностные интегралы применяются во многих прикладных расчетах. В частности, с их помощью вычисляются
· Масса оболочки;
· Центр масс и моменты инерции оболочки;
· Сила притяжения и сила давления;
· Поток жидкости и вещества через поверхность;
· Электрический заряд, распределенный по поверхности;
· Электрические поля (теорема Гаусса в электростатике).
Масса оболочки
Пусть S представляет собой тонкую гладкую оболочку. Распределение массы оболочки описывается функцией плотности  . Тогда полная масса оболочки выражается через поверхностный интеграл первого рода по формуле
. Тогда полная масса оболочки выражается через поверхностный интеграл первого рода по формуле
 Центр масс и моменты инерции оболочки
Пусть распределение массы m в тонкой оболочке описывается непрерывной функцией плотности
Центр масс и моменты инерции оболочки
Пусть распределение массы m в тонкой оболочке описывается непрерывной функцией плотности  где
где
 − так называемые моменты первого порядка относительно координатных плоскостей x = 0, y = 0 и z = 0, соответственно. Моменты инерции оболочки относительно осей Ox, Oy, Oz выражаются, соответственно, формулами
− так называемые моменты первого порядка относительно координатных плоскостей x = 0, y = 0 и z = 0, соответственно. Моменты инерции оболочки относительно осей Ox, Oy, Oz выражаются, соответственно, формулами
 Моменты инерции оболочки относительно плоскостей xy, yz, xz определяются формулами
Моменты инерции оболочки относительно плоскостей xy, yz, xz определяются формулами
 Сила притяжения поверхности
Пусть задана поверхность S, а в точке (x 0, y 0, z 0), не принадлежащей поверхности, находится тело массой m (рисунок 1).
Сила притяжения поверхности
Пусть задана поверхность S, а в точке (x 0, y 0, z 0), не принадлежащей поверхности, находится тело массой m (рисунок 1).



 , G - гравитационная постоянная,
, G - гравитационная постоянная, 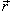 и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила
и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила  , находится с помощью поверхностного интеграла по формуле
, находится с помощью поверхностного интеграла по формуле

 − единичный нормальный вектор к поверхности S.
− единичный нормальный вектор к поверхности S. 


