
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства определенного интегралаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
БИЛЕТ11
БИЛЕТ12 12. Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий. · Область интегрирования является бесконечной. Например, является бесконечным интервалом · Функция f(x) неограничена в области интегрирования. Если интервал [a,b] конечный, и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла. Несобственные интегралы I рода Пусть 1. Если 2. Если не существует конечного Пусть 1. Если 2. Если не существует конечного Если функция
Геометрический смысл несобственного интеграла I рода Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции. Примеры
БИЛЕТ13 Несобственный интеграл второго рода Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции Несобственным интегралом второго рода назовём определенный интеграл
значение которого равняется левостороннему пределу
14. Признаки сходимости несобственных интегралов Первая теорема сравнения
Если
Если При При
Если
Если
Если f имеет ограниченную первообразную на БИЛЕТ15
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.133.251 (0.008 с.) |

 , где х, t – любые буквы.
, где х, t – любые буквы.




 , где
, где  непрерывна на
непрерывна на 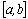 . Введем новую переменную
. Введем новую переменную  , связанную с
, связанную с  равенством
равенством  . Если
1)
. Если
1)  2)
2)  и
и  непрерывны на
непрерывны на  ,
3) при изменении z от α до β значения
,
3) при изменении z от α до β значения  то
то

 –первообразная для функции
–первообразная для функции  . Тогда по формуле Ньютона–Лейбница
. Тогда по формуле Ньютона–Лейбница
 является первообразной для функции
является первообразной для функции  :
:  =[по правилу дифференцирования сложной функции] =
=[по правилу дифференцирования сложной функции] =  Тогда по формуле Ньютона–Лейбница
Тогда по формуле Ньютона–Лейбница

 при x = ln 2
при x = ln 2 
 =
= 
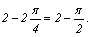

 Пример.
Пример.

 .
. определена и непрерывна на множестве от
определена и непрерывна на множестве от 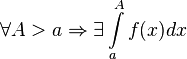 . Тогда:
. Тогда: , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  (
( или
или  ), то интеграл
), то интеграл  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся. и
и  . Тогда:
. Тогда: , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  (
( называется расходящимся к
называется расходящимся к  , где с — произвольное число.
, где с — произвольное число.


 на
на  то из сходимости
то из сходимости  следует сходимость,
следует сходимость, 
 то при
то при  интегралы
интегралы  из сходимости
из сходимости  из сходимости
из сходимости  при
при  то при
то при  интеграл
интеграл  то
то  сходится.
сходится.



