
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральное исчисление функций одной переменнойСодержание книги
Поиск на нашем сайте
Интегральное исчисление функций одной переменной Первообразная функция, ее свойства. Определение неопределенного интеграла, его простейшие свойства. Первообразной функции Её свойства: 1) Пусть (F(x)+C)'=F'(x)=f(x) 2) Если Доказательство: Неопределенный интеграл - множество первообразных данной функции Его свойства: 1) Производная неопределенного интеграла равна подынтегральной функции, т.е. F’(x)=f(x), то и 2) Дифференциал от неопределенного интеграла равен подынтегральному выражению: 3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная: 4) Постоянный множитель можно выносить за знак интеграла, т.е. 5) Неопределенный интеграл от суммы двух или нескольких функций равен сумме их интегралов, т.е.
6) Если Действительно,
2. Интегралы некоторых элементарных функций (таблица интегралов).
Метод подстановки или замена переменной в неопределенном интеграле.
Интегрирование по частям в неопределенном интеграле.
Разложение правильной рациональной дроби в сумму простейших дробей.
Любой многочлен с действительными коэффициентами можно записать в виде:
Простейшие дроби называются функции двух видов: 1) 2) Всякая правильная дробь представима, причем единственным образом, в виде суммы простейших дробей.
Алгоритм и интегрирования рациональных дробей. Алгоритм взятия интеграла вида 2) Знаменатель дроби разложить на множители. 3) Представить правильную дробь в виде суммы простейших дробей. 4) Проинтегрировать простейшие дроби. Интегралы от простейших (элементарных дробей). 8. Интегралы вида Вычисление неопределенных интегралов вида
Другие подстановки: 1)Интегралы типа а) подстановка б) в) формулы понижения степени г) 2) тригонометрические преобразования 3) дробно-линейная подстановка 9. Интегрирование некоторых иррациональных выражений. Интегралы вида:
10. Тригонометрические и гиперболические подстановки. Интегралы вида:
Интегрирование дифференциального бинома.
Теорема П.Л.Чебышева. Интеграл от дифференциального бинома выражается через элементарные функции только в трех случаях. 1) Если p -целое. 2) Если 3) Рассмотрим подробно эти случаи: 1) Если p-целое. Если обозначим через r-наименьшее общее кратное знаменателей рациональных чисел m и n, то получим:
Пусть p- дробное число. Сделаем замену 2) Пусть
3)
s- знаменатель числа p. Замена
Теорема об оценке. Формула Ньютона-Лейбница. Если функция f(x) непрерывна на отрезке [a;b], а функция F(x) является первообразной для f(x) на [a;b], то справедлива формула
î Согласно теореме о дифференцировании интеграла по верхнему пределу, функция
Положив в этом равенстве сначала x=a, а затем x=b, получим Но Ф(a)=0 и Свойства сходящихся рядов. Пусть даны два ряда с положительными членами: Тогда 1) Если сходится (2), то сходится и (1). 2) Если расходится (1), то расходится и (2). Доказательство: Докажем сначала первую часть. Положим Признак Даламбера. Пусть для ряда Тогда если q<1 то ряд сходится, а если q>1, то ряд расходится. Доказательство: По определению предела для любого Пусть теперь q>1. тогда выбрав Радикальный признак Коши. Пусть дан ряд Доказательство: Рассмотрим криволинейную трапецию ограниченную линией 1) несобственный интеграл сходится, т.е. 2) интеграл расходится; тогда Интегральный признак Коши.
Un=f(n); f(x) монотонно убывает на (1;¥)
In<f(1)+f(2)+…+f(n-1)=Sn-1 In>f(2)+f(3)+…+f(n)=Sn-U1 Sn-U1<In<Sn+Un Пусть интеграл сходится, In<I "n Sn<In+U1<I+U1 Ограниченная сверху монотонно возрастающая последовательность Пусть Sn>In+Un – также неограниченно возрастающая последовательность => ряд расходится. Приложения степенных рядов. Ряд вида
Функции многих переменных 47. Понятие функции многих переменных, область определения, график (n =2). Функцией 2-х переменных, определенной на мн-ве DcR2, называется закон сопоставляющий каждой точке с координатами Множество совокупностей значение переменной называют областью определения ф-ции. Геометрической интерпретацией функции двух переменных f(x,y) служит поверхность z=f(x,y), которую называют графиком этой функции. Например, если
Полная производная. Пусть z=ƒ(x;y) – функция двух переменных х и у, каждая из которых является функцией независимой переменной t: x=x(t), y=y(t). В этом случае функция z=ƒ(x(t);y(t)) является сложной функцией одной переменной t; переменный х и у – промежуточные переменные. Теорема. Если z=ƒ(x;y) – дифференцируема в точке М(х;у)
Частный случай: z=ƒ(x;y), где у=у(х), т.е. z=ƒ(x;y(х)) – сложная функция одной независимой переменной х. Согласно формуле (1) имеем:
Формулу (2) носит название формулы полной производной. Общий случай: z=ƒ(x;y), где x=x(u;v), y=y(u;v). Тогда z=ƒ(x(u;v); y(u;v)) – сложная функция независимых переменных u и v. Ее частные производные
Аналогично получаем: Таким образом, производная сложной функции (z) по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (u и v) на их производные по соответствующей независимой переменной (u и v)
57. Полный дифференциал 1–го порядка сложной функции, свойство инвариантности. Дифференциал сложной функции порядка выше 1–го, нарушение свойства инвариантности. Уравнение Бернулли Найти решение задачи Коши для уравнение Бернулли
С начальным условием
Решение
Где р=(1-α)g и q=(1-α)ƒ 2. решаем линейное уравнение (2) и делаем замену z=y1-α. 3. Используем начальное условие (1′), находим решение поставленной задачи Коши. Записываем ответ в виде у=φ(х) ЗАМЕЧАНИЕ. При решении уравнения Бернулли можно не приводить к линейному, а искать решение в виде y=u(x)v(x) или применять метод вариации произвольной постоянной.
Интегральное исчисление функций одной переменной
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.27 (0.01 с.) |

 называется такая функция
называется такая функция  , что
, что  =
=  .
. непрерывна, F(x) –первообразная
непрерывна, F(x) –первообразная  F(x)+C
F(x)+C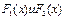 две первообразные для функции
две первообразные для функции  на отрезке [a,b], то разность между ними равна постоянному числу.
на отрезке [a,b], то разность между ними равна постоянному числу.



 или
или 
 , где а- некоторая постоянная. Действительно, в силу свойства 1) неопределенного интеграла
, где а- некоторая постоянная. Действительно, в силу свойства 1) неопределенного интеграла  и
и  , т.е. выражения
, т.е. выражения 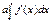 и
и  являются неопределенными интегралами для одной и той же функции
являются неопределенными интегралами для одной и той же функции  . Следовательно, они равны (в том смысле, что выражают одно и то же множество функций).
. Следовательно, они равны (в том смысле, что выражают одно и то же множество функций). . Доказательство: Как и в предыдущем случае, найдем производные левой и правой частей равенства:
. Доказательство: Как и в предыдущем случае, найдем производные левой и правой частей равенства: ,
,  Таким образом, производные от левой и правой частей равенства равны между собой. Следовательно, выражения
Таким образом, производные от левой и правой частей равенства равны между собой. Следовательно, выражения  и
и 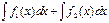 представляют собой совокупность всех первообразных для одной и той же функции
представляют собой совокупность всех первообразных для одной и той же функции  . Значит они равны.
. Значит они равны. , то
, то  .
. . Обозначим через
. Обозначим через  и вспомнив правило вычисления производной сложной функции, имеем
и вспомнив правило вычисления производной сложной функции, имеем  .
.



 , где
, где  и
и  -многочлены от х.
-многочлены от х. дробь правильная
дробь правильная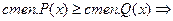 дробь неправильная, тогда
дробь неправильная, тогда  , где
, где  -многочлен, а
-многочлен, а  -правильная дробь.
-правильная дробь.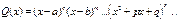


 -неизвестные коэффициенты
-неизвестные коэффициенты
 : 1) если дробь неправильная выделить целую часть
: 1) если дробь неправильная выделить целую часть . Универсальная подстановка и другие подстановки.
. Универсальная подстановка и другие подстановки. сводится к вычислению интегралов от рациональной функции подстановкой
сводится к вычислению интегралов от рациональной функции подстановкой  , которая называется универсальной.
, которая называется универсальной.
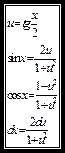
 .
. , если n-целое положительное нечетное число;
, если n-целое положительное нечетное число; , если m-целое положительное нечетное число
, если m-целое положительное нечетное число , если m+n-есть четное отрицательное число
, если m+n-есть четное отрицательное число и
и  .
.
 , здесь m,n,p-рациональные числа.
, здесь m,n,p-рациональные числа.

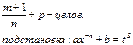

 .
. - целое число
- целое число . Используя замену
. Используя замену  , получаем:
, получаем:

 целое число.
целое число.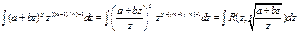
 сводит интеграл
сводит интеграл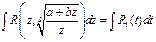 к интегралу от рациональной функции t
к интегралу от рациональной функции t
 есть первообразная для функции f(x) на отрезке [a;b]. Так как и функция F(x) является первообразной для f(x) на [a;b], то разность Ф(x)-F(x) равна некоторой постоянной C на всем отрезке [a;b], т.е.
есть первообразная для функции f(x) на отрезке [a;b]. Так как и функция F(x) является первообразной для f(x) на [a;b], то разность Ф(x)-F(x) равна некоторой постоянной C на всем отрезке [a;b], т.е.

 .
. , т.е.
, т.е.  и, следовательно,
и, следовательно,  J
J и пусть каждый член ряда (1) не больше соответствующего члена ряда (2), т.е.
и пусть каждый член ряда (1) не больше соответствующего члена ряда (2), т.е.  (n=1,2,3…).(*)
(n=1,2,3…).(*) и
и  по условию ряд (2) сходится, поэтому
по условию ряд (2) сходится, поэтому  , где
, где 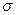 -сумма второго ряда. А из условия (*) следует что
-сумма второго ряда. А из условия (*) следует что  , т.е. что частичные суммы ряда (1) ограничены сверху. Но тогда в силу леммы(Если частичные суммы ряда с положительными членами ограничены сверху
, т.е. что частичные суммы ряда (1) ограничены сверху. Но тогда в силу леммы(Если частичные суммы ряда с положительными членами ограничены сверху 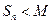 , то ряд сходится) ряд сходится. Для доказательства второй части достаточно заметить что поскольку ряд (1) расходится, его частичные суммы неограниченно возрастают:
, то ряд сходится) ряд сходится. Для доказательства второй части достаточно заметить что поскольку ряд (1) расходится, его частичные суммы неограниченно возрастают:  . Так как
. Так как  , то и
, то и 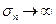 , а следовательно ряд (2) сходится, что и требовалось доказать.
, а следовательно ряд (2) сходится, что и требовалось доказать. с неотрицательными членами выполняется условие
с неотрицательными членами выполняется условие  .
.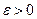 существует номер N такой, что
существует номер N такой, что  при любом
при любом  . Пусть q<1. Тогда выбрав
. Пусть q<1. Тогда выбрав  , из неравенства (
, из неравенства (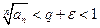 при любом
при любом  при любом
при любом  , из неравенства (
, из неравенства ( при любом
при любом 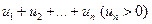 , члены которого являются значениями непрерывной функции f(x) при целых значениях аргумента x:
, члены которого являются значениями непрерывной функции f(x) при целых значениях аргумента x: 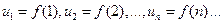 , и пусть f(x) монотонно убывает в интервале
, и пусть f(x) монотонно убывает в интервале  . Тогда ряд сходится если сходится несобственный интеграл
. Тогда ряд сходится если сходится несобственный интеграл  и расходится если этот интеграл расходится.
и расходится если этот интеграл расходится.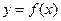 с основанием от x=1 до x=n, где n-произвольное целое положительное число. Площадь ее измеряется интегралом
с основанием от x=1 до x=n, где n-произвольное целое положительное число. Площадь ее измеряется интегралом  .отметим целые точки основания x=1,x=2,…,x=n-1,x=n. Рассмотрим площадь ступенчатой фигуры: одна из них (входящая) имеет площадь равную
.отметим целые точки основания x=1,x=2,…,x=n-1,x=n. Рассмотрим площадь ступенчатой фигуры: одна из них (входящая) имеет площадь равную 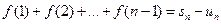 где
где  . Площадь первой фигуры меньше площади данной криволинейной трапеции, площадь второй больше ее, т.е. мы имеем
. Площадь первой фигуры меньше площади данной криволинейной трапеции, площадь второй больше ее, т.е. мы имеем  . Отсюда получаем два неравенства:
. Отсюда получаем два неравенства:  (*) и
(*) и 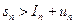 (**). Так как функция
(**). Так как функция  возрастает вместе с n; возможны 2 случая:
возрастает вместе с n; возможны 2 случая: существует; тогда
существует; тогда  и из неравенства (*) при всяком n находим
и из неравенства (*) при всяком n находим  . Следовательно частичные суммы
. Следовательно частичные суммы  ограничены и на основании леммы(если частичные суммы ряда с положительными членами ограничены сверху, то ряд сходится) ряд сходится.
ограничены и на основании леммы(если частичные суммы ряда с положительными членами ограничены сверху, то ряд сходится) ряд сходится. при
при  и на основании неравенства (**) заключаем, что
и на основании неравенства (**) заключаем, что  Пусть дан ряд
Пусть дан ряд  , Un>0 " n.
, Un>0 " n.

 расходится => In-неограниченная возрастающая последовательность.
расходится => In-неограниченная возрастающая последовательность. , где х0- центр ряда, а0,а1,…- коэффициенты степенного ряда, называется степенным рядом.
, где х0- центр ряда, а0,а1,…- коэффициенты степенного ряда, называется степенным рядом.
 некоторое число
некоторое число 
 , то графиком является параболоид вращения
, то графиком является параболоид вращения 

 D функция x=x(t) и y=y(t) – дифференцируемые функции независимой переменной t, то производная сложной функции z(t)=ƒ(x(t);y(t)) вычисляется по формуле
D функция x=x(t) и y=y(t) – дифференцируемые функции независимой переменной t, то производная сложной функции z(t)=ƒ(x(t);y(t)) вычисляется по формуле (1)
(1) или
или 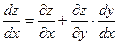 (2)
(2) и
и  можно найти, используя формулу (1) следующим образом. Зафиксировав v, заменяем в ней
можно найти, используя формулу (1) следующим образом. Зафиксировав v, заменяем в ней  ,
,  ,
,  соответствующими частными производными
соответствующими частными производными 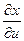 ,
,  :
: (3)
(3)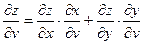
 (α≠0, α≠1) (1)
(α≠0, α≠1) (1) (1′)
(1′) , уравнение приводится к линейному
, уравнение приводится к линейному  (2)
(2)


