
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Радиус, интервал сходимости степенного ряда. Способы нахождения радиуса сходимости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. Если ряд Док-во: Обозначим через Х множество точек х, в которых Возьмем теперь любое х, для которого |x|<R. Согласно свойству точной верхней грани найдется х0ÎХ такое, что |x|<|x0|£R, откуда по теореме Абеля следует абсолютная сходимость ряда при взятом х. Возьмем теперь любое х, для которого |x|>R. Такое хÏХ. Следовательно, при этом х ряд расходится. Интервал (-R;R) называется интервалом сходимости. Число R называется интервалом сходимости. Если х0- центр степенного ряда, то интервалом сходимости будет являться промежуток (х0-R;х0+R). Если интервал сходимости охватывает всю числовую прямую, то пишут R=¥, если вырождается в одну точку, то пишут R=0.
Теорема о равномерной сходимости степенного ряда, следствия из нее. Теорема. Степенной ряд a0+a1x+a2x2+… сходится равномерно на любом отрезке [-b;b], полностью лежащем внутри интервала сходимости. Док-во: Выберем х0 b<x0<R => в точке х0 ряд сходится абсолютно => |a0|+|a1x0|+|a2x02|+… Для любого х принадлежащего промежутку [-b;b] |x|<|x0|;
Ряд Тейлора. Достаточные условия разложимости функции в ряд Тейлора. Ряд Тейлора:
Теорема. Если функция f(x) в интервале (x0-R, x0+R) дифференцируема любое число раз и все производные ограничены одним и тем же числом М: |f(n)(x)|£M для любого х, то функция разложима на этом интервале в ряд Тейлора.
Ряд Маклорена для некоторых элементарных функций. Ряд Маклорена для функции f(x):
1. f(x)=ex f’(x)=f”(x)=…=f(n)(x)=ex при х=0 получаем f’(0)=f”(0)=…=f(n)(0)=1 => ряд Маклорена для функции ex:
2. f(x)=sin(x) f’(x)=cos(x)=sin(x+ при х=0 получаем f(0)=0, f’(0)=1, f”(0)=0, f’’’(0)=-1, f(4)(0)=0 => ряд Маклорена для функции sin(x):
3. f(x)=cos(x) Почленно дифференцируем ряд для sin(x)
Приложения степенных рядов. Ряд вида
Степенные ряды с комплексными членами. Круг сходимости.
|z-z0|<R Окружность радиусом R, где R – радиус сходимости, называется кругом сходимости.
44. Скалярное произведение в пространстве C[a,b] – множество всех функций, непрерывных на отрезке [a;b]. Скалярное произведение:
Тригонометрический ряд Фурье. Вывод формул для коэффициентов Фурье. Теорема Дирихле. Тригонометрический ряд Фурье:
a0,a1,b1,a2,b2,…,an,bn,… – коэффициенты тригонометрического ряда.
Теорема Дирихле. Если f(x) – кусочногладкая функция, определенная (-p;p), то ее ряд Фурье сходится к функции f(x) во всех точках, где она непрерывна. В точке разрыва функции f(x) сумма ряда равна Функция называется гладкой на интервале (a,b) если f и f’ непрерывна (a,b). Замечание: Если f(-p)=f(p) и f(x)-гладкая на (-p;p), то сумма ряда Фурье – непрерывная ф-ия на (-¥;¥).
46. Разложение в ряд Фурье четных и нечетных функций. Разложение в ряд Фурье на отрезке 1. Если f(x) – четная, определенная на (-p;p) f(x)*sin nx – нечетная, bn=0; f(x)*cos nx – четная,
2. Если f(x) – нечетная
f(x)*cos nx – нечетная, аn=0; f(x)*sin nx – четная,
Пусть f(x) заданы на (-l;l)
Функции многих переменных 47. Понятие функции многих переменных, область определения, график (n =2). Функцией 2-х переменных, определенной на мн-ве DcR2, называется закон сопоставляющий каждой точке с координатами Множество совокупностей значение переменной называют областью определения ф-ции. Геометрической интерпретацией функции двух переменных f(x,y) служит поверхность z=f(x,y), которую называют графиком этой функции. Например, если
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.49.213 (0.006 с.) |

 сходится не при всех значениях х и не только при х=0, то существует число R>0 такое, что ряд абсолютно сходится при |х|<R и расходится при |x|>R.
сходится не при всех значениях х и не только при х=0, то существует число R>0 такое, что ряд абсолютно сходится при |х|<R и расходится при |x|>R. . Так как ряд сходится не только при х=0, то R>0.
. Так как ряд сходится не только при х=0, то R>0.

 - элементы сходящегося числового ряда => ряд мажорируем в [-b;b].
- элементы сходящегося числового ряда => ряд мажорируем в [-b;b].


 => ряд сходится.
=> ряд сходится.

 ), f”(x)=-sinx=sin(
), f”(x)=-sinx=sin( ),…, f(n)(x)=sin(
),…, f(n)(x)=sin( )/
)/
 откуда
откуда
 , где х0- центр ряда, а0,а1,…- коэффициенты степенного ряда, называется степенным рядом.
, где х0- центр ряда, а0,а1,…- коэффициенты степенного ряда, называется степенным рядом. Ряд вида
Ряд вида 
 , где z - комплекснаяпеременная, an и z0 – комплексные числа, называется степенным рядом с комплексными переменными.
, где z - комплекснаяпеременная, an и z0 – комплексные числа, называется степенным рядом с комплексными переменными. . Ортогональная система функций. Доказательство ортогональности тригонометрической системы функций
. Ортогональная система функций. Доказательство ортогональности тригонометрической системы функций  на
на  .
.












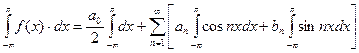





 , в точке ±p сумма ряда равна
, в точке ±p сумма ряда равна  .
. .
. ;
;










 некоторое число
некоторое число 
 , то графиком является параболоид вращения
, то графиком является параболоид вращения 




