
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные признаки сходимости знакоположительных рядовСодержание книги Поиск на нашем сайте
Первый признак сравнения. Если даны два ряда Второй (предельный) признак сравнения. Если даны два ряда В качестве эталонного ряда часто берут ряд Дирихле Пример 4.2. Исследовать на сходимость следующий числовой ряд:
Решение. Рассмотрим ряд, полученный из старших членов числителя и знаменателя
Поскольку эталонный ряд расходится, то и сравниваемый ряд также расходится. Признак Даламбера. Пусть дан ряд Отметим, что, как правило, признак Даламбера применяется для рядов, содержащих факториалы. Факториалом называется выражение Пример 4.3. Исследовать на сходимость следующий числовой ряд:
Решение. Применим к данному ряду признак Даламбера. Поскольку
Таким образом, исходный ряд является сходящимся. Радикальный признак Коши. Пусть дан ряд Пример 4.4. Исследовать на сходимость следующий числовой ряд:
Решение. Применим к данному ряду признак Коши. Используя второй замечательный предел, получим
Следовательно, исходный ряд является сходящимся. Признак Лейбница сходимости знакопеременных рядов. Если члены знакочередующегося ряда Пример 4.5. Исследовать на сходимость числовой ряд:
Решение. Применим признак Лейбница. Для данного ряда
и выполняется условие Отметим, что соответствующий знакоположительный ряд
является расходящимся (его можно сравнить с расходящимся гармоническим рядом Степенные ряды Степенным рядом называется следующее выражение
Областью сходимости степенного ряда называется такие значения x, при которых получающиеся числовые ряды будут сходящимися. Для степенного ряда область сходимости будет иметь следующий вид
где R – радиус сходимости степенного ряда, который можно найти по одной из формул:
Пример 4.6. Найти радиус и интервал сходимости следующего степенного ряда, а также исследовать его на сходимость на концах интервала:
Решение. Найдем радиус сходимости степенного ряда:
Тогда область сходимости будет иметь вид (x 0– R, x 0+ R), т.к. в нашем случае x 0=–7, то область сходимости будет иметь вид (–16; 2). Исследуем теперь сходимость ряда на границах области сходимости, т.е. в точках
который сходится по признаку Лейбница. При x =2 получается числовой ряд
который является расходящимся, т.к. его можно сравнить с расходящимся гармоническим рядом Если функция
Пример 4.7. Разложите данную функцию f (x) в ряд Тейлора в окрестности точки x 0 (выпишете первых три ненулевых члена ряда):
Решение. Находим:
Таким образом, первых три ненулевых члена ряда Тейлора исходной функции будут иметь следующий вид
Ряд Тейлора в окрестности точки x 0=0 называется рядом Маклорена:
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.008 с.) |

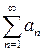 и
и 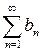 , общие члены которых удовлетворяют соотношению
, общие члены которых удовлетворяют соотношению 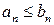 , то из сходимости второго ряда следует сходимость первого ряда и из расходимости первого ряда следует расходимость второго ряда.
, то из сходимости второго ряда следует сходимость первого ряда и из расходимости первого ряда следует расходимость второго ряда. , отличный от нуля, то оба ряда сходятся и расходятся одновременно.
, отличный от нуля, то оба ряда сходятся и расходятся одновременно. , который сходится при a>1, и расходится при a£1.
, который сходится при a>1, и расходится при a£1.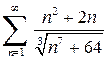
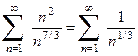 . Это будет ряд Дирихле с
. Это будет ряд Дирихле с 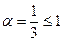 , который расходится. Применим предельный признак сравнения:
, который расходится. Применим предельный признак сравнения: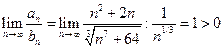 .
.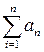 и существует предел
и существует предел 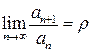 . Тогда если r>1, то ряд расходится, если r<1, то ряд сходится, если r=1, то ряд может сходиться и расходиться, т.е. требуется применить другой признак сходимости.
. Тогда если r>1, то ряд расходится, если r<1, то ряд сходится, если r=1, то ряд может сходиться и расходиться, т.е. требуется применить другой признак сходимости.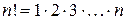 .
.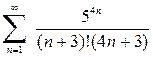
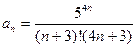 ,
, 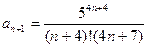 ,
,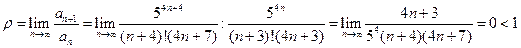 .
.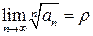 , тогда если r>1, то ряд расходится, если r<1, то ряд сходится, если r=1, то ряд может сходиться и расходиться, т.е. требуется применить другой признак сходимости.
, тогда если r>1, то ряд расходится, если r<1, то ряд сходится, если r=1, то ряд может сходиться и расходиться, т.е. требуется применить другой признак сходимости.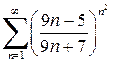 .
.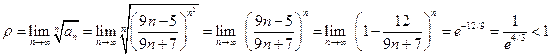 .
.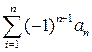 удовлетворяют условиям: 1)
удовлетворяют условиям: 1) 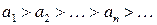 , 2)
, 2) 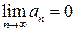 , то ряд сходится, его сумма положительна и не превосходит первого члена
, то ряд сходится, его сумма положительна и не превосходит первого члена 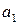 , т.е.
, т.е. 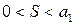 .
.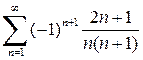 .
.
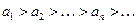 , т.к. при больших n члены ряда an ведут себя как 2/ n. Следовательно, исходный ряд является сходящимся.
, т.к. при больших n члены ряда an ведут себя как 2/ n. Следовательно, исходный ряд является сходящимся.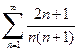
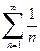 ). Такие ряды называются условно сходящимися.
). Такие ряды называются условно сходящимися.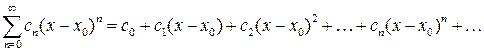 (4.2)
(4.2)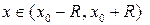 ,
,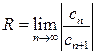 ,
, 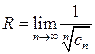 . (4.3)
. (4.3)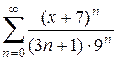 .
.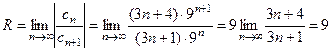 .
.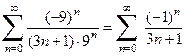 ,
,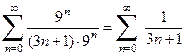 ,
,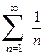 . Итак, область сходимости исходного степенного ряда будет иметь окончательно следующий вид [–16; 2).
. Итак, область сходимости исходного степенного ряда будет иметь окончательно следующий вид [–16; 2).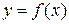 бесконечно число раз дифференцируема в окрестности точки x 0, то её можно разложить в ряд Тейлора:
бесконечно число раз дифференцируема в окрестности точки x 0, то её можно разложить в ряд Тейлора: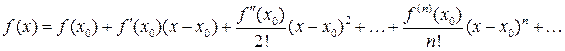 (4.4)
(4.4)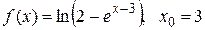 .
.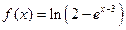 ,
,
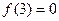 ;
;
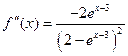 ,
,
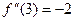 ;
;
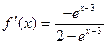 ,
,
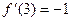 ;
;
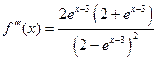 ,
,
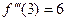 .
.
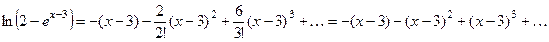
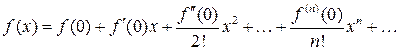 (4.5)
(4.5)


