
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема исследования графика функцииСодержание книги Поиск на нашем сайте
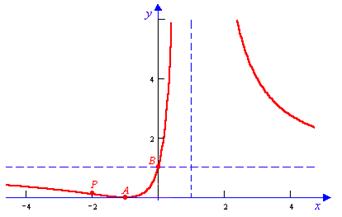
I. а) Найти область определения функции. б) Установить чётность, нечётность, периодичность функции. в) Определить точки пересечения графика функции с осями координат. г) Определить интервалы непрерывности функции и найти точки разрыва. II. Определить интервалы монотонности графика функции и найти точки экстремума. III. Определить интервалы выпуклости и вогнутости графика функции и найти точки перегиба. IV. Найти асимптоты графика функции. V. Построить график функции. Пример 2.9. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
Решение. I. а) Данная функция имеет смысл при всех значениях x, кроме точки x =1, т.е. область определения данной функции
Заметим также, что функция может принимать только неотрицательные значения, т.е. y ³0. б) Данная функция является ни четной, ни нечетной, ни периодической, т.е. это функция общего вида. в) При x =–1 функция будет равна нулю: y (–1)=0, т.е. график функции пересекает ось Ox в точке A (–1;0). При x =0 функция принимает значение y (0)=1, т.е. график функции пересекает ось Oy в точке B (0; 1). г) Точка x =1 является точкой разрыва 2-го рода, причем
Следовательно, прямая x =1 является вертикальной асимптотой данной функции. II. Исследуем функцию на экстремум и определим участки ее монотонности. Для этого вычислим производную:
III. Исследуем функцию на выпуклость и вогнутость. Для этого вычислим производную второго порядка:
IV. Найдем уравнение наклонной асимптоты y=kx+b, где
Таким образом, рассматриваемая функция имеет горизонтальную асимптоту, уравнение которой y =1. V. Строим график функции. Построение начинаем с изображения асимптот, а также наносим точки экстремума, точки перегиба и точки пересечения с осями координат (см. рис.).
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Неопределенные интегралы Понятие интеграла, наряду с производной, является одним из основных в математическом анализе. Он играет большую роль в приложениях. Поэтому стоит более глубоко ознакомится с этим понятием по приведенной литературе. Функция F (x) называется первообразной функции f (x) на (a, b), если Совокупность всех первообразных
В этом равенстве f (x) называется подынтегральной функцией, а f (x) dx – подынтегральным выражением. Свойства неопределенных интегралов
Таблица простейших интегралов
Пример 3.1. Вычислить неопределенные интегралы:
Решение. а) Используя свойства 3 и 4, получим
Далее, используя из таблицы интегралов формулы 2 и 4, находим
Тогда
б) Используя свойство 5 и формулу 5, получим
в) Здесь используем формулу 3 с учётом свойства 5:
г) Запишем подынтегральную функцию следующим образом:
Тогда, с чётом формулы 12 и свойства 5, получаем
Метод замены переменной. Положим x =j(t), где j(t) – дифференцируемая функция. Учтём, что дифференциал вычисляется по формуле
Тогда справедлива следующая формула
Пример 3.2. Вычислить неопределенные интегралы, используя метод замены переменной:
а) Решение. а) При вычислении первого интеграла сделаем подстановку t =5–9ln x, в результате получим
б) При вычислении второго интеграла сделаем подстановку t =5+4 x 10, в результате получим
Метод интегрирования по частям. Если u (x) и v (x) – дифференцируемые функции, то справедлива формула
Данную формулу интегрирования применяют обычно в тех случаях, когда функция u (x) упрощается при дифференцировании, а первообразная для функции v (x) легко находится. Пример 3.3. Вычислить неопределенные интегралы, используя метод замены переменной: а) Решение. а) При вычислении первого интеграла воспользуемся формулой интегрирования по частям:
б) При вычислении второго интеграла также воспользуемся формулой интегрирования по частям. В результате получим
Дробно-рациональной функцией (или рациональной дробью) называется выражение
Если n ³ m, дробь называется неправильной. Если n < m, дробь называется правильной. Любую неправильную рациональную дробь можно представить в виде суммы целой части (т.е. многочлена) и правильной дроби. Пример 3.4. Вычислить интеграл:
Решение. Выделим целую и дробную части рациональной дроби, для этого разделим столбиком два многочлена (числитель на знаменатель):
В результате получаем
Любую правильную рациональную дробь можно представить в виде суммы простейших дробей вида:
Чтобы правильную рациональную дробь представить в виде суммы простейших дробей, нужно сначала знаменатель разложить линейные и квадратичные множители вида (x+a) и Пример 3.5. Вычислить интеграл:
Решение. Разложим подынтегральную функцию, т.е. правильную рациональную дробь, на сумму простейших дробей:
Приведем правую часть равенства к общему знаменателю и приравняем числители левой и правой частей:
Чтобы найти неопределенные коэффициенты A, B, C, придадим переменной x три каких-либо значения (обычно выбирают такие значения, чтобы получались нулевые значения в правой части):
Таким образом,
Далее вычисляем исходный интеграл как сумму интегралов от простейших дробей:
При вычислении интегралов вида
следует преобразовать подынтегральную функцию, используя различные тригонометрические формулы. Если хотя бы одно из чисел m или n – нечётное положительное, то применяют подстановку cos x = t, если n – нечётное и sin x=t, если m – нечётное. При этом используется основное тригонометрическое тождество:
Пример 3.6. Вычислить интеграл:
Решение. Применяем подстановку sin x=t, cos xdx=dt:
Если m или n – чётные положительные числа, то применяются тригонометрические формулы понижения степени:
Пример 3.7. Вычислить интеграл:
Решение. Преобразуем подынтегральное выражение следующим образом
Если m + n – чётное отрицательное число, то применяют подстановку Пример 3.8. Вычислить интеграл:
Решение. Преобразуем подынтегральное выражение следующим образом
При вычислении интегралов вида
следует преобразовать подынтегральную функцию, используя следующие тригонометрические формулы:
Пример 3.9. Вычислить интеграл:
Решение. Преобразуем подынтегральное выражение следующим образом
Определенные интегралы Пусть функция f (x) определена на отрезке [ a,b ]. Этот отрезок разделим на n произвольных, необязательно равных, частей: a=x 0 < x 1 <... < xn=b. В этом случае говорят, что произведено разбиение отрезка [ a,b ]. На каждом участке разбиения [ xi –1, xi ] возьмем произвольную точку ci и вычислим значение функции f (x) в этих точках. Если умножить полученные значения функции f (ci) на длину соответствующего участка D xi = xi – xi –1 и просуммировать все эти выражения, то получим сумму
которая называется интегральной суммой функции f (x) на отрезке [ a,b ]. Обозначим через D x =max D xi. Определение. Если предел последовательности интегральных сумм
существует, т.е. конечен и не зависит от способа разбиения отрезка [ a,b ] и от выбора точек ci на соответствующих участках, то этот предел называется определенным интегралом функции f(x) на отрезке [ a,b ] и обозначается
Здесь число a называется нижним пределом, число b называется верхним пределом интеграла. Функция f (x) называется интегрируемой на отрезке [ a,b ], если для этой функции на указанном отрезке существует предел интегральных сумм, т.е. определенный интеграл. Необходимое условие интегрируемости: если функция f (x) интегрируема на отрезке [ a,b ], то она ограничена на этом отрезке. Достаточное условие интегрируемости: если функция f (x) непрерывна на отрезке [ a,b ], или имеет конечное число точек разрыва 1-го рода, то она интегрируема на этом отрезке.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.207.176 (0.008 с.) |

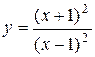 .
.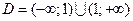 .
.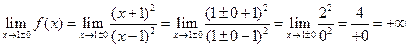 .
.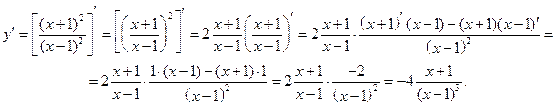
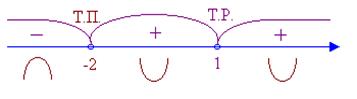
 Определим критические точки функции, т.е. точки в которых производная равна нулю или не существует. Это будут точки x 1=–1, x 2=1. Наносим эти точки на числовую ось и определяем знак производной на каждом из полученных интервалов. Поскольку при переходе через критическую точку x =–1 производная меняет знак с минуса на плюс, то в этой точке имеется минимум: y(–1)=0. В точке x =1 производная также меняет знак, однако в этой точке нет экстремума, т.к. эта точка является точкой разрыва. На интервалах (–¥; –1) и (1;+¥) функция убывает, на интервале (–1; 1) – возрастает.
Определим критические точки функции, т.е. точки в которых производная равна нулю или не существует. Это будут точки x 1=–1, x 2=1. Наносим эти точки на числовую ось и определяем знак производной на каждом из полученных интервалов. Поскольку при переходе через критическую точку x =–1 производная меняет знак с минуса на плюс, то в этой точке имеется минимум: y(–1)=0. В точке x =1 производная также меняет знак, однако в этой точке нет экстремума, т.к. эта точка является точкой разрыва. На интервалах (–¥; –1) и (1;+¥) функция убывает, на интервале (–1; 1) – возрастает.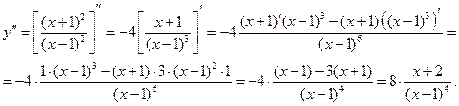
 Определим критические точки 2-го порядка, т.е. точки в которых вторая производная равна нулю или не существует. Это будут точки x 1=–2, x 2=1. Нанесем эти точки на числовую ось и определим знак второй производной на каждом из полученных интервалов. Поскольку при переходе через критическую точку
Определим критические точки 2-го порядка, т.е. точки в которых вторая производная равна нулю или не существует. Это будут точки x 1=–2, x 2=1. Нанесем эти точки на числовую ось и определим знак второй производной на каждом из полученных интервалов. Поскольку при переходе через критическую точку 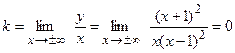 ,
, 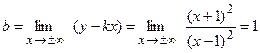 .
.
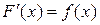 для любого
для любого 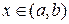 . Если F 1(x) и F 2(x) две первообразные функции f (x), то
. Если F 1(x) и F 2(x) две первообразные функции f (x), то 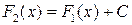 , т.е. любые две первообразные одной и той же функции отличаются друг от друга на постоянную величину.
, т.е. любые две первообразные одной и той же функции отличаются друг от друга на постоянную величину.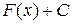 функции f (x) называется неопределенным интегралом от функции f (x) и обозначается символом
функции f (x) называется неопределенным интегралом от функции f (x) и обозначается символом  , т.е.
, т.е. . (3.1)
. (3.1)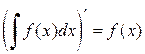 ,
,
 ,
,
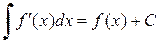 ,
,
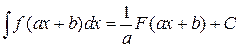 .
.
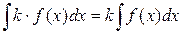 ,
,
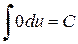 ,
,
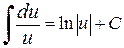 ,
,
 , a ¹1,
, a ¹1,
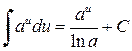 ,
,
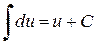 ,
,
 ,
,
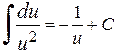 ,
,
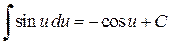 ,
,
 ,
,
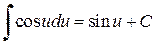 ,
,
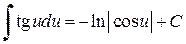 ,
,
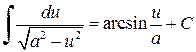 ,
,
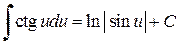 ,
,
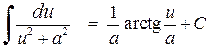 ,
,
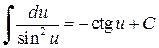 ,
,
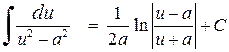 ,
,
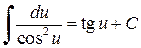 ,
,
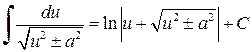 .
.
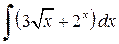 ,
,
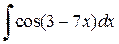 ,
,
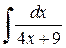 ,
,
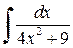 .
.
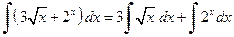 .
.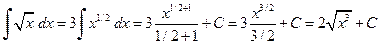 ,
, 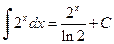 .
.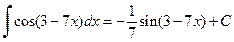 .
.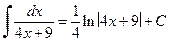 .
.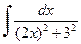 .
.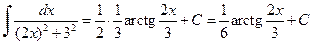 .
.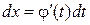 .
.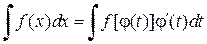 . (3.2)
. (3.2)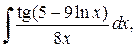 б)
б)  .
.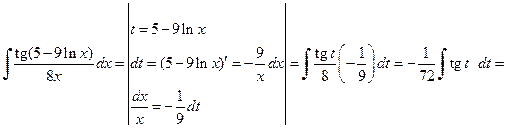
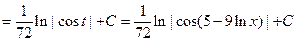 .
.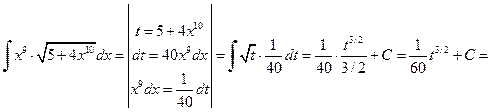
 .
.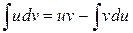 . (3.3)
. (3.3) б)
б) 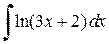 .
.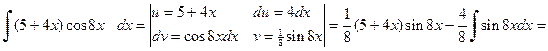
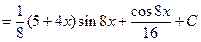 .
.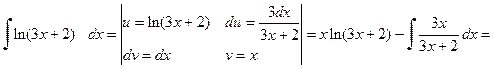
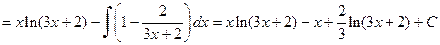 .
.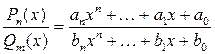 .
.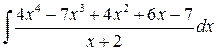 .
.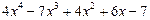
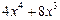
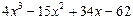


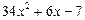
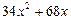
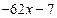
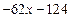
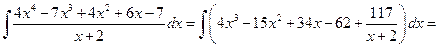
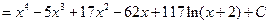 .
. ,
,
 ,
,
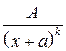 ,
,
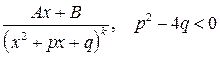 .
.
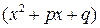 . В зависимости от полученных множителей получается соответствующее разложение на сумму простейших дробей. Рассмотрим этот метод на конкретном примере.
. В зависимости от полученных множителей получается соответствующее разложение на сумму простейших дробей. Рассмотрим этот метод на конкретном примере.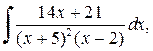 .
. .
.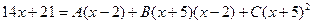 .
.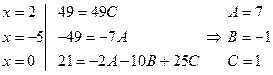
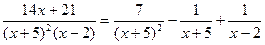 .
.
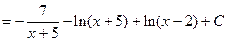 .
.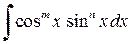 ,
, . (3.4)
. (3.4)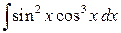 .
.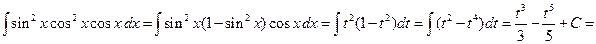
 .
.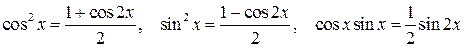 . (3.5)
. (3.5)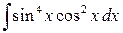 .
.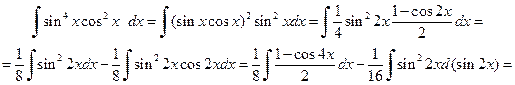
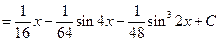 .
.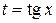 или
или 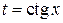 .
.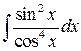 .
.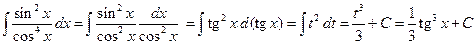 .
. ,
, 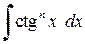
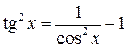 ,
, 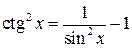 . (3.6)
. (3.6)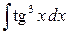 .
.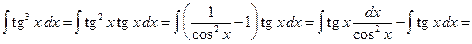
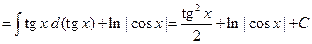 .
.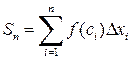 , (3.7)
, (3.7) . (3.8)
. (3.8) . (3.9)
. (3.9)


