
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства бесконечно-малых и бесконечно-больших величинСодержание книги Поиск на нашем сайте
Пусть C ¹0 и a, b и g – бесконечно-малые величины, то 1. 2.. a+b=g, ¥+¥=¥, ¥± C =¥; 3. a×b=g, a× C =b или 0× C =0, ¥×¥=¥, ¥× C =¥. Свойства пределов 1. 2. 3. 4. 5. 6. При вычислении пределов
2) Функция f (x) не определена в предельной точке a. В этом случае мы будем иметь дело с т.н. неопределенностями: Раскрытие неопределенностей вида Пример 1.2. Вычислить пределы: а) Решение. а) Здесь мы имеем с неопределенностью вида
б) Здесь мы имеем с неопределенностью вида ¥–¥. Умножим и разделим данное выражение на точно такое же, но со знаком плюс между слагаемыми (на сопряженное выражение):
В результате получилась неопределенность типа
Раскрытие неопределенностей вида
Пример 1.3. Вычислить пределы: а) Решение. а) Здесь мы имеем с неопределенностью вида
б) Здесь мы имеем с неопределенностью вида
Первый замечательный предел:
Из этого предела также вытекает
Второй замечательный предел:
Второй замечательный предел имеет место при неопределенности вида 1¥. Его также записывают в виде
Из второго замечательно предела вытекает
При вычислении пределов вида
В этом случае пишут a(x)~b(x). Тогда в вычислениях пределов вместо одной бесконечно-малой величины можно брать другую эквивалентную бесконечно-малую величину. Таблица эквивалентностей Пусть a(x) – бесконечно-малая величина в окрестности точки x 0. Тогда
Пример 1.4. Вычислить пределы:
Решение. Используя метод эквивалентных бесконечно-малых величин, получаем
При использовании второго замечательного предела воспользуемся следующим равенством:
где f (x)®0, g (x)®¥ при x ® x 0. Пример 1.5. Вычислить пределы: а) Решение. а) Здесь мы имеем с неопределенностью вида
Далее, используя равенство (1.1), получим
б) Здесь мы также имеем с неопределенностью вида
Учитывая (1.1), где
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.006 с.) |

 ,
,  ;
; ,
,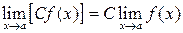 ,
,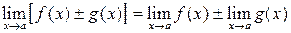 ,
,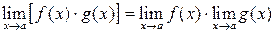 ,
,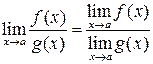 , если
, если 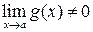 ,
,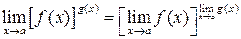 .
.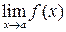 встречаются два случая.1) Функция f (x) определена в предельной точке a, тогда
встречаются два случая.1) Функция f (x) определена в предельной точке a, тогда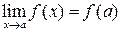 .
.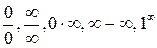 и т.п. Раскрытие (устранение) неопределенностей составляется основное содержание предлагаемых задач.
и т.п. Раскрытие (устранение) неопределенностей составляется основное содержание предлагаемых задач.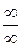 . Рассмотрим пределы вида
. Рассмотрим пределы вида  , где P (x) и Q (x) – многочлены. В этом случае можно воспользоваться следующей теоремой: сумма конечного числа бесконечно больших функций различных порядков эквивалентна слагаемому высшего порядка.
, где P (x) и Q (x) – многочлены. В этом случае можно воспользоваться следующей теоремой: сумма конечного числа бесконечно больших функций различных порядков эквивалентна слагаемому высшего порядка.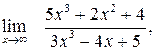 б)
б) 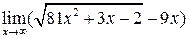 .
.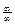 . Тогда используя последнюю теорему, получим
. Тогда используя последнюю теорему, получим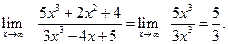
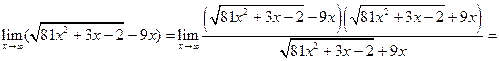
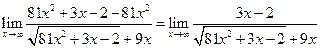 .
. .
.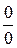 . Рассмотрим пределы вида
. Рассмотрим пределы вида 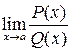 , где P (x) и Q (x) – многочлены. В этом случае числитель и знаменатель можно разложить на множители
, где P (x) и Q (x) – многочлены. В этом случае числитель и знаменатель можно разложить на множители .
. б)
б)  .
.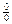 . Разложим данное выражение на множители, а затем сократим дробь на x –1¹0 (x ®1, но x ¹1):
. Разложим данное выражение на множители, а затем сократим дробь на x –1¹0 (x ®1, но x ¹1):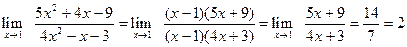 .
.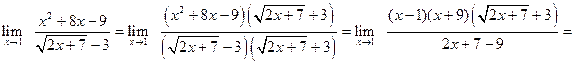
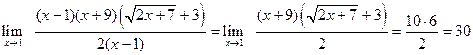 .
.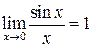 . (1.1)
. (1.1) ,
, 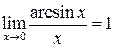 ,
, 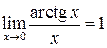 . (1.2)
. (1.2)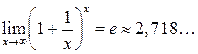 . (1.3)
. (1.3)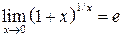 . (1.4)
. (1.4)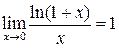 ,
, 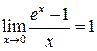 . (1.5)
. (1.5)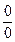 можно использовать метод эквивалентных бесконечно малых величин. Две бесконечно малые величины a(x) и b(x) называются эквивалентными в окрестности точки x 0, если
можно использовать метод эквивалентных бесконечно малых величин. Две бесконечно малые величины a(x) и b(x) называются эквивалентными в окрестности точки x 0, если .
.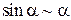 ,
,
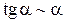 ,
,
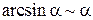 ,
,
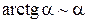 ,
,
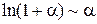 ,
,
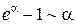 .
.
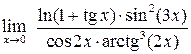 .
.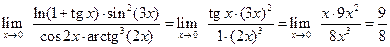 .
.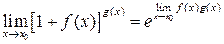 , (1.6)
, (1.6) б)
б) 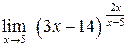 .
.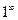 . Преобразуем выражение в скобках
. Преобразуем выражение в скобках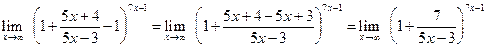 .
.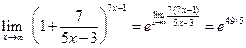 .
.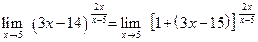 .
.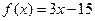 и
и 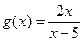 , получим
, получим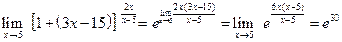 .
.


