
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные функции одной переменнойСодержание книги Поиск на нашем сайте Понятие производной является одной из основным математическом анализе, играющим большую роль и в экономических исследованиях. Поэтому стоит более глубоко ознакомится с этим понятием, например, по литературе, приведенной в конце методических указаний. Производной функции y = f (x) в точке x 0 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится нулю:
Производная функции имеет несколько обозначений: Основные правила дифференцирования
Таблица производных простейших элементарных функций
Пример 2.1. Найти производные dy / dx данных функций: а) Решение. а) При вычислении производной данной функции воспользуемся формулой (ua) ' = aua –1 u'. Тогда производная исходной функции найдется следующим образом:
б) В данном случае воспользуемся правилом дифференцирования частного:
в) Используя правило дифференцирования сложной функции, получим
При вычислении производной сложно-показательной функции Пример 2.2. Найти производную:
Решение. При вычислении производной данной функции, прологарифмируем исходное выражение:
Теперь продифференцируем полученное выражение, учитывая, что y является функцией от x:
Отсюда
Если y как функция от x задаётся посредством уравнения
то y называется функцией от x, заданной неявно. Производная от такой функции может быть найдена следующим образом. Находим производную по x от функции Пример 2.3. Найти производную функции, заданной неявно:
Решение. При вычислении производной от неявно заданной функции следует продифференцировать исходное уравнение по x с учетом того, что переменная y зависит от x: y=y (x) и
Сгруппируем слагаемые, содержащие y':
Отсюда находим
Пусть зависимость между x и y задана параметрически в виде двух уравнений
где t – вспомогательная переменная, называемая параметром. Производная от такой функции может быть найдена по формуле:
Пример 2.4. Найти производную функции, заданной параметрически:
Решение. Находим производные от функций x (t) и y (t):
Тогда
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 . (2.1)
. (2.1) ,
,  ,
,  . Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например,
. Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например,  . Операция нахождения производной функции называется дифференцированием.
. Операция нахождения производной функции называется дифференцированием. ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
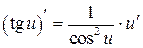 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
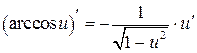 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 ,
,
 , б)
, б) 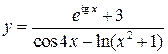 ,
, .
.

 .
. . В результате получим
. В результате получим
 .
. .
. следует функцию предварительно прологарифмировать, а затем уже искать производную. Такой приём называется логарифмическим дифференцированием.
следует функцию предварительно прологарифмировать, а затем уже искать производную. Такой приём называется логарифмическим дифференцированием. .
. .
.
 .
. , (2.2)
, (2.2) , учитывая при этом y=y (x) как функцию от x, и приравниваем её к нулю. Разрешаем полученное уравнение относительно y ¢; в результате будем иметь выражение производной от неявной функции в виде: y ¢= f (x,y).
, учитывая при этом y=y (x) как функцию от x, и приравниваем её к нулю. Разрешаем полученное уравнение относительно y ¢; в результате будем иметь выражение производной от неявной функции в виде: y ¢= f (x,y).
 :
: .
. .
. .
. , (2.3)
, (2.3) . (2.4)
. (2.4)
 .
. .
.


