
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимый признак сходимости.Содержание книги
Поиск на нашем сайте
Необходимый признак сходимости. Если числовой ряд Следствие Если Ряд вида Числовой ряд вида
Интегральный признак Коши Пусть члены ряда Тогда несобственный интеграл Ряд Дирихле – ряд вида Ряд сх-ся при p> 1 и расх-ся при p
2. Первый признак сравнения Пусть имеется два ряда с положительными членами:
Если члены ряда (А) не больше соответствующих членов ряда (В) Если члены ряда (А) не меньше соответствующих членов ряда (В) Второй признак сравнения Пусть имеются два ряда с положительными членами Если предел отношения их n -ых членов
3. Признак сходимости Даламбера Если у числового ряда с положительными членами 1. ряд сходится, если q<1, 2. расходится, если q>1, 3. q=1 данный признак не дает ответа на вопрос о сходимости ряда. Нужно использовать др. признаки кроме радикального Коши Радикальный признак Коши Если у числового ряда с положит. членами 1. ряд сходится, если q<1, 2. расходится, если q>1, 3. q=1 данный признак не дает ответа на вопрос о сходимости ряда. Нужно использовать др. признаки кроме признака Даламбера.
Признак Лейбница Если члены знакочередующегося ряда 1) an>an+1 > an+2>… (не возрастают) 2) а) заданный ряд сходится условно; б) его сумма не превосходит первого члена.
8. Степенным наз. функцион. ряд вида Числа Теорема Абеля Если степенной ряд сх-ся в точке x0
Из теоремы Абеля следует, что существует такое число R > 0, называемое радиусом сходимости, что степенной ряд сх-ся (абсолютно) для любых x, таких что 9. Рядом Тейлора называют ряд: (1) Если в разложении ф-и в ряд Тейлора (2) взять a=0, то получим частный случай ряда Тейлора, называемый рядом Маклорена:
7. Ряд называется знакопеременным, если среди его членов есть как положительные, так и отрицательные. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов. Знакопеременный ряд называется условно сходящимся, если сам ряд с сходится, а ряд, составленный из модулей – расходится.
Числовой ряд наз. знакочередующимся, если любые два его соседние члены имеют разные знаки:
Пусть задана бесконечная послед-ность ф-й { un(x) }. Функциональный ряд -сумма всех ее членов: u1(x)+u2(x)+…+un(x)+…=
Геометрическая вероятность Пусть имеется пространство событий, элементарные исходы которого можно представить в виде точек, заполняющих нек. область Ω в пространстве R 3. Если при этом событию А благоприятствуют элемен-тарные события, заполняющие нек. подоб-ласть D из Ω, то геометр. вероятностью события А наз. отношение объема области D к объему области Ω: Аналогично определяется геометр. вероят-ность события, когда множ-во Ω представ-ляет собой нек. область на плоскости или отрезок на прямой линии. В этих случаях объемы областей заменяются, соответст-но, площадями фигур или длинами отрезков. Случайное событие – событие, которое может произойти (не произойти), если будет выполнена определённая совок-сть условий S, которая наз. испытанием. Несколько событий наз совместными, если в результате испытания появление 1-го из них не исключает появления другого в одном и том же испытании.
Несколько событий наз несовместными, если в результате испытания появ-ление 1-го из них исключает появление других (остальных) событий в одном и том же испытании (выпадение очков на игральной кости – 6 несовмес. событий).
2 события наз. равновозможными, если нет оснований считать, что появление одного из них более возможно, чем появление другого. (выбрасывание орла и решки - равновозможные события). Полная группа событий – совок-сть случаных событий, если в результате испытания появится хотя бы 1 из них. С=
Для решения вероятностных задач используют формулы комбинаторики: 1) число перестановок Pn из n элементов равно: Перестановки – комбинации, которые можно составить из n эл-тов по n эл-тов в каждой, чтобы они отличались только порядком расположения этих эл-тов. 2) число размещений Размещение – комбинации, которым можно составить из n эл-тов по m эл-тов в каждой и отличающихся друг от друга либо составом эл-тов, либо порядком расположения эл-тов. 3) число различных сочетаний Сочетания – комбинации, которые можно составить из n эл-тов по m эл-тов в каждой и отличающихся друг от друга только составом эл-тов. Правило суммы Если объект А может быть извлечён из нек. совок-сти объектов m способами, а объект В может быть извлечён из совок-сти объектов n способами, то извлечь объект А и объект В (либо А, либо В) можно n+m способами Правило произведения Если объект А может быть извлечён из нек. совок-сти объектов m способами и для каждого способа извлечения объекта А объект В может быть извлечён n способами, то извлечь объект А, и объект В можно nm способами.
Суммой событий А и В наз. событие С = А + В, состоящее в наступлении хотя бы 1-го из этих событий. Если А и В – несовместные, то А+В – это событие, состоящее в наступлении либо события А, либо события В.
Если А и В – совместные, то А+В – это события, состоящие в наступлении либо события А, либо события В, либо события АВ (и А, и В).
Биномиальное распределение Пусть имеются n испытаний, в каждом из которых событие А может появиться с вероятностью р (0<p<1) или не появиться с вероятностью q (q=1-p). Рассмотрим дискретную СВ Х – число появлений события А в испытаниях. Её возможные значения 0, 1, 2, …, n Закон Пуассона Говорят, что дискретная СВ Х распределена по закону Пуассона, если n – велико, а р – мало.
Поток событий – послед-ность событий, наступивших в случайные моменты времени. Напр., поступле-ние вызовов в скорую, на АТС, прибытие самолётов в аэропорты. Свойства потока: 1) cв-во стационарности: вероят-ность наступления события k раз за промежуток времени t зависит лишь от k и t 2) cв-во ординарности: появление 2-ух и более событий за малый про-межуток времени почти невозможно
3) отсутствие последствий: вероят-ность появления событий k раз за промежуток времени t не зависит от того, появлялись или не появлялись события в предшествующие дан-ному промежутку времени моменты Простейшим (пуассоновским) наз. поток событий, обладающий этими 3-мя свойствами. Также для потока характерно такое понятие, как интенсивность (
Необходимый признак сходимости. Если числовой ряд Следствие Если Ряд вида Числовой ряд вида
Интегральный признак Коши Пусть члены ряда Тогда несобственный интеграл Ряд Дирихле – ряд вида Ряд сх-ся при p> 1 и расх-ся при p
2. Первый признак сравнения Пусть имеется два ряда с положительными членами:
Если члены ряда (А) не больше соответствующих членов ряда (В) Если члены ряда (А) не меньше соответствующих членов ряда (В) Второй признак сравнения Пусть имеются два ряда с положительными членами Если предел отношения их n -ых членов
3. Признак сходимости Даламбера Если у числового ряда с положительными членами 1. ряд сходится, если q<1, 2. расходится, если q>1, 3. q=1 данный признак не дает ответа на вопрос о сходимости ряда. Нужно использовать др. признаки кроме радикального Коши Радикальный признак Коши Если у числового ряда с положит. членами 1. ряд сходится, если q<1, 2. расходится, если q>1, 3. q=1 данный признак не дает ответа на вопрос о сходимости ряда. Нужно использовать др. признаки кроме признака Даламбера.
Признак Лейбница Если члены знакочередующегося ряда 1) an>an+1 > an+2>… (не возрастают) 2) а) заданный ряд сходится условно; б) его сумма не превосходит первого члена.
8. Степенным наз. функцион. ряд вида Числа Теорема Абеля Если степенной ряд сх-ся в точке x0 Из теоремы Абеля следует, что существует такое число R > 0, называемое радиусом сходимости, что степенной ряд сх-ся (абсолютно) для любых x, таких что 9. Рядом Тейлора называют ряд: (1) Если в разложении ф-и в ряд Тейлора (2) взять a=0, то получим частный случай ряда Тейлора, называемый рядом Маклорена:
7. Ряд называется знакопеременным, если среди его членов есть как положительные, так и отрицательные. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов. Знакопеременный ряд называется условно сходящимся, если сам ряд с сходится, а ряд, составленный из модулей – расходится.
Числовой ряд наз. знакочередующимся, если любые два его соседние члены имеют разные знаки:
Пусть задана бесконечная послед-ность ф-й { un(x) }. Функциональный ряд -сумма всех ее членов: u1(x)+u2(x)+…+un(x)+…=
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.142.90 (0.008 с.) |

 сх-ся, то
сх-ся, то  . Обратное неверно.
. Обратное неверно.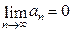 ,то
,то  расх-ся.
расх-ся. наз. гармоническим и он расх-ся.
наз. гармоническим и он расх-ся. представляет собой г еометр. прогрессию. Данный числовой ряд
представляет собой г еометр. прогрессию. Данный числовой ряд  сх-ся при
сх-ся при  и расх-ся, когда
и расх-ся, когда  .
. 
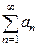 положител. и не возрастают. Рассмотрим непрерыв. убывающую ф-ю f(x), такую что f(n)=an.
положител. и не возрастают. Рассмотрим непрерыв. убывающую ф-ю f(x), такую что f(n)=an.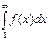 и числ. ряд
и числ. ряд 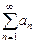 ведут себя одинаково: либо одновременно сх-ся, либо одновременно расходятся.
ведут себя одинаково: либо одновременно сх-ся, либо одновременно расходятся.
 1.
1.
 ,
,  1, то из сходимости ряда (В) следует сходимость ряда (А).
1, то из сходимости ряда (В) следует сходимость ряда (А).
 и
и  .
.
 и конечен, то ряды ведут себя одинаково: либо одновременно сх-ся, либо одновременно расх-ся.
и конечен, то ряды ведут себя одинаково: либо одновременно сх-ся, либо одновременно расх-ся. сущ-ет предел отношения последующего члена ряда к предыдущему
сущ-ет предел отношения последующего члена ряда к предыдущему 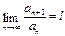 , то
, то существует
существует  , то:
, то: , an
, an 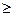 0 для
0 для 
 ,то:
,то: cnxn=c0+c1x+c2x 2 +…+cnxn.
cnxn=c0+c1x+c2x 2 +…+cnxn.  наз. коэф-ами степенного ряда. Для степ. Ряда справедлива теорема Абеля.
наз. коэф-ами степенного ряда. Для степ. Ряда справедлива теорема Абеля.  0, то он абсолютно сх-ся (абсолютно) при всех значениях x таких, что
0, то он абсолютно сх-ся (абсолютно) при всех значениях x таких, что 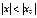 . Если степен. ряд расх-ся в некот. точке
. Если степен. ряд расх-ся в некот. точке  , то он расх-ся при всех значениях x таких, что
, то он расх-ся при всех значениях x таких, что  .
. <R., и расх-ся при любых x, таких что
<R., и расх-ся при любых x, таких что 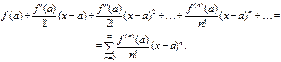 Если в области сх-сти ряд (1) сх-ся к f(x), то имеет место равенство (2)
Если в области сх-сти ряд (1) сх-ся к f(x), то имеет место равенство (2)  называемое разложением ф-и f(x) в ряд Тейлора в окрестности точки a.
называемое разложением ф-и f(x) в ряд Тейлора в окрестности точки a.

 . Точка x0 - точка сх-сти фун. р.
. Точка x0 - точка сх-сти фун. р.  , если ч.р.
, если ч.р.  явл. сх-ся. Область сх-сти функцион. ряда – совок-сть всех его точек сх-сти.
явл. сх-ся. Область сх-сти функцион. ряда – совок-сть всех его точек сх-сти.


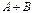 или
или  – сумма событий А и В (событие, которое заключается в том, что происходит либо событие А, либо событие В, либо события и А и В).
– сумма событий А и В (событие, которое заключается в том, что происходит либо событие А, либо событие В, либо события и А и В). или
или  – произведение собы-тий (событие, которое состоит в том, что одновременно происходят события А и В).
– произведение собы-тий (событие, которое состоит в том, что одновременно происходят события А и В). - противоположное событию А (если эти события несовместны, а их сумма – достоверное событие)-(Промах или попадание про стрельбе по мишени)
- противоположное событию А (если эти события несовместны, а их сумма – достоверное событие)-(Промах или попадание про стрельбе по мишени)
 m элементов из
m элементов из 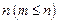 равно:
равно: 
 m элементов из n равно
m элементов из n равно 

 где k=1, 2, …, n. Это распределение наз. биномиальным с параметрами p и q.
где k=1, 2, …, n. Это распределение наз. биномиальным с параметрами p и q. где
где  =np – параметр распределения.
=np – параметр распределения. ) – среднее число появлений события за единицу времени. Вероятность того, что событие появится k раз за промежуток времени t будет равна:
) – среднее число появлений события за единицу времени. Вероятность того, что событие появится k раз за промежуток времени t будет равна:



