
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение в ряд Маклорена основных элементарных функцийСодержание книги
Поиск на нашем сайте 1. 2. Область сх-сти: 3. Область сх-сти: 4. Область сх-сти: Пусть задана периодическая ф-я f(x) с периодом T=2 На отрезке[-
коэф-ты которого определены формулами: Функц. ряд (1) наз. тригонометр. рядом Фурье для функции f(x) на отрезке [-
Ряды Фурье для четн. и нечетн. ф-й Пусть f(x) – четн. ф-я. Тогда
Разложение в ряд Фурье четной ф-и содержит только косинусы:
Пусть f(x) – нечетная функция. Тогда
Разложение в ряд Фурье нечетной ф-и содержит только синусы:
Классическое определение вероятности: вероятностью события А наз. отношение числа элементарных исходов (событий) m, благоприятствующих появлению события А, к общему числу n всех элементарных исхо-дов (событий), образующих полную группу попарно несовместных и равновозможных событий и записывают: Свойства вероятности: 1.Вероятность достоверного события=1 (при m=n): 2.Вероятность невозможного события=0 (при m=0): 3.Вероятность случайного события заключена в пределах: Геометрическая вероятность Пусть имеется пространство событий, элементарные исходы которого можно представить в виде точек, заполняющих нек. область Ω в пространстве R 3. Если при этом событию А благоприятствуют элемен-тарные события, заполняющие нек. подоб-ласть D из Ω, то геометр. вероятностью события А наз. отношение объема области D к объему области Ω: Аналогично определяется геометр. вероят-ность события, когда множ-во Ω представ-ляет собой нек. область на плоскости или отрезок на прямой линии. В этих случаях объемы областей заменяются, соответст-но, площадями фигур или длинами отрезков. Случайное событие – событие, которое может произойти (не произойти), если будет выполнена определённая совок-сть условий S, которая наз. испытанием. Несколько событий наз совместными, если в результате испытания появление 1-го из них не исключает появления другого в одном и том же испытании.
Несколько событий наз несовместными, если в результате испытания появ-ление 1-го из них исключает появление других (остальных) событий в одном и том же испытании (выпадение очков на игральной кости – 6 несовмес. событий).
2 события наз. равновозможными, если нет оснований считать, что появление одного из них более возможно, чем появление другого. (выбрасывание орла и решки - равновозможные события). Полная группа событий – совок-сть случаных событий, если в результате испытания появится хотя бы 1 из них. С=
Для решения вероятностных задач используют формулы комбинаторики: 1) число перестановок Pn из n элементов равно: Перестановки – комбинации, которые можно составить из n эл-тов по n эл-тов в каждой, чтобы они отличались только порядком расположения этих эл-тов. 2) число размещений Размещение – комбинации, которым можно составить из n эл-тов по m эл-тов в каждой и отличающихся друг от друга либо составом эл-тов, либо порядком расположения эл-тов. 3) число различных сочетаний Сочетания – комбинации, которые можно составить из n эл-тов по m эл-тов в каждой и отличающихся друг от друга только составом эл-тов. Правило суммы Если объект А может быть извлечён из нек. совок-сти объектов m способами, а объект В может быть извлечён из совок-сти объектов n способами, то извлечь объект А и объект В (либо А, либо В) можно n+m способами Правило произведения Если объект А может быть извлечён из нек. совок-сти объектов m способами и для каждого способа извлечения объекта А объект В может быть извлечён n способами, то извлечь объект А, и объект В можно nm способами.
Суммой событий А и В наз. событие С = А + В, состоящее в наступлении хотя бы 1-го из этих событий. Если А и В – несовместные, то А+В – это событие, состоящее в наступлении либо события А, либо события В.
Если А и В – совместные, то А+В – это события, состоящие в наступлении либо события А, либо события В, либо события АВ (и А, и В).
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |


 Область сх-cти:
Область сх-cти:  .
.





 .
. .
. ,
, ,(2)
,(2)  ,(3)
,(3)  . (4)
. (4)


 (2.36)
(2.36)










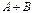 или
или  – сумма событий А и В (событие, которое заключается в том, что происходит либо событие А, либо событие В, либо события и А и В).
– сумма событий А и В (событие, которое заключается в том, что происходит либо событие А, либо событие В, либо события и А и В). или
или  – произведение собы-тий (событие, которое состоит в том, что одновременно происходят события А и В).
– произведение собы-тий (событие, которое состоит в том, что одновременно происходят события А и В). - противоположное событию А (если эти события несовместны, а их сумма – достоверное событие)-(Промах или попадание про стрельбе по мишени)
- противоположное событию А (если эти события несовместны, а их сумма – достоверное событие)-(Промах или попадание про стрельбе по мишени)
 m элементов из
m элементов из 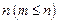 равно:
равно: 
 m элементов из n равно
m элементов из n равно 




