Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
График норм. закона распредел.Содержание книги
Поиск на нашем сайте
Если Вероятность попадания непрерывной СВ X, распределённой нормально в интервале (
где Предположим, нормально распределёная непрерывная СВ X будет удовлетворять неравенству
Правило трёх сигм: если непрерывная СВ Х распределена по нормальному закону, то отклонение её возможных значений от её мат. ожида-ния не превысит утроенного среднего квадратического отклонения.
Центральная предельная теорема: если СВ Х представляет собой сумму очень большого числа взаимонезависимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то СВ Х распределена по нормальному закону (по закону близкому к нормальному).
Для числовой хар-стики двумерной СВ (Х, Y) используют числовые хар-стики её составляющих:
=> Если X и Y – независимые СВ, то
Корренированной наз. СВ Х и Y, если их корреляционный момент Следствия: 1. из независ-сти => их некоррен-нность 2. из некоррен-сти => их независ-сть 3. из корреннир-сти => зависимость 4. из завис-сти => их корренир-сть
46. Выборка – совок-сть случайно отобранных объектов. Объем выборки - число отобранных значений. Генер. совок-сть – совок-сть объектов, из которых производится выборка. При исследовании количественного или качественного признака СВ Х из общего числа возможных значений (генераль- ной совок-сти) извлекается случайным образом нек. число эл-тов. Эту совокупность элементов называют случайной выборкой или просто выборкой, а число n отобранных значений – объемом выборки. Результаты всякого эксперимента запи- сывают в виде таблицы, в первой строке которой указывают номер эксперимента, а во второй – значение наблюдаемого признака Х, равное Если mi – число наблюдений значения xi признака Х, 46.Эмпирическая функция распределения выборки - функция
При больших объемах выборки интервал изменения всех ее вариант разбивают на определенное число интервалов равной длины, которые называются интервалами группировки. Затем подсчитывают число вариант выборки, попавших в каждый из интервалов, вычисляют относительные частоты числа вариант в каждом интервале. Таблица, в которой дана система интер-валов, указаны частоты или относительные частоты числа вариант в каждом интервале, наз. статистической совокупностью. Статистическую совокупность графически изображают с помощью гистограммы. Гистограмму строят следующим образом: по оси абсцисс откладывают интервалы, на каждом из них строят прямоугольники, площади которых равны частотам или относительным частотам попадания ва-риант в соответствующий интервал. Высо-ты этих прямоугольников равны
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.005 с.) |

 растёт, то кривая растягивается вдоль ОХ и сжимается вдоль OY. При изменении
растёт, то кривая растягивается вдоль ОХ и сжимается вдоль OY. При изменении 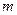 кривая смещается без иземения формы вдоль OX.
кривая смещается без иземения формы вдоль OX.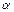 ,
, 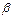 ) равна
) равна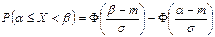
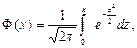 (1.25)
(1.25)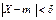 . Найдём вероят-ность
. Найдём вероят-ность 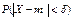 . Неравенство
. Неравенство 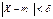 равносильно неравенству
равносильно неравенству 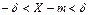 или
или  .
.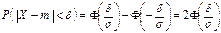 Получается, что вероятность заданного отклонения равна:
Получается, что вероятность заданного отклонения равна: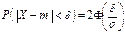 .
.
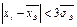
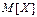 ,
,  ,
, 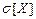 ,
, 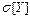 , а также для рассмотрения тесноты связи между составляющими используют корреляционный момент.
, а также для рассмотрения тесноты связи между составляющими используют корреляционный момент.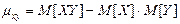
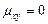 (теорема)
(теорема) 0, и наз. некорренированной, если
0, и наз. некорренированной, если  и называемое вариантой признака Х. Такая таблица наз. статистическим рядом. Статис-тический ряд, расположенный по воз-растанию вариант, наз. вариационным (x1, x2, …, xn).
и называемое вариантой признака Х. Такая таблица наз. статистическим рядом. Статис-тический ряд, расположенный по воз-растанию вариант, наз. вариационным (x1, x2, …, xn).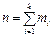 – общее число наблюдений (объем выборки), то число mi / n наз. относительной частотой наблюдения xi:
– общее число наблюдений (объем выборки), то число mi / n наз. относительной частотой наблюдения xi: 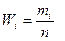 .
.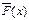 , определяю-щая для всякого
, определяю-щая для всякого  относительную частоту события
относительную частоту события 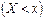 , т.е.
, т.е. 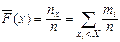 , где
, где 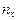 – число вариант, меньших x; n – объем выборки.
– число вариант, меньших x; n – объем выборки.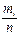 , или
, или 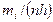 , где
, где 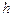 – длина выбранных интервалов. Полигоном частот наз. лома-ную линию, состоящую из отрезков, соеди-няющих точки
– длина выбранных интервалов. Полигоном частот наз. лома-ную линию, состоящую из отрезков, соеди-няющих точки