
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий достаточный признак сходимости знакопеременных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знакочередующийся ряд является частным случаем знакопеременного ряда. Числовой ряд Теорема. Пусть дан знакопеременный ряд Доказательство: Рассмотри вспомогательный ряд, составленный из членов рядов
Очевидно, что Отметим, что обратное утверждение несправедливо: если сходится ряд Пример. Исследовать сходимость ряда
Абсолютная и условная сходимость числовых рядов Знакопеременный ряд называют абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называют условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится. Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность). Т.е. абсолютно сходящиеся ряды суммируются, вычитаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов. В случае условно сходящихся рядов, такие свойства, вообще говоря, не имеют места.
VI.Степенные ряды Функциональные ряды Основные понятия Ряд, членами которого являются функции от Если полученный числовой ряд сходится, то точка Действительные или комплексные числа 1.2. Сходимость степенных рядов Область сходимости степенного ряда содержит, по крайней мере, одну точку: Теорема Абеля. Если степенной ряд сходится при Доказательство. По условию ряд Следствие. Если ряд (степенной) расходится при 1.3. Интервал и радиус сходимости степенного ряда Из теоремы Абеля следует, что, если Интервал Отметим, что на концах интервала сходимости (при Для нахождения радиуса сходимости степенного ряда можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда Аналогично, воспользовавшись радикальными признаками, можно установить, что Дополнение: 1) Если 2) Интервал сходимости степенного ряда по степеням 3) Если степенной ряд содержит не все степени Пример 1. Найти область сходимости ряда Пример 2. Найти область сходимости ряда 1.4. Свойства степенных рядов 1) Сумма 2) Степенные ряды 3) Степенной ряд внутри интервала сходимости можно почленно дифференцировать, при этом для ряда 4) Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для степенного ряда при
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 , содержащий бесконечное множество положительных и бесконечных множеств отрицательных членов, называется знакопеременным. Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.
, содержащий бесконечное множество положительных и бесконечных множеств отрицательных членов, называется знакопеременным. Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.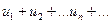 . Если сходится ряд
. Если сходится ряд  , составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.
, составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд. и
и 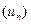 .
. .
. для всех
для всех  , но ряд
, но ряд 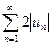 сходится в силу условий теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд
сходится в силу условий теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд  . Поскольку данный знакопеременный ряд представляет собой разность двух сходящихся рядов
. Поскольку данный знакопеременный ряд представляет собой разность двух сходящихся рядов  , то на основании свойства 2 числовых рядов ряд
, то на основании свойства 2 числовых рядов ряд 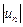 .
. . Для этого ряда выполнены условия признака Лейбница. Следовательно, ряд сходится. Однако ряд, составленный из модулей членов этого ряда, т.е.
. Для этого ряда выполнены условия признака Лейбница. Следовательно, ряд сходится. Однако ряд, составленный из модулей членов этого ряда, т.е.  расходится (гармонический ряд).
расходится (гармонический ряд). , называется функциональным.
, называется функциональным.  . Придавая
. Придавая  , который может быть как сходящимся, так и расходящимся.
, который может быть как сходящимся, так и расходящимся. называется точкой сходимости ряда, если ряд расходится – точкой расходимости. Совокупность числовых значений аргумента
называется точкой сходимости ряда, если ряд расходится – точкой расходимости. Совокупность числовых значений аргумента  . Определяется она в области сходимости ряда равенством
. Определяется она в области сходимости ряда равенством  , где
, где  - частичная сумма ряда. Среди функциональных рядов в математике и ее приложениях особая роль принадлежит рядам, членами которых являются степенные функции аргумента
- частичная сумма ряда. Среди функциональных рядов в математике и ее приложениях особая роль принадлежит рядам, членами которых являются степенные функции аргумента 
 ,
,  , …,
, …,  … называются коэффициентами ряда, а
… называются коэффициентами ряда, а 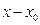 , т.е. ряд вида
, т.е. ряд вида  , где
, где  .
. , в которой ряд сходится.
, в которой ряд сходится. , то он абсолютно сходится при всех значениях
, то он абсолютно сходится при всех значениях  .
.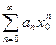 сходится. Следовательно, по необходимому признаку сходимости
сходится. Следовательно, по необходимому признаку сходимости  . Отсюда следует, что величина
. Отсюда следует, что величина  ограничена, т.е. найдется такое число
ограничена, т.е. найдется такое число  , что для всех
, что для всех 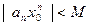 ,
,  . Пусть
. Пусть  и следовательно,
и следовательно,  ,
,  геометрической прогрессии. Поэтому по признаку сравнения при
геометрической прогрессии. Поэтому по признаку сравнения при  , то он расходится и при всех
, то он расходится и при всех  .
. есть точка сходимости степенного ряда, то интервал
есть точка сходимости степенного ряда, то интервал  весь состоит из точек сходимости данного ряда. При всех значениях
весь состоит из точек сходимости данного ряда. При всех значениях  называют интервалом сходимости степенного ряда. Положив
называют интервалом сходимости степенного ряда. Положив  , интервал сходимости можно записать в виде
, интервал сходимости можно записать в виде  . Число
. Число  называется радиусом сходимости степенного ряда, т.е.
называется радиусом сходимости степенного ряда, т.е.  - это такое число, что при всех
- это такое число, что при всех 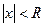 , ряд абсолютно сходится, а при
, ряд абсолютно сходится, а при  ряд расходится. В частности, когда степенной ряд сходится лишь в одной точке
ряд расходится. В частности, когда степенной ряд сходится лишь в одной точке  , то считаем, что
, то считаем, что  . Если же степенной ряд сходится при всех значениях
. Если же степенной ряд сходится при всех значениях  .
. и
и  и применим к нему признак Даламбера. Допустим, что существует предел
и применим к нему признак Даламбера. Допустим, что существует предел  ,
,  . По признаку Даламбера ряд сходится, если
. По признаку Даламбера ряд сходится, если  , т.е. ряд сходится при тех значениях
, т.е. ряд сходится при тех значениях 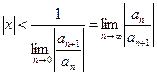 . Ряд, составленный из модулей членов степенного ряда, расходятся при тех значениях
. Ряд, составленный из модулей членов степенного ряда, расходятся при тех значениях  . Таким образом, для степенного ряда радиус абсолютной сходимости
. Таким образом, для степенного ряда радиус абсолютной сходимости  (1).
(1). (2).
(2). , то можно убедиться, что ряд степенной абсолютно сходится на всей числовой оси. В этом случае
, то можно убедиться, что ряд степенной абсолютно сходится на всей числовой оси. В этом случае  . Если
. Если  , то
, то  .
. находят из неравенства
находят из неравенства  и имеет вид
и имеет вид  .
. . Воспользуемся формулой (1)
. Воспользуемся формулой (1)  , следовательно данный ряд абсолютно сходится на всей числовой оси.
, следовательно данный ряд абсолютно сходится на всей числовой оси. . Данный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем
. Данный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем  ,
,  ;
;  . Ряд абсолютно сходится, если
. Ряд абсолютно сходится, если  или
или  . Исследуем поведение ряда на концах интервала сходимости. При
. Исследуем поведение ряда на концах интервала сходимости. При  имеем ряд
имеем ряд  , который сходится по признаку Лейбница. При
, который сходится по признаку Лейбница. При  имеем ряд
имеем ряд  , это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок
, это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок 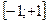 .
. степенного ряда является непрерывной функцией в интервале сходимости
степенного ряда является непрерывной функцией в интервале сходимости  .
. и
и  , имеющие радиусы сходимости соответственно R1 и R2, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности этих рядов не меньше, чем меньшее из чисел R1 и R2,.
, имеющие радиусы сходимости соответственно R1 и R2, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности этих рядов не меньше, чем меньшее из чисел R1 и R2,. при
при  выполняется равенство
выполняется равенство  (1)
(1) выполняется равенство
выполняется равенство  (2). Ряды (1) и (2) имеют тот же радиус сходимости, что и исходный степенной ряд. Свойства степенных рядов широко используются в теоретических исследованиях и приближенных расчетах.
(2). Ряды (1) и (2) имеют тот же радиус сходимости, что и исходный степенной ряд. Свойства степенных рядов широко используются в теоретических исследованиях и приближенных расчетах.


