
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I.Функции нескольких переменныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЧАСТЬ II I.Функции нескольких переменных Функции одной переменной не охватывают все зависимости существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных. В качестве примера функций нескольких переменных будем рассматривать функцию двух переменных, т.к. основные особенности таких многоаргументных зависимостей вполне проявляются и в этом случае. Функция двух переменных Пусть задано множество D упорядоченных пар чисел (х;у),и соответственно f, которое каждой паре чисел (х;у) сопоставляет только одно число Z, f =Z называется функция двух переменных определенной на множество D и записывается в виде Z= f(х;у). При этом х и у называются независимыми переменными (аргументами),а Z зависимой переменной (функцией)., множество D – называется областью определения функции. Примером такой функции может служить площадь прямоугольника Функция двух переменных, как и функции одной переменной может быть задана разными способами (табличный, графический и аналитический). Мы, как правило, будем пользоваться аналитическим способом, когда функция задается с помощью формулы.
Z= f(х; у) называется непрерывной в точке М0(х0,у0), если она: а) определена в этой точке и некоторой ее окрестности. б) имеет предел в) этот предел равен значению функции в точке М0, т.е. Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, называются точками разрыва этой функции. Точки разрыва могут образовывать целую линию разрыва. Так, функция
а) частные производные первого порядка. Пусть задана функция Z= f(х; у). Т.к. х и у – независимые переменные, то одна из них может меняться, а вторая сохранять свое значение. Дадим х приращение ∆х, сохраняя у=const. Тогда ∆хZ=f(x+∆x,y)-f(x,y). Аналогично получим ∆у Z=f(х,у+∆у)- f(x,y). Полное приращение функции ∆Z=f(x+∆x,у+∆y)-f(x,y). Если существует предел
Если Z= f(х;у) имеет частные производные Теорема. Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой, т.е. Z″xy=Z″yx.
Пусть Z= f(х;у) определена в некоторой окрестности точки М(х;у) полное приращение ∆Z=f(x+∆x,у+∆у)-f(x,y). Z= f(х;у) называется дифференцируемой в М(х;у), если ее полное приращение можно представить в виде: ∆Z=А∆х+В∆у+α∆х+β∆у, где α= α(∆х,∆у)→0 и β= β(∆х,∆у)→0 при ∆х→0, ∆у→0. Сумма двух первых слагаемых представляет собой главную часть приращения функции. Главная часть приращения функции, линейная относительно ∆х и ∆у, называется полным дифференциалом функции и обозначается символом dZ=A∆x+B∆y. Выражения A∆x и B∆y называются частными дифференциалами. Для независимых переменных х и у полагают ∆x=dx, ∆y=dy. Поэтому dZ=Adx+Bdy. Теорема 1. (необходимое условие дифференцирования функции). Если Z= f(х;у) дифференцируема в точке М(х;у), то она непрерывна в этой точке и имеет в ней частные производные
Таким образом, можно записать dZ= Теорема 2. Если Z= f(х; у) имеет непрерывные частные производные Z′х и Z′у в точке М (х;у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой записанной выше. Чтобы функция Z= f(х; у) была дифференцируема в точке, необходимо чтобы она имела в ней частные производные и достаточно чтобы она имела в точке непрерывные частные производные. Арифметические свойства правила исчисления дифференциалов функции одной переменной сохраняются и в случае дифференциалов функции двух и более переменных.
Полный дифференциал называется дифференциалом первого порядка. Пусть Z= f(х;у) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка в этом случае определяется по формуле d3 Z= d (d2 Z)==(
Пусть Z= f(х;у) – функция двух переменных х и у, каждая из которых является функцией независимой переменной t (х=х(t),у=у(t)). В этом случае Z= f(х(t);у(t)) является сложной функцией одной независимой переменной t, а переменные х и у – являются промежуточными переменными. Теорема. Если Z= f(х;у) дифференцируема в точке М(х,у) и х=х(t),у=у(t) – дифференцируемые функции независимой переменной t, то производная сложной функции Z(t)= f(х(t);у(t)) вычисляется по формуле Доказательство. Дадим независимой t приращение ∆t. Тогда х=х(t) и у=у(t) получат приращения ∆х и ∆у соответственно. Они в свою очередь вызовут приращение ∆Z функции Z. Так как Z= f(х;у) по условию дифференцируемая в М(х,у), то ее полное приращение равно ∆Z= 8.Инвариантность формы полного дифференциала Используя правила дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности, т.е. сохраняет один и тот же вид, независимо от того являются ли аргументы независимыми переменными или функциями независимых переменных. Пусть Z= f(х;у), где x, y – независимые переменные, тогда полный дифференциал (1ого порядка) имеет вид dZ= Рассмотрим сложную функцию Z= f(х; у), где x=x(u, Z= f(x(u,
dZ= Выражения в скобках представляют собой полные дифференциалы dx и dy функции x=x(u,
Функция Z= f(х; у) называется неявной, если она задается уравнением F(x,y,z)=0 неразрешенным относительно Z. Найдем частные производные
Откуда Пример: Найти частные производные функции Z заданной уравнением Здесь F(x,y,z)=
Пусть функция двух переменных Z= f(x; у) задана в некоторой окрестности т. М (x, y). Рассмотрим некоторое направление, определяемое единичным вектором
Рис. 1 Если функция Z дифференцируема в точке
и переходя к пределу при
Рассмотрим функцию трех переменных Градиентом этой функции
Поскольку единичный вектор
Понятия max, min, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной переменной. Пусть функция Z= f(x; у) определена в некоторой области D и т. М
Теорема: (Необходимые условия экстремума). Если в точке М
Доказательство: зафиксировав одну из переменных x или y, превратим Z= f(x; у) в функцию одной переменной, для экстремума которой вышеописанные условия должны выполняться. Геометрически равенства Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Например, при Z=xy точка O(0,0) является критической. Однако экстремума в ней функция Z=xy не имеет. (Т.к. в I и III четвертях Z>0, а в II и IV – Z<0). Таким образом для нахождения экстремумов функции в данной области необходимо подвергнуть каждую критическую точку функции дополнительному исследованию. Теорема: (Достаточное условие экстремумов). Пусть в стационарной точке
Тогда: 1) если 2) если В случае если
II. Неопределенный интеграл
В дифференцируемом исчислении мы решали задачу как по данной функции f(x) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F(x) – называется первообразной функции f(x) на интервале (a, b), если для любого Например, первообразной функции Очевидно, что первообразными будут также любые функции Теорема 1. Если F(x) является первообразной функции f(x) на Док-во. Функция Множество всех первообразных функций Здесь
Таблица основных неопределенных интегралов Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла. Например: т.к. Ниже приводимый список интегралов называется табличным. Необходимо отметить, что в приводимой ниже таблице переменная интегрирования может обозначать как независимую переменную, так и функцию от независимой переменной. Таблица основных интегралов.
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) В справедливости приведенных выше формул можно убедиться, взяв дифференциал правой части, который будет равен подынтегральному выражению в левой части формулы. Работа переменной силы Пусть материальная точка перемещается под действием силы F, направленной вдоль оси OX и имеющей переменную величину
Точность этого равенства возрастает с уменьшением
Формулы Ньютона-Лейбница Пусть Теорема: Если Доказательство: Для этого отрезок Преобразуем каждую разность в скобках по формуле Лагранжа Получим: т.е.
Формула Ньютона-Лейбница позволяет получить удобный способ вычисления определенных интегралов. Чтобы вычислить определенный интеграл от неправильной функции на отрезке Пример:
Несобственные интегралы Определенный интеграл 1) Интеграл с бесконечным промежутком интегрирования (несобственный интеграл 1ого порядка). Пусть функция В этом случае говорят, что несобственный интеграл сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интеграл Аналогичным образом определяется несобственный интеграл на промежутке
Пример: вычислить несобственный интеграл. а) б) 2) Интеграл от разрывной функции (несобственный интеграл 2ого рода) Пусть функция
Пример: Вычислить
Вычисление объема тела а) Вычисление объема тела по известным площадям параллельных сечений.
Через произвольную точку
Пример: Найти объем эллипсоида | |||||||
|
| Поделиться: |

 , треугольника
, треугольника  и т.д.
и т.д. Это понятие вводится аналогично случаю одной переменной. Для этого надо ввести понятие окрестности точки, (δ-окрестность точки М0(х0,у0)). Это будут все внутренние точки круга с центром в М0 и радиусом δ. Итак, пусть f(х; у) =.Z определена в некоторой окрестности точки М0(х0,у0), кроме, может быть, этой самой точки. Число А называется пределом Z= f(х; у) при х→х0 и у→у0, если для любого
Это понятие вводится аналогично случаю одной переменной. Для этого надо ввести понятие окрестности точки, (δ-окрестность точки М0(х0,у0)). Это будут все внутренние точки круга с центром в М0 и радиусом δ. Итак, пусть f(х; у) =.Z определена в некоторой окрестности точки М0(х0,у0), кроме, может быть, этой самой точки. Число А называется пределом Z= f(х; у) при х→х0 и у→у0, если для любого  >0 существует δ>0, такое, что для всех х≠х0 и у≠у0 удовлетворяющих неравенству
>0 существует δ>0, такое, что для всех х≠х0 и у≠у0 удовлетворяющих неравенству  <δ выполняется неравенство │f(x,y)-A│<
<δ выполняется неравенство │f(x,y)-A│< 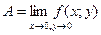 или
или 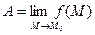


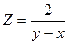 имеет линию разрыва у=х.
имеет линию разрыва у=х. , то он называется частной производной функции Z= f(х;у) в точке М(х;у) по переменной х и обозначается Z′x,
, то он называется частной производной функции Z= f(х;у) в точке М(х;у) по переменной х и обозначается Z′x,  ;
;  . Аналогично определяется и частная производная по у Z′=
. Аналогично определяется и частная производная по у Z′=  . Все частные производные находятся по формулам и правилам, полученным раннее для функций одной переменной и при условии, что или х или у – считаются const.
. Все частные производные находятся по формулам и правилам, полученным раннее для функций одной переменной и при условии, что или х или у – считаются const. и
и  и они являются функциями от (х,у), то их можно продифференцировать и получить частные производные второго порядка
и они являются функциями от (х,у), то их можно продифференцировать и получить частные производные второго порядка 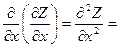 Z″xx;
Z″xx;  Z″xy;
Z″xy;  Z″yx и
Z″yx и  Z″yy; аналогичным образом можно ввести и определить частные производные 3, 4 и т.д. порядков. Частные производные, взятые по различным переменным, называются смешанными частными производными. Это Z″xy и Z″yx.
Z″yy; аналогичным образом можно ввести и определить частные производные 3, 4 и т.д. порядков. Частные производные, взятые по различным переменным, называются смешанными частными производными. Это Z″xy и Z″yx. и
и  , причем
, причем  . Найдем ее d2 Z= d(
. Найдем ее d2 Z= d( dx+
dx+  dy) dx+(
dy) dx+( dx+
dx+  dy)dу, отсюда d2 Z=
dy)dу, отсюда d2 Z=  )2Z. Аналогично можно получить формулу
)2Z. Аналогично можно получить формулу .
. , где α→0 β →0 при ∆х→0 и ∆у→0. Разделим ∆Z на ∆t и перейдем к пределу ∆t→0, тогда ∆х→0 и ∆у→0 в силу непрерывности функций х=х(t); у=у(t) получаем:
, где α→0 β →0 при ∆х→0 и ∆у→0. Разделим ∆Z на ∆t и перейдем к пределу ∆t→0, тогда ∆х→0 и ∆у→0 в силу непрерывности функций х=х(t); у=у(t) получаем:  , т.е.
, т.е. 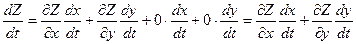 . Ч.т.д.
. Ч.т.д.
 ), y=y(u,
), y=y(u,  =
=  =(
=( )du+(
)du+( )d
)d 
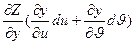
 функции Z заданной неявно. Для этого подставив в уравнение вместо Z функцию f(х;у) получим тождество F(x,y, f(х,у))=0. Частные производные по x и y функции, тождественно равной нулю, также равны нулю.
функции Z заданной неявно. Для этого подставив в уравнение вместо Z функцию f(х;у) получим тождество F(x,y, f(х,у))=0. Частные производные по x и y функции, тождественно равной нулю, также равны нулю. F(x, y, f (х, у)) =
F(x, y, f (х, у)) = 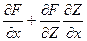 =0 (y считаем постоянным)
=0 (y считаем постоянным) F(x, y, f (х, у)) =
F(x, y, f (х, у)) =  =0 (x считаем постоянным)
=0 (x считаем постоянным) и
и 
 .
. ;
;  ;
;  ;
;  . По формулам приведенным выше имеем:
. По формулам приведенным выше имеем: и
и 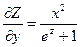
 , где
, где  (см. рис.1).
(см. рис.1).


 На прямой, проходящей по этому направлению через т. М возьмем т. М1 (
На прямой, проходящей по этому направлению через т. М возьмем т. М1 ( ) так, что длина
) так, что длина  отрезка MM1 равна
отрезка MM1 равна  . Приращение функции f(M) определяется соотношением
. Приращение функции f(M) определяется соотношением  , где
, где 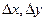 связаны соотношениями
связаны соотношениями  . Предел отношения
. Предел отношения 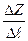 при
при  будет называться производной функции
будет называться производной функции 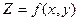 в точке
в точке  по направлению
по направлению  и обозначаться
и обозначаться 
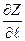 =
= 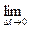
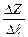 .
.  M1
M1 

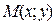






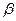





 поделив обе части на
поделив обе части на 
 , дифференцируемую в некоторой точке
, дифференцируемую в некоторой точке  .
. в этой точке. Для обозначения градиента используют символ
в этой точке. Для обозначения градиента используют символ 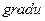 .
. 

 .
. .Градиент указывает направление наибыстрейшего роста функции в данной точке.
.Градиент указывает направление наибыстрейшего роста функции в данной точке.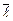 имеет координаты (
имеет координаты ( ), то производная по направлению для случая функции трех переменных записывается в виде
), то производная по направлению для случая функции трех переменных записывается в виде  , т.е.
, т.е.  имеет формулу скалярного произведения векторов
имеет формулу скалярного произведения векторов  и
и  , где
, где  - угол между вектором
- угол между вектором  , то отсюда следует, что производная функции по направлению принимает max значение при
, то отсюда следует, что производная функции по направлению принимает max значение при  , т.е., на самом деле градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке.
, т.е., на самом деле градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке. принадлежит к этой области. Точка М
принадлежит к этой области. Точка М  . Аналогичным образом определяется и точка min, только знак неравенства при этом изменится
. Аналогичным образом определяется и точка min, только знак неравенства при этом изменится 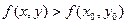 . Значение функции в точке max (min) называется максимумом (минимумом). Максимум и минимум функции называются экстремумами.
. Значение функции в точке max (min) называется максимумом (минимумом). Максимум и минимум функции называются экстремумами. ,
,  .
. ,
, 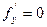 , называются стационарной точкой функции. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например Z=|-
, называются стационарной точкой функции. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например Z=|-  | имеет max в точке O(0,0), но не имеет в этой точке производных.
| имеет max в точке O(0,0), но не имеет в этой точке производных.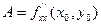 ,
,  и
и 

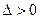 , то f(x; у) в точке
, то f(x; у) в точке  , то f(x; у) в точке
, то f(x; у) в точке 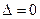 , экстремум в точке
, экстремум в точке  (или дифференциал). Искомую функцию F(x) называют первообразной функции f(x).
(или дифференциал). Искомую функцию F(x) называют первообразной функции f(x).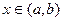 выполняется равенство
выполняется равенство  .
. является функция
является функция  , так как
, так как  .
.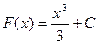 , где С – постоянная, поскольку
, где С – постоянная, поскольку  .
. , то множество всех первообразных для f(x) задается формулой
, то множество всех первообразных для f(x) задается формулой 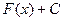 , где С – постоянное число.
, где С – постоянное число. . Пусть
. Пусть  некоторая другая отличная от
некоторая другая отличная от  первообразная функции
первообразная функции  , т.е.
, т.е.  =
= 
 , а это означает, что
, а это означает, что  , где С -
, где С -  . Следовательно,
. Следовательно,  .
. . Таким образом
. Таким образом  - подынтегральным выражением, x – переменной интегрирования,
- подынтегральным выражением, x – переменной интегрирования,  - знаком неопределенного интеграла. Операция нахождения неопределенного интеграла – интегрированием этой функции.
- знаком неопределенного интеграла. Операция нахождения неопределенного интеграла – интегрированием этой функции. , то
, то  .
.




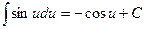





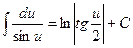







 . Найдем работу по перемещению точки М на
. Найдем работу по перемещению точки М на  .
.  . Для определения приближенного значения работы на всем участке
. Для определения приближенного значения работы на всем участке  , нам надо произвести суммирование на всем отрезке.
, нам надо произвести суммирование на всем отрезке. .
.
 .
. - функция, интегрируемая на
- функция, интегрируемая на  - непрерывна на отрезке
- непрерывна на отрезке  ), то имеет место соотношение
), то имеет место соотношение 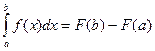 .
. на n отрезков. Введем средние точки для каждого из отрезков
на n отрезков. Введем средние точки для каждого из отрезков  . Рассмотрим соотношение
. Рассмотрим соотношение  .
. .
.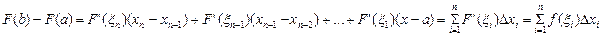 ,
,
 . Т.к.
. Т.к.  непрерывна на
непрерывна на 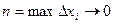 . Получим:
. Получим: .
. значений этой первообразной на концах отрезка
значений этой первообразной на концах отрезка  .
. , где промежуток интегрирования конечный, а подынтегральная функция непрерывна на
, где промежуток интегрирования конечный, а подынтегральная функция непрерывна на  непрерывна на промежутке
непрерывна на промежутке  . Если существует конечный предел
. Если существует конечный предел  ,то его называют несобственным интегралом первого порядка и обозначают
,то его называют несобственным интегралом первого порядка и обозначают  . Таким образом,
. Таким образом,  .
.  =
=  . Несобственный интеграл с двумя бесконечными пределами определяется формулой:
. Несобственный интеграл с двумя бесконечными пределами определяется формулой:
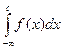 +
+  , где С – произвольное число. В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функция
, где С – произвольное число. В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функция  на промежутке
на промежутке  интеграл сходится
интеграл сходится интеграл расходится, т.к.
интеграл расходится, т.к. 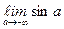 не существует.
не существует. , то его называют несобственным интегралом второго рода и обозначают
, то его называют несобственным интегралом второго рода и обозначают  . Таким образом, по определению
. Таким образом, по определению . Если функция
. Если функция 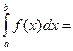
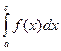 +
+  . В этом случае интеграл слева называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.
. В этом случае интеграл слева называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся. , при х=0, функция
, при х=0, функция 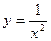 терпит бесконечный разрыв.
терпит бесконечный разрыв. . Следовательно, интеграл расходится.
. Следовательно, интеграл расходится. Пусть требуется найти объем тела V при известной площади S сечений этого тела относительно плоскости, перпендикулярной некоторой оси, например, ох;
Пусть требуется найти объем тела V при известной площади S сечений этого тела относительно плоскости, перпендикулярной некоторой оси, например, ох; 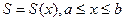 . Применим метод 2.
. Применим метод 2. проведем плоскость
проведем плоскость  , перпендикулярную оси ох. Обозначим через
, перпендикулярную оси ох. Обозначим через  площадь сечения тела этой плоскостью.
площадь сечения тела этой плоскостью.  обозначим объем части тела, лежащие левее плоскости
обозначим объем части тела, лежащие левее плоскости  величина v есть функция от
величина v есть функция от  )=0, v (
)=0, v ( )=v. Теперь найдем дифференциал функции v = v (x). Он представляет собой слой тела, заключенного между параллельными плоскостями, пересекающими ось
)=v. Теперь найдем дифференциал функции v = v (x). Он представляет собой слой тела, заключенного между параллельными плоскостями, пересекающими ось  в точках
в точках  , который можно приближено принять за цилиндр с основанием
, который можно приближено принять за цилиндр с основанием  (рис.5). поэтому дифференциал объема
(рис.5). поэтому дифференциал объема  . Тогда для нахождения полного объема это соотношение надо проинтегрировать в пределах от
. Тогда для нахождения полного объема это соотношение надо проинтегрировать в пределах от  - полученная формула называется формулой объема тела по площади параллельных сечений.
- полученная формула называется формулой объема тела по площади параллельных сечений. . Если эллипсоид рассечен плоскостью, параллельной плоскости
. Если эллипсоид рассечен плоскостью, параллельной плоскости  и на расстоянии
и на расстоянии 


