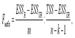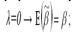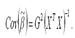Модели регрессии с переменной структурой. Фиктивные переменные

При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую принадлежность и др.).

Фиктивной переменной (dummy variable) называется атрибутивный или качественный фактор, представленный посредством определённого цифрового кода.

Наиболее наглядным примером применения фиктивных переменных является модель регрессии, отражающая проблему разрыва в заработной плате у мужчин и женщин.

Предположим, что на основе собранных данных была построена модель регрессии, отражающая зависимость заработной платы рабочих y от их возраста х:

yt=β0+β1xt.

Однако данная модель регрессии не может в полной мере охарактеризовать вариацию результативной переменной. Поэтому в модель необходимо ввести дополнительный фактор, например пол, на основании предположения о том, что у мужчин в среднем заработная плата выше, чем у женщин. В связи с тем, что переменная пола является качественной, её необходимо представить в виде фиктивной переменной следующим образом:

С учётом новой фиктивной переменной модель регрессии примет вид:

y=β0+β1x+β2D,

где β2 – это коэффициент, который характеризует в среднем разницу в заработной плате у мужчин и женщин.

Моделью регрессии с переменной структурой называется модель регрессии, которая включает в качестве факторной переменной фиктивную переменную.

Рассмотрим модель регрессии, характеризующую зависимость переменной размера заработной платы у от переменной стажа работников х с различным образованием. Качественная переменная «образование» может принимать три значения: среднее, среднее специальное и высшее. Для включения факторной переменной «образование» в модель регрессии, необходимо ввести две новых фиктивных переменных, потому что их количество должно быть на единицу меньше, чем значений качественной переменной.

Следовательно, качественная переменная «образование» может быть представлена в виде:

Модель регрессии, характеризующая зависимость переменной размера заработной платы у от переменной стажа работников х с различным образованием, примет вид:

y=β0+β1x+β2D1+ β3D2.

Моделью регрессии без ограничений (unrestricted regression) называется модель регрессии, в которую включены все фиктивные переменные.

Базисной моделью или регрессией с ограничениями (restricted regression) называется модель регрессии, в которой все значения фиктивных переменных равны нулю.

Для нашего примера модель регрессии вида y=β0+β1x+β2D1+β3D2 будет являться моделью регрессии без ограничений, а модель регрессии вида y=β0+β1x при D1= D2=0 будет являться моделью регрессии с ограничениями. Базисная модель регрессии соответствует регрессионной зависимости заработной платы рабочих со средним образованием от стажа работы.

Для модели регрессии без ограничений можно также построить частные регрессии. Например, частная модель регрессии переменной заработной платы работников со средним специальным образованием от переменной стажа:

y=β0+β1x+β2D1,

где β2 — это коэффициент, который характеризует, насколько большую заработную плату получают рабочие со средним специальным образованием по сравнению с работниками со средним образованием при одинаковом стаже работы.

Частная модель регрессии переменной заработной платы работников с высшим образованием от переменной стажа:

y=β0+β1x+β3D2,

где β3 – это коэффициент, который характеризует, насколько большую заработную плату получают рабочие с высшим образованием по сравнению с рабочими со средним образованием при одинаковом стаже работы.

Оценки неизвестных коэффициентов моделей регрессии с переменной структурой рассчитываются с помощью классического метода наименьших квадратов.

Тест Чоу

Предположим, что на основе собранных данных была построена модель регрессии. Перед исследователем стоит задача о том, стоит ли вводить в полученную модель дополнительные фиктивные переменные или базисная модель является оптимальной. Данная задача решается с помощью метода или теста Чоу. Он применяется в тех ситуациях, когда основную выборочную совокупность можно разделить на части или подвыборки. В этом случае можно проверить предположение о большей эффективности подвыборок по сравнению с общей моделью регрессии.

Будем считать, что общая модель регрессии представляет собой модель регрессии модель без ограничений. Обозначим данную модель через UN. Отдельными подвыборками будем считать частные случаи модели регрессии без ограничений. Обозначим эти частные подвыборки как PR.

Введём следующие обозначения:

PR1 – первая подвыборка;

PR2 – вторая подвыборка;

ESS(PR1) – сумма квадратов остатков для первой подвыборки;

ESS(PR2) – сумма квадратов остатков для второй подвыборки;

ESS(UN) – сумма квадратов остатков для общей модели регрессии.

– сумма квадратов остатков для наблюдений первой подвыборки в общей модели регрессии;

– сумма квадратов остатков для наблюдений второй подвыборки в общей модели регрессии.

Для частных моделей регрессии справедливы следующие неравенства:

Условие (ESS(PR1)+ESS(PR2))= ESS(UN) выполняется только в том случае, если коэффициенты частных моделей регрессии и коэффициенты общей модели регрессии без ограничений будут одинаковы, но на практике такое совпадение встречается очень редко.

Основная гипотеза формулируется как утверждение о том, что качество общей модели регрессии без ограничений лучше качества частных моделей регрессии или подвыборок.

Альтернативная или обратная гипотеза утверждает, что качество общей модели регрессии без ограничений хуже качества частных моделей регрессии или подвыборок

Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.

Наблюдаемое значение F-критерия сравнивают с критическим значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора.

Критическое значение F-критерия Фишера определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости а и двух степеней свободы свободы k1=m+1 и k2=n-2m-2.

Наблюдаемое значение F-критерия рассчитывается по формуле:где ESS(UN)– ESS(PR1)– ESS(PR2) – величина, характеризующая улучшение качества модели регрессии после разделения её на подвыборки;

m – количество факторных переменных (в том числе фиктивных);

n – объём общей выборочной совокупности.

При проверке выдвинутых гипотез возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл>Fкрит, то основная гипотеза отклоняется, и качество частных моделей регрессии превосходит качество общей модели регрессии.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т.е. Fнабл≤Fкрит, то основная гипотеза принимается, и разбивать общую регрессию на подвыборки не имеет смысла.

Если осуществляется проверка значимости базисной регрессии или регрессии с ограничениями (restricted regression), то выдвигается основная гипотеза вида:

Справедливость данной гипотезы проверяется с помощью F-критерия Фишера-Снедекора.

Критическое значение F-критерия Фишера определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости а и двух степеней свободы свободы k1=m+1 и k2=n–k–1.

Наблюдаемое значение F-критерия преобразуется к виду:

При проверке выдвинутых гипотез возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза отклоняется, и в модель регрессии необходимо вводить дополнительные фиктивные переменные, потому что качество модели регрессии с ограничениями выше качества базисной или ограниченной модели регрессии.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл≤Fкрит, то основная гипотеза принимается, и базисная модель регрессии является удовлетворительной, вводить в модель дополнительные фиктивные переменные не имеет смысла.

Спецификация переменных

Спецификацией переменных называется процесс отбора наиболее важных факторных переменных при построении модели регрессии.

Если в процессе эконометрического моделирования была осуществлена неправильная спецификация переменных, то это может привести к негативным последствиям, среди которых особо можно выделить два пункта:

1) из модели регрессии могут быть исключены факторные переменные, оказывающие наибольшее влияние на результативную переменную;

2) в модель регрессии могут быть включены факторные переменные, практические не связанные с результативной переменной или оказывающие на неё незначительное воздействие.

Предположим, что на основе собранных данных была построена нормальная модель множественной регрессии вида:

Y=Xβ+ε(1)

Данную модель можно рассматривать как базисную или ограниченную модель регрессии между исследуемыми переменными.

Тогда неограниченная модель данной регрессионной зависимости будет иметь вид:

Y=Xβ+Zλ+ε(2)

где Y – вектор результативных переменных;

X – вектор количественных факторных переменных;

Z – некоторая фиктивная переменная;

Β, λ – вектор неизвестных коэффициентов модели регрессии без ограничений, подлежащих оцениванию.

Рассмотрим случай исключения факторных переменных, оказывающих наибольшее влияние на результативную переменную, из модели регрессии.

Предположим, что модель регрессии с ограничениями является значимой. Исходя из этого условия, рассчитаем оценку коэффициента β, полученную методом наименьших квадратов, в оцениваемой модели регрессии с ограничениями (1):

Подставим в данную формулу вместо Y выражение Xβ+Zλ+ε:

Охарактеризуем полученную оценку коэффициента β модели регрессии с ограничениями с точки зрения свойства несмещённости. Для этого рассчитаем математическое ожидание оценки

где BIAS – это смещение оценки коэффициента β.

Таким образом, оценка

является смещённой, и устранить эту смещённость невозможно, даже при условии увеличения объёма выборочной совокупности.

Оценка коэффициента β модели регрессии с ограничениями (1) будет обладать свойством несмещённости в двух случаях:

1) если коэффициент при фиктивной переменной Z будет равен нулю:

2) при условии, что пропущенные переменные будут ортогонально включены в модель:

XTZ = 0.

Рассчитаем ковариацию оценки коэффициента β модели регрессии с ограничениями (1):

Матрица ковариаций МНК-оценок принимает такой вид только в том случае, если модель (1) является значимой.

Рассмотрим случай, когда в модель регрессии могут быть включены факторные переменные, практические не связанные с результативной переменной или оказывающие на неё незначительное воздействие.

Предположим, что модель регрессии без ограничений (2) является значимой. Исходя из этого условия, оценим коэффициенты модели регрессии с ограничениями (1).

Представим регрессионную модель с ограничениями (1) в следующем виде:

Пусть W – это переменные (X,Z) модели регрессии. Тогда оценка коэффициента β модели регрессии без ограничений может быть записана следующим образом:

Охарактеризуем полученную оценку коэффициента β модели регрессии без ограничений с точки зрения свойства несмещённости. Для этого рассчитаем математическое ожидание оценки

Следовательно, оценка

является несмещённой оценкой коэффициента регрессии β модели (2). Если в данную модель включить один дополнительный фактор, то оценки уже включённых факторных переменных свойства несмещённости не утратят. Но если в модель регрессии будут включены много лишних параметров, то точность оценок будет падать.

Матрица ковариаций МНК-оценок модели регрессии без ограничений будет иметь вид:

Матрица ковариаций будет иметь такой вид только в случае значимости модели регрессии без ограничений.

Компоненты временного ряда

Временным рядом называется ряд наблюдаемых значений изучаемого показателя, расположенных в хронологическом порядке или в порядке возрастания времени.

Отдельно взятый временной ряд можно представить как выборочную совокупность из бесконечного ряда значений показателей во времени.

Уровнями временного ряда называются наблюдения

из которых состоит данный ряд.

Временной ряд называется моментным рядом, если уровень временного ряда фиксирует значение изучаемого показателя на определённый момент времени.

Временной ряд называется интервальным рядом, если уровень временного ряда характеризует значение показателя за определённый период времени.

Временной ряд называется производным рядом, если уровни ряда представлены в виде производных величин (средних или относительных показателей).

Исследование данных, представленных в виде временных рядов, преследует две основные цели:

1) характеристика структуры временного ряда;

2) прогнозирование будущих уровней временного ряда на основании прошлых и настоящих уровней.

Достижение поставленных целей возможно с помощью идентификации модели временного ряда.

Идентификацией модели временного ряда называется процесс выявления основных компонент, которые содержит изучаемый временной ряд.

Временные ряды могут содержать два вида компонент – систематическую и случайную составляющие.

Систематическая составляющая временного ряда является результатом воздействия постоянно действующих факторов.

Выделяют три основных систематических компоненты временного ряда:

1) тренд;

2) сезонность;

3) цикличность.

Трендом называется систематическая линейная или нелинейная компонента, изменяющаяся во времени.

Сезонностью называются периодические колебания уровней временного ряда внутри года.

Цикличностью называются периодические колебания, выходящие за рамки одного года. Промежуток времени между двумя соседними вершинами или впадинами в масштабах года определяют как длину цикла.

Систематические составляющие характеризуются тем, что они могут одновременно присутствовать во временном ряду.

Случайной составляющей называется случайный шум или ошибка, которая воздействует на временной ряд нерегулярно.

К основным причинам, по которым возникает случайный шум, относят факторы резкого и внезапного действия, а также действия текущих факторов.

Катастрофическими колебаниями называется случайный шум, в основе возникновения которого лежат факторы резкого и внезапного действия.

Шум, в основе возникновения которого лежит действие текущих факторов, может быть связан также с ошибками наблюдений.

Отдельный уровень временного ряда обозначается как yt. Его можно представить в виде функции от основных компонент временного ряда следующим образом:

yt=f(T,S,C,ε),

где T – это трендовая компонента,

S – это сезонная компонента,

C – это циклическая компонента,

ε – случайный шум.

Существует несколько основных моделей временных рядов, к которым относятся:

1) аддитивная модель временного ряда, в которой компоненты представляют собой слагаемые:

yt=Tt+St+Ct+εt;

2) мультипликативная модель временного ряда, в которой компоненты представляют собой сомножители:

yt=Tt*St*Ct*εt;

3) комбинированная модель временного ряда:

yt=Tt*St*Ct+εt.