В каких случаях при оценивании нелинейных моделей метод наименьших квадратов оказывается неприменимым?

y=αx^b+u. Аддитивный случайный член не дает нам прологарифмировать функцию данного вида.

Что делать, если модель не приводится к виду, допускающую использование

Метода наименьших квадратов?

Использовать метод оценивания нелинейной регрессии Бокса-Кокса по следующему алгоритму:

1. Преобразуем зависимую переменную по методу Зарембки

2. Рассчитываем новые переменные (преобразование Бокса-Кокса) при λ от 1 до 0.

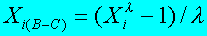
3. Рассчитываем регрессии для новых переменных при значениях λ от 1 до 0.

4. Выбираем минимальное значение суммы квадратов остатков (SSR), выбираем одну из крайних регрессий, к которой ближе точка минимума

ТЕМА 10. Интерпретация и использование нелинейных моделей парной регрессии.

Для чего нужны нелинейные эконометрические модели?

Нелинейные соотношения гораздо лучше подходят для описания многих экономических процессов, чем линейные.

Пример:

1. Анализ роста

Теоретический феномен – экономический рост

Анализ предпосылок: прирост пропорционален накопленному потенциалу

Формализация предпосылок:

Интерпретация и анализ: коэффициент регрессии «бета» - годовой темп роста, возможно сопоставление с реальными данными

2. описание кривых Энгеля, характеризующих соотношение между спросом на определённый товар Y и общей суммой дохода Х (подробное описание в 3-ем издании учебника Доугерти, стр.162-164).

Исходя из каких соображений и в каком порядке следует выбирать форму зависимости для эконометрической модели?

Из соображений графического соответствия, расчета эластичности и угла наклона, а также по тем соображениям, какая задача стоит перед нашей моделью и по теоретическим соответствиям о природе тех или иных зависимостей.

Выбираем из:

1. Линейные зависимости – самые простые зависисмости, всегда оставляем ее, если нет логического подтверждения необходимости иной спецификации.

2. Логарифмические зависимости – В зависимости от значений коэффициентов регрессии

Логарифмические зависимости отображают большое разнообразие форм, логарифмические зависимости помогают уменьшить масштаб переменных для их сравнимости.

3. Полулогарифмические зависимости – В зависимости от значений коэффициентов регрессии полулогарифмические зависимости отображают большое разнообразие форм с эффектом насыщения

4. Полиноминальные зависимости - Эти функции хорошо подходят для моделирования эффекта масштаба, анализа максимумов и минимумов

5. Обратные зависимости – Эти функции хорошо подходят для моделирования эффектов полного насыщения и ограниченности

 

Как интерпретируется коэффициент линейной формы регрессионной модели? Как можно обосновать справедливость предложенной интерпретации?

Линейная форма:

Интерпретация коэффициентов регрессии – предельный эффект независимого фактора.

Для полученных оценок уравнения регрессии

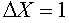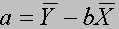
Т.е коэффициент регрессии показывает прирост результирующей переменной при изменении независимого фактора на единицу

 

В каких случаях оправдано использование линейной регрессии?

1. Если в этом есть экономический смысл

2. Если модель получилась формально качественной

Другой ответ:

В случае, когда необходимо рассчитать линейную связь между зависимой и независимой переменной, а затем использовать эту связь при прогнозировании, то есть используется для прогнозирования будущих значений параметра у исходя из имеющихся данных.

Как вычислить эластичности в каждой точке в случае использования линейной регрессии, и для чего можно использовать этот показатель?

E=(Δy/Δx)*x/y=bx/y. Для исследования того, является ли функция y=αx^b приемлемой.

Как интерпретируется коэффициент дважды логарифмической формы регрессионной модели? Как можно обосновать справедливость предложенной интерпретации?

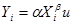=> Коэффициент интерпретируется следующим образом: эластичность Y по Х постоянна и равна .

На сколько % изменится y при изменении x на 1 %. dy/y=b*dx/x => b=(dy/dx)*x/y