Как можно проверить значимость линейного ограничения на основе знания сумм квадратов остатков модели без ограничения и модели с ограничением.
Похожие статьи вашей тематики
С помощью критерия F.
RSSR – сумма квадратов остатков с ограничением
RSSU – сумма квадратов остатков без ограничения
k – число объясняющих переменных в варианте без ограничения
Как можно проверить значимость линейного ограничения на основе знания коэффициентов детерминации модели без ограничения и модели с ограничением?
Проверка проводится по F -критерию или по t- критерию (непосредственно для включаемой переменной). Если регрессия без ограничений имеет m объясняющих переменных, то модель с ограничением l = m – 1. Поэтому F-стат имеет вид
Как формулируется нулевая гипотеза при проверке линейного ограничения?
Yi = α + β1 Xi1+... +βk Xk1 + ui
Н0: r1 * β1 +... + rk * βk = q
Какое из уравнений регрессии выбирается в случае, если линейное ограничение оказывается незначимым? Почему?
Выбирается уравнение с ограничением как более простое и обеспечивающее более эффективные оценки (с меньшими ошибками). (Немного странно, но так мне ответил Черняк. Просмотрите, кто соображает, если что, отпишитесь мне – Артём).
Какое из уравнений регрессии выбирается в случае, если линейное ограничение оказывается значимым? Почему?
Выбирается уравнение с ограничением, так как в этом случае принимается нулевая гипотеза о равенстве нулю всех дополнительных коэффициентов в уравнении без ограничений.
Как проверить одновременно несколько линейных ограничений?
Проверка аналогична проверке на добавление переменных. Т.е. есть одно уравнение с ограничением (restricted), и второе без ограничения (unrestricted), где у нас больше переменных. Тогда и проверяется сразу целесообразность добавления сразу нескольких переменных. Проверка проводится по F-критерию или по t-критерию (непосредственно для включаемой переменной).
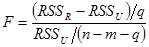
Плюс в программе можно провести тест Вальда, как на последнем семинаре.
В каких случаях и как использовать t-тест при проверке линейного ограничения?
ТЕМА 19. Оценивание нелинейных моделей множественной регрессии.
Какие основные виды нелинейных зависимостей используются в эконометрических моделях?
Логарифмическая
Полулогарифмическая
Степенная
В каких случаях используются полиномиальные формы регрессии? Какие экономические явления можно отобразить с помощью этих форм?
Когда модель в целом представляется линейной по своей природе (структуре), но включает в себя нелинейные элементы (например, облако распределения имеет форму параболы). Например, модель вида 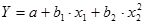 в сущности модель линейна, но при ее оценивании придется возводить независимую переменную в квадрат. Полиномиальные формы можно использовать для отображения основной тенденции развития социально-экономических явлений.
В чем состоят основные последствия неправильного выбора и использования функциональных форм?
Последствия данной ошибки таковы:
- Оценки могут быть смещенными;
- Ухудшение статистических свойств оценок или других показателей качества уравнения.
Эти последствия связаны с нарушением условий теорема Гаусса-Маркова для отклонений. Прогнозные качества модели с использованием неправильной функциональной формы очень низки.
Можно ли сравнивать статистическое качество различных функциональных форм уравнения регрессии?
Коэффициент детерминации (простой и исправленный) для различных функциональных форм несравним. На статистические характеристики уравнений смотреть можно.
Как оценить параметры производственной функции Кобба-Дугласа?
С помощью замены переменных.
Y = A Kα Lβ ν
ln Y = ln A + α ln K +β ln L+ ln ν
Как интерпретируются параметры производственной функции Кобба-Дугласа?
При увеличении одного их ресурсов (L или K) на 1% выпуск (Y) растет на α процентов (если K увеличился на 1%), или на β процентов (если L увеличился на 1 %).
Что означает условие постоянства эффекта масштаба? Как эконометрически может быть проверено это условие?
Условие постоянства масштаба означает, что Y в производственной функции Кобба-Дугласа изменяется в той же пропорции, что и K и L. Эконометрическая проверка:
- приводим уравнение к линейному виду:
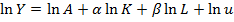
Для функции с постоянной отдачей от масштаба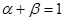 
тогда: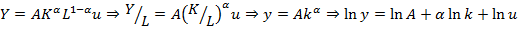 
|
