Каким образом можно оценить параметры функции кобба-дугласа с ограничением на эффект масштаба.

Функция Кобба-Дугласа имеет вид

Если сумма α+β равна единице — функция с постоянной отдачей от масштаба; если больше или меньше единицы, имеет место положительный или отрицательный эффекты масштаба соответственно.

Для оценки функции Кобба-Дугласа можно использовать метод наименьших квадратов. Её приводят к линейному виду, прологарифмировав обе части уравнения (как было показано в вопросе 109):

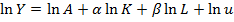
Для функции с постоянной отдачей от масштаба:

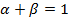
тогда: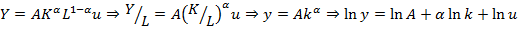

Каким образом можно учесть влияние технического прогресса в производственной функции Кобба-Дугласа?

При использовании агрегированных данных невозможно количественно оценить технический прогресс, проще всего включить экспоненциальный временной тренд в

уравнение, записав функцию Кобба—Дугласа в виде:

t — время; r — темп прироста выпуска благодаря техническому прогрессу.

 

После логарифмирования можно оценить коэффициенты:

(стр.157)

ЧАСТЬ ВТОРАЯ. ПОСТКОНТРОЛЬНАЯ.

Внимание – часть не редактировалась и не просматривалась!

ЛАГОВЫЕ ПЕРЕМЕННЫЕ

Что такое лаг и в чем он измеряется?

ЛАГ - запаздывание, экономический показатель, характеризующий временной интервал между двумя взаимосвязанными экономическими явлениями, одно из которых является причиной, а второе - следствием. Лаг измеряется в периодах, которые характеризуются данными переменными.

Лаговая переменная – это переменная, влияние которой характеризуется некоторым запаздыванием.

В чем состоит экономический смысл использования лаговых переменных в

Моделях регрессии?

Экономический смысл заключается в возможности существовании зависимости между оцениваемой переменной и независимыми переменными более ранних периодов. Например, можно предположить, что на расходы на жилье влияет личный располагаемый доход и индекс реальных цен более ранних периодов:

В каких случаях целесообразно использование лаговых переменных?

Использование лаговых переменных целесообразно, если оцениваемая переменная инерционна и медленно согласуется с изменениями независимых переменных.

Как изменяется число степеней свободы уравнения регрессии при использовании лаговых переменных?

Число степеней свободы уменьшается на число периодов запаздывания.

Как отражается на характеристиках модели включение дополнительных лаговых переменных?

Включение лаговых переменных приводит к появлению автокорелляции и, соответственно, к смещению оценок.

ФИКТИВНЫЕ ПЕРЕМЕННЫЕ

Что такое фиктивная переменная?

Фиктивная переменная – это переменная, вводимая для оценки влияния качественных факторов. Фиктивная переменная может принимать значение только 0 и 1.

Что такое «базовая категория»?

Эта категория при которой значения всех фиктивных переменных в уравнении равны нулю. Выбор базовой категории определяется набором проверок гипотез, которые хотелось бы провести.

Как определяется фиктивная переменная сдвига?

Фиктивная переменная сдвига просто добавляется к прочим параметрам уравнения:

249. Что такое структурный сдвиг в регрессионном анализе? (Точно не знаю)

Структурный сдвиг в регрессионном анализа – это различные оценки значений константы в уравнении регрессии для разных категорий, характеризующие значения фиктивными переменными.

Как определяется фиктивная переменная сдвига?

Вопрос 248

Как определяется фиктивная переменная наклона?

Фиктивная переменная наклона – это произведение фиктивной переменной на переменную наклон которой мы хотим найти. Причем фиктивная переменная наклона является отдельной объясняющей переменной:

, где Dx – это фиктивная переменная наклона.

Как определяется фиктивная переменная взаимодействия?

Фиктивная переменная взаимодействия выражает зависимость между отдельными группами фиктивных переменных и определяется так же, как и фиктивная переменная наклона - произведением двух фиктивных переменных разных групп:

, где UMD – это фиктивная переменная взаимодействия.