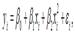Тесты Бокса-Кокса и Зарембеки выбора модели регрессии

Если в начале эконометрического моделирования перед исследователем стоит выбор между моделью регрессии, внутренне нелинейной и линейной моделью регрессии (или сводящейся к линейному виду), то предпочтение отдаётся линейным формам моделей.

Однако многие модели регрессии различной функциональной формы нельзя сравнивать с помощью стандартных критериев (например, сравнение по множественному коэффициенту детерминации, или суммам квадратов отклонений), которые позволили бы подобрать наиболее подходящую модель регрессии.

Например, если перед исследователем стоит вопрос о выборе линейной или логарифмической моделями регрессии, то использовать при этом критерий суммы квадратов отклонений нельзя, потому что общая сумма квадратов отклонений для логарифмической модели намного меньше, чем для линейной модели регрессии. Это вызвано тем, что значение логарифма результативной переменной logy намного меньше, чем соответствующее значение у, поэтому сравнение сумм квадратов отклонений моделей даёт неадекватные результаты.

Если сравнивать данные модели по критерию коэффициента множественной детерминации, то мы вновь получим неадекватные результаты. Коэффициент множественной детерминации для линейной модели регрессии характеризует объяснённую регрессией долю дисперсии результативной переменной у. Индекс детерминации для логарифмической модели регрессии характеризует объяснённую регрессией долю дисперсии переменной logy. Если значения данных критериев примерно равны, то сделать выбор между моделями регрессии с их помощью также не представляется возможным.

Одним из методов проверки предположения о возможной линейной зависимости между исследуемыми переменными является метод проверки гипотезы о линейной зависимости между переменными с помощью коэффициента детерминации r2 и индекса детерминации R2.

Другим методом выбора функциональной зависимости между переменными является тест Бокса-Кокса.

Предположим, что перед исследователем стоит задача выбора между линейной и логарифмической моделями регрессии. Рассмотрим применение теста Бокса-Кокса на данном примере.

Тест Бокса-Кокса основывается на утверждении о том, что (у-1) и logy являются частными случаями функции вида

В том случае, если параметр λ равен единице, то данная функция принимает вид F=y-1.

В том случае, если параметр λ стремиться к нулю, то данная функция принимает вид F=logy.

Для того чтобы определить оптимальное значение параметра λ, необходимо провести несколько серий экспериментов с множеством значений данного параметра. С помощью такого перебора можно рассчитать такое значение параметра λ, которое даст минимальную величину критерия суммы квадратов отклонений. Подобный метод вычисления оптимального значения параметра называется поиском на решётке или на сетке значений.

П. Зарембеки разработал один из вариантов теста Бокса-Кокса специально для случая выбора между линейной и логарифмической моделями регрессии.

Суть данного теста заключается в том, что к результативной переменной у применяется процедура масштабирования. Подобное преобразование в дальнейшем позволит сравнивать величины сумм квадратов отклонений линейной и логарифмический моделей регрессий.

Тест Зарембеки реализуется в несколько шагов:

1) рассчитывается среднее геометрическое значений результативной переменной у по формуле:

2) все результативные переменные у масштабируются по формуле:

где ỹ i – масштабированное значение результативной переменной у для i -го наблюдения;

3) оценивается линейная модель регрессии с использованием масштабированных значений ỹ i результативной переменной вместо у, и логарифмическая модель регрессии с использованием ỹ i вместо logy. Все факторные переменные и коэффициенты регрессии остаются при этом неизменными. После такого масштабирования результативных переменных значения сумм квадратов отклонений для данных моделей регрессии можно сравнивать между собой. Поэтому выбирается та модель регрессии, для которой данный критерий окажется наименьшим.

Коэффициенты эластичности

Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.

Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.

В общем случае коэффициент эластичности рассчитывается по формуле:

где

– первая производная результативной переменной у по факторной переменной x.

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня

если факторная переменная х изменится на 1 % относительного своего среднего уровня

Общая формула для расчёта коэффициента эластичности для среднего значения

факторной переменной х:

где

– значение функции у при среднем значении факторной переменной х.

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

yi=β0+β1xi,

средний коэффициент эластичности определяется по формуле:

Для полиномиальной функции второго порядка (параболической функции) вида:

средний коэффициент эластичности определяется по формуле:

Для показательной функции вида:

средний коэффициент эластичности определяется по формуле:

Для степенной функции вида:

средний коэффициент эластичности определяется по формуле:

Это единственная нелинейная функция, для которой средний коэффициент эластичности

равен коэффициенту регрессии β1.

Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х1.

Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х1, если факторная переменная изменится на 1 % относительно заданного уровня х1.

Общая формула для расчёта коэффициента эластичности для заданного значения х1 факторной переменной х:

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

yi=β0+β1xi,

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение линейной функции в точке х1.

Для полиномиальной функции второго порядка (параболической функции) вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение параболической функции в точке х1.

Для показательной функции вида:

точечный коэффициент эластичности определяется по формуле:

Для степенной функции вида:

точечный коэффициент эластичности определяется по формуле:

Докажем данное утверждение.

Запишем точечный коэффициент эластичности для степенной функции вида

через первую производную результативной переменной по заданной факторной переменной x 1:

Следовательно, Э(x1) = β1, что и требовалось доказать.

Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.

Производственные функции

Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов.

Факторами производственной функции могут являться следующие переменные:

1) объём выпущенной продукции (в стоимостном или натуральном выражении);

2) объём основного капитала или основных фондов;

3) объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней);

4) затраты электроэнергии;

5) количество станков, потребляемое в производстве и др.

Однофакторные производственные функции (т. е. функции с одной факторной переменной) относятся к наиболее простым производственным функциям. В данном случае результативной переменной является объём производства у, который зависит от единственной факторной переменной х. В качестве факторной переменной может выступать любая из вышеназванных переменных.

Основными разновидностями однофакторных производственных функций являются:

1) линейная однофакторная производственная функция вида:

y=β0+β1x,

например, производственная функция зависимости объёма производимой продукции от величины затрат определённого ресурса. Линейная однофакторная производственная функция характеризуется двумя особенностями:

а) если величина факторной переменной х равна нулю, то объём производства у не будет нулевым, потому что y=β0 (β0 ›0);

б) объём произведённой продукции у неограниченно возрастает при увеличении затрат определённого фактора х на постоянную величину β1 (β1 ›0). Однако данное свойство линейной однофакторной производственной функции чаще всего справедливо только на практике;

2) параболическая однофакторная производственная функция вида:

при условиях β0 ›0, β1 ›0, β2 ›0.

Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля;

3) степенная однофакторная производственная функция вида:

при условиях β0 ›0, β1 ›0.

Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений;

4) показательная однофакторная производственная функция вида:

при условиях 0‹ β1 ‹0.

Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β0.

5) гиперболическая однофакторная производственная функция вида:

Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства.

Двухфакторные производственные функции (функции с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу.

Для наглядного изображения двухфакторных производственных функций строят графики семейства кривых, основанных на различном сочетании двух факторов, но дающих в результате одно и то же значение объёма выпуска продукции. Кривые, построенные на основании равенства f(x1,x2)=const, называются изоквантами.

Изоквантой называется сочетание минимально необходимых ресурсных затрат для заданного уровня объёма производства.

Многофакторные производственные функции используются для изучения зависимости объёма производства от n -го количества факторов производства.

Общий вид многофакторной производственной функции:

y=f(xi),

где