
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели качества регрессииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проверка статистического качества оцененного уравнения регрессии проводится, с одной стороны, по статистической значимости параметров уравнения, а с другой стороны, по общему качеству уравнения регрессии. Кроме этого, проверяется выполнимость предпосылок МНК. Рассмотрим первые два вида проверок. Некоторые предпосылки МНК и проверки их выполнимости будем рассматривать отдельно. Как и в случае парной регрессии, статистическая значимость параметров множественной линейной регрессии с р факторами проверяется на основе t- статистики:
где величина
и в этой матрице обозначим j- й диагональный элемент как Тогда выборочная дисперсия эмпирического параметра регрессии равна:
а для свободного члена выражение имеет вид:
если считать, что в матрице
Стандартные ошибки параметров регрессии равны
Полученная по выражению (20) t- статистика для соответствующего параметра имеет распределение Стьюдента с числом степеней свободы ( Если В противном случае Это не приведет к существенной потере качества модели, но сделает её более конкретной.
Строгую проверку значимости параметров можно заменить простым сравнительным анализом. Если Если
Если Если
Анализ значимости коэффициента
или
Если доверительный интервал не содержит нулевого значения, то соответствующий параметр является статистически значимым, в противном случае гипотезу о нулевом значении параметра отвергать нельзя. Для проверки общего качества уравнения регрессии используется коэффициент детерминации R2, который в общем случае рассчитывается по формуле:
Коэффициент детерминаци показывает, как и в парной регрессии, долю общей дисперсии у, объясненную уравнением регрессии. Его значения находятся между нулем и единицей. Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение у. Для множественной регрессии R2 является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R2. Действительно, каждая следующая объясняющая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной. В формуле (25) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону уменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объёме наблюдений n. Если число параметров ( Поэтому в числителе и знаменателе дроби в (25) делается поправка на число степеней свободы остаточной и общей дисперсии соответственно:
Поскольку величина (25), как правило, увеличивается при добавлении объясняющей переменной к уравнению регрессии даже без достаточных на то оснований, скорректированный коэффициент (26) компенсирует это увеличение путем наложения «штрафа» за увеличение числа независимых переменных. Запишем (26) следующим образом:
По мере роста р увеличивается отношение Из (27) очевидно, что Доказано, что Обычно приводятся данные как по R2, так и по Анализ статистической значимости коэффициента детерминации проводится на основе проверки нуль-гипотезы
Величина F при выполнении предпосылок МНК и при справедливости нуль-гипотезы имеет распределение Фишера. Из (28) видно, что показатели F и R2 равны или не равны нулю одновременно. Если Эквивалентный анализ может быть предложен рассмотрением другой нуль-гипотезы, которая формулируется как
Эту гипотезу можно назвать гипотезой об общей значимости уравнения регрессии. Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех р объясняющих переменных Проверка такой гипотезы осуществляется на основе дисперсионного анализа сравнения объясненной и остаточной дисперсий, т. е. нуль-гипотеза формулируется как
Здесь в числителе – объясненная (факторная) дисперсия в расчете на одну степень свободы (число степеней свободы равно числу факторов, т. е. р). В знаменателе – остаточная дисперсия на одну степень свободы. Её число степеней свободы равно (
Следует отметить, что выражение (29) эквивалентно (28). Это становится ясно, если числитель и знаменатель (29) разделить на общую СКО:
Поэтому методика принятия или отклонения нуль-гипотезы для статистики (29) ничем не отличается от таковой для статистики (28). Анализ статистики F позволяет сделать вывод о том, что для принятия гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии коэффициент детерминации R2 должен существенно отличаться от нуля. Его критическое значение уменьшается при росте числа наблюдений и может стать сколь угодно малым. Например, пусть при оценке регрессии с двумя объясняющими переменными по 30 наблюдениям R2 =0,65. Тогда
По таблицам критических точек распределения Фишера найдем
Предположение о незначимости связи отвергается и здесь. Другим важным направлением использования статистики Фишера является проверка гипотезы о равенстве нулю не всех коэффициентов регрессии одновременно, а только некоторой части этих коэффициентов. Это позволяет оценить обоснованность исключения или добавления в уравнение регрессии некоторых наборов факторов, что особенно важно при совершенствовании линейной регрессионной модели. Пусть первоначально построенное по n наблюдениям уравнение регрессии имеет вид (4), и коэффициент детерминации для этой модели равен
для которого коэффициент детерминации равен
В случае справедливости
Если величина (31) превосходит критическое Аналогичные рассуждения можно использовать и для проверки обоснованности включения новых k факторов. В этом случае рассматривается следующая статистика:
Если она превышает критическое значение Fкр., то включение новых факторов объясняет существенную часть не объясненной ранее дисперсии зависимой переменной. Поэтому такое добавление оправдано. Добавлять переменные, как правило, целесообразно по одной. Кроме того, при добавлении факторов логично использовать скорректированный коэффициент детерминации, т. к. обычный Кроме коэффициента детерминации
Границы его изменения те же, что и в парной регрессии: от 0 до 1. Чем ближе его значение к единице, тем теснее связь результативного признака со всем набором исследуемых факторов. Для линейного уравнения множественной регрессии формула индекса корреляции может быть представлена выражением:
где Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции или совокупного коэффициента корреляции. При линейной зависимости определение совокупного коэффициента корреляции возможно без построения регрессии и оценки её параметров, а с использованием только матрицы парных коэффициентов корреляции:
где Δ r – определитель матрицы парных коэффициентов корреляции:
а Δ r 11 – определитель матрицы межфакторной корреляции:
Определитель (37) остаётся после вычеркивания из матрицы коэффициентов парной корреляции первого столбца и первой строки, что и соответствует матрице коэффициентов парной корреляции между факторами.
Спецификация модели Все предыдущие рассуждения и выводы, касающиеся классической множественной регрессии, основывались на предположении, что мы имеем дело с правильной спецификацией модели. Под спецификацией модели в данном случае (т. е. для модели линейной множественной регрессии при выполнении предпосылок МНК) будем понимать выбор объясняющих переменных. В этой связи важное значение приобретает рассмотрение двух вопросов, имеющих смысл именно во множественной регрессии, когда исследователь имеет дело с несколькими факторами: возможная мультиколлинеарность факторов и частная корреляция. Последняя особенно тесно связана с процедурами пошагового отбора переменных. Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. Например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы. 2. Факторы не должны быть коррелированы между собой и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой взаимной корреляцией, когда, например, Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Так, в приведенной зависимости с двумя факторами предполагается, что факторы х1 и х2 независимы друг от друга, т. е. Как было сказано ранее, добавление нового фактора в регрессии приводит к возрастанию коэффициента детерминации и уменьшению остаточной дисперсии. Но эти изменения могут быть незначительны, и не каждый фактор целесообразно вводить в модель. Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы, исходя из сущности проблемы; на второй – анализируется матрица показателей корреляции и устанавливается, какие из факторов наиболее тесно связаны с результатом, а какие – между собой. Здесь эконометрист чаще всего сталкивается с проблемой мультиколлинеарности. Под полной мультиколлинеарностью понимается существование между некоторыми из факторов линейной функциональной связи. Количественным выражением этого служит то обстоятельство, что ранг матрицы Х меньше, чем ( В практике статистических исследований полная мультиколлинеарность встречается достаточно редко, т. к. её несложно избежать уже на предварительной стадии анализа и отбора множества объясняющих переменных. Реальная (или частичная) мультиколлинеарность возникает в случаях существования достаточно тесных линейных статистических связей между объясняющими переменными. Точных количественных критериев для определения наличия или отсутствия реальной мультиколлинеарности не существует. Тем не менее, существуют некоторые эвристические рекомендации по выявлению мультиколлинеарности. В первую очередь анализируют матрицу парных коэффициентов корреляции:
точнее, ту её часть, которая относится к объясняющим переменным. Считается, что две переменные явно коллинеарны, если В этом случае факторы дублируют друг друга, и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдаётся фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. Пусть, например, при изучении зависимости
Очевидно, что факторы х1 и х2 дублируют друг друга ( Другим методом оценки мультиколлинеарности факторов может служить определитель матрицы парных коэффициентов корреляции между факторами (37). Обоснованием данного подхода служат такие рассуждения. Если бы факторы не коррелировали между собой, то в определителе (37) все внедиагональные элементы равнялись бы нулю, а на диагонали стояли бы единицы. Такой определитель равен единице. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты межфакторной корреляции равны единице, то определитель такой матрицы равен нулю. Следовательно, чем ближе к нулю определитель (37), тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к единице величина (37), тем меньше мультиколлинеарность факторов. Для оценки значимости мультиколлинеарности факторов выдвигается гипотеза Доказано, что величина Если Другим методом выявления мультиколлинеарности является анализ коэффициентов множественной детерминации факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Например, коэффициент
где первый фактор взят в качестве результативного признака, а остальные факторы – как независимые переменные, влияющие на первый фактор. Чем ближе такой При этом рассчитывается статистика:
Если коэффициент Основные последствия мультиколлинеарности: 1. Большие дисперсии оценок. Это затрудняет нахождение истинных значений определяемых величин и расширяет интервальные оценки, ухудшая их точность. 2. Уменьшаются t -статистики коэффициентов, что может привести к неоправданному выводу о несущественности влияния соответствующего фактора на зависимую переменную. 3. Оценки коэффициентов по МНК и их стандартные ошибки становятся очень чувствительными к малейшим изменениям данных, т. е. они становятся неустойчивыми. 4. Затрудняется определение вклада каждой из объясняющих переменных в объясняемую уравнением регрессии дисперсию зависимой переменной. 5. Возможно получение неверного знака у коэффициента регрессии.
Единого подхода к устранению мультиколлинеарности не существует. Существует ряд методов, которые не являются универсальными и применимы в конкретных ситуациях. Простейшим методом устранения мультиколлинеарности является исключение из модели одной или нескольких коррелированных переменных. Здесь необходима осторожность, чтобы не отбросить переменную, которая необходима в модели по своей экономической сущности, но зачастую коррелирует с другими переменными (например, цена блага и цены заменителей данного блага). В некоторых случаях для устранения мультиколлинеарности достаточно увеличить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным. Это приведёт к сокращению дисперсии коэффициентов регрессии и увеличению их статистической значимости. Однако при этом можно усилить автокорреляцию, что ограничивает возможности такого подхода. В некоторых случаях изменение спецификации модели, например, добавление существенного фактора, решает проблему мультиколлинеарности. При этом уменьшается остаточная СКО, что приводит к уменьшению стандартных ошибок коэффициентов. В ряде случаев минимизировать либо вообще устранить проблему мультиколлинеарности можно с помощью преобразования переменных.
Например, пусть эмпирическое уравнение регрессии имеет вид:
где факторы коррелированы. Здесь можно попытаться определить отдельные регрессии для относительных величин:
Возможно, что в моделях, аналогичных (40), проблема мультиколлинеарности будет отсутствовать. Теперь рассмотрим другой вопрос, имеющий важное значение для проблем, связанных со спецификацией модели множественной регрессии. Это частная корреляция. С помощью частных коэффициентов корреляции проводится ранжирование факторов по степени их влияния на результат. Кроме того, частные показатели корреляции широко используются при решении проблем отбора факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции. Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в модель нового фактора к остаточной дисперсии, имевшей место до введения его в модель. Высокое значение коэффициента парной корреляции между исследуемой зависимой и какой-либо независимой переменной может означать высокую степень взаимосвязи, но может быть обусловлено и другой причиной, например, третьей переменной, которая оказывает сильное влияние на две первые, что и объясняет их высокую коррелированность. Поэтому возникает задача найти «чистую» корреляцию между двумя переменными, исключив (линейное) влияние других факторов. Это можно сделать с помощью коэффициента частной корреляции. Коэффициенты частной корреляции определяются различными способами. Рассмотрим некоторые из них.
Для простоты предположим, что имеется двухфакторная регрессионная модель:
и имеется набор наблюдений Тогда коэффициент частной корреляции между у и, например, 1. Осуществим регрессию у на 2. Осуществим регрессию х1 на х2 и константу и получим прогнозные значения: 3. Удалим влияние 4. Определим выборочный коэффициент частной корреляции между у и х1 при исключении х2 как выборочный коэффициент корреляции между ey и
Значения частных коэффициентов корреляции лежат в интервале Существует тесная связь между коэффициентом частной корреляции
где Описанная выше процедура обобщается на случай, когда исключается влияние нескольких переменных. Для этого достаточно переменную Другой способ определения коэффициентов частной корреляции – матричный. Обозначив для удобства зависимую переменную как х0, запишем определитель матрицы парных коэффициентов корреляции в виде:
Тогда частный коэффициент корреляции определяется по формуле:
где Существует ещё один способ расчета – по рекуррентной формуле. Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например,
Если исследователь имеет дело лишь с тремя–четырьмя переменными, то удобно пользоваться соотношениями (46). При больших размерностях задачи удобнее расчет через определители, т. е. по формуле (45). В соответствии со смыслом коэффициентов частной корреляции можно записать формулу:
При исследовании статистических свойств выборочного частного коэффициента корреляции порядка k следует воспользоваться тем, что он распределен точно так же, как и обычный парный коэффициент корреляции, с единственной поправкой: объём выборки надо уменьшить на k единиц, т. е. полагать его равным Пример. По итогам года у 37 однородных предприятий легкой промышленности были зарегистрированы следующие показатели их работы: у – среднемесячная характеристика качества ткани (в баллах), По исходным данным были подсчитаны выборочные парные коэффициенты корреляции:
Проверка статистической значимости этих величин показала отсутствие значимой статистической связи между результативным признаком и каждым из факторов, что не согласуется с профессиональными представлениями т
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.78.203 (0.019 с.) |

 , (20)
, (20)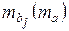 называется стандартной ошибкой параметра
называется стандартной ошибкой параметра  . Она определяется так. Обозначим матрицу:
. Она определяется так. Обозначим матрицу:
 .
. , (21)
, (21) (21’)
(21’) индексы изменяются от 0 до р. Здесь S 2 – несмещенная оценка дисперсии случайной ошибки ε:
индексы изменяются от 0 до р. Здесь S 2 – несмещенная оценка дисперсии случайной ошибки ε: . (22)
. (22) . (23)
. (23) ). При требуемом уровне значимости α эта статистика сравнивается с критической точкой распределения Стьюдента t (α;
). При требуемом уровне значимости α эта статистика сравнивается с критической точкой распределения Стьюдента t (α;  , то соответствующий параметр считается статистически значимым, и нуль-гипотеза в виде
, то соответствующий параметр считается статистически значимым, и нуль-гипотеза в виде  или
или  отвергается.
отвергается. параметр считается статистически незначимым, и нуль-гипотеза не может быть отвергнута. Поскольку
параметр считается статистически незначимым, и нуль-гипотеза не может быть отвергнута. Поскольку 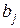 не отличается значимо от нуля, фактор
не отличается значимо от нуля, фактор 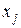 линейно не связан с результатом. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Не оказывая какого-либо серьёзного влияния на зависимую переменную, он лишь искажает реальную картину взаимосвязи. Поэтому после установления того факта, что коэффициент
линейно не связан с результатом. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Не оказывая какого-либо серьёзного влияния на зависимую переменную, он лишь искажает реальную картину взаимосвязи. Поэтому после установления того факта, что коэффициент 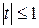 , т. е.
, т. е. 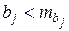 , то коэффициент статистически незначим.
, то коэффициент статистически незначим. , т. е.
, т. е.  , то коэффициент относительно значим. В данном случае рекомендуется воспользоваться таблицей критических точек распределения Стьюдента.
, то коэффициент относительно значим. В данном случае рекомендуется воспользоваться таблицей критических точек распределения Стьюдента. , то коэффициент значим. Это утверждение является гарантированным при
, то коэффициент значим. Это утверждение является гарантированным при  и
и  .
. , то коэффициент считается сильно значимым. Вероятность ошибки в данном случае при достаточном числе наблюдений не превосходит 0,001.
, то коэффициент считается сильно значимым. Вероятность ошибки в данном случае при достаточном числе наблюдений не превосходит 0,001. , определяется неравенством:
, определяется неравенством: (24)
(24) . (24’)
. (24’) . (25)
. (25) ) приближается к n, то остаточная дисперсия будет близка к нулю и коэффициент детерминации приблизится к единице даже при слабой связи факторов с результатом.
) приближается к n, то остаточная дисперсия будет близка к нулю и коэффициент детерминации приблизится к единице даже при слабой связи факторов с результатом. . (26)
. (26) . (27)
. (27) и, следовательно, возрастает размер корректировки коэффициента R2 в сторону уменьшения.
и, следовательно, возрастает размер корректировки коэффициента R2 в сторону уменьшения. при р > 1. С ростом р
при р > 1. С ростом р  растет медленнее, чем R2. Другими словами, он корректируется в сторону уменьшения с ростом числа объясняющих переменных. При этом
растет медленнее, чем R2. Другими словами, он корректируется в сторону уменьшения с ростом числа объясняющих переменных. При этом 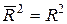 только при
только при  .
.  ). Поэтому для корректировки (26) нет строгого математического обоснования.
). Поэтому для корректировки (26) нет строгого математического обоснования. увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t- статистика для этой переменной по модулю больше единицы. Из этого отнюдь не следует, как можно было бы предположить, что увеличение
увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t- статистика для этой переменной по модулю больше единицы. Из этого отнюдь не следует, как можно было бы предположить, что увеличение 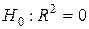 против альтернативной гипотезы
против альтернативной гипотезы  . Для проверки данной гипотезы используется следующая F- статистика:
. Для проверки данной гипотезы используется следующая F- статистика: . (28)
. (28) , то
, то  является наилучшей по МНК, и, следовательно, величина у линейно не зависит от
является наилучшей по МНК, и, следовательно, величина у линейно не зависит от  . Для проверки нуль-гипотезы при заданном уровне значимости α по таблицам критических точек распределения Фишера находится критическое значение
. Для проверки нуль-гипотезы при заданном уровне значимости α по таблицам критических точек распределения Фишера находится критическое значение  . Если
. Если  , нуль-гипотеза отклоняется, что равносильно статистической значимости R2, т. е.
, нуль-гипотеза отклоняется, что равносильно статистической значимости R2, т. е.  .
. .
.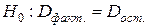 против альтернативной гипотезы
против альтернативной гипотезы 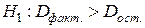 . При этом строится F- статистика:
. При этом строится F- статистика: . (29)
. (29) ), то число степеней свободы объясненной дисперсии равна разности
), то число степеней свободы объясненной дисперсии равна разности  , т. е. р.
, т. е. р. .
. .
. ;
;  . Поскольку Fнабл. =25,05> Fкр. как при 5%-м, так и при 1%-м уровне значимости, то нулевая гипотеза в обоих случаях отклоняется. Если в той же ситуации
. Поскольку Fнабл. =25,05> Fкр. как при 5%-м, так и при 1%-м уровне значимости, то нулевая гипотеза в обоих случаях отклоняется. Если в той же ситуации  , то
, то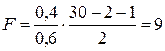 .
. . Исключим из рассмотрения k объясняющих переменных. Не нарушая общности, предположим, что это будут k последних переменных. По первоначальным n наблюдениям для оставшихся факторов построим другое уравнение регрессии:
. Исключим из рассмотрения k объясняющих переменных. Не нарушая общности, предположим, что это будут k последних переменных. По первоначальным n наблюдениям для оставшихся факторов построим другое уравнение регрессии: , (30)
, (30)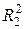 . Очевидно,
. Очевидно,  , т. к. каждая дополнительная переменная объясняет часть рассеивания зависимой переменной. Проверяя гипотезу
, т. к. каждая дополнительная переменная объясняет часть рассеивания зависимой переменной. Проверяя гипотезу  , можно определить, существенно ли ухудшилось качество описания поведения зависимой переменной. Для этого используют статистику:
, можно определить, существенно ли ухудшилось качество описания поведения зависимой переменной. Для этого используют статистику: . (31)
. (31)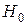 приведенная статистика имеет распределение Фишера с числом степеней свободы k и (
приведенная статистика имеет распределение Фишера с числом степеней свободы k и ( – потеря качества уравнения в результате отбрасывания k факторов; k – число дополнительно появившихся степеней свободы;
– потеря качества уравнения в результате отбрасывания k факторов; k – число дополнительно появившихся степеней свободы;  – необъясненная дисперсия первоначального уравнения.
– необъясненная дисперсия первоначального уравнения. на требуемом уровне значимости α, то нуль-гипотеза должна быть отклонена. В этом случае одновременное исключение из рассмотрения k объясняющих переменных некорректно, т. к.
на требуемом уровне значимости α, то нуль-гипотеза должна быть отклонена. В этом случае одновременное исключение из рассмотрения k объясняющих переменных некорректно, т. к.  , это означает, что разность
, это означает, что разность  незначительна и можно сделать вывод о целесообразности одновременного отбрасывания k факторов, поскольку это не привело к существенному ухудшению общего качества уравнения регрессии. Тогда нуль-гипотеза не может быть отброшена.
незначительна и можно сделать вывод о целесообразности одновременного отбрасывания k факторов, поскольку это не привело к существенному ухудшению общего качества уравнения регрессии. Тогда нуль-гипотеза не может быть отброшена.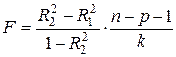 . (32)
. (32) всегда растет при добавлении новой переменной, а в скорректированном
всегда растет при добавлении новой переменной, а в скорректированном  . (33)
. (33) , (34)
, (34) – стандартизованные коэффициенты регрессии,
– стандартизованные коэффициенты регрессии,  – парные коэффициенты корреляции результата с каждым из факторов.
– парные коэффициенты корреляции результата с каждым из факторов. , (35)
, (35) (36)
(36) (37)
(37) , для зависимости
, для зависимости  может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. . Тогда можно говорить, что параметр b1 измеряет силу влияния фактора х1 на результат у при неизменном значении фактора х2. Если же
. Тогда можно говорить, что параметр b1 измеряет силу влияния фактора х1 на результат у при неизменном значении фактора х2. Если же  , то с изменением фактора х1 фактор х2 не может оставаться неизменным. Отсюда b1 и b2 нельзя интерпретировать как показатель раздельного влияния х1 и х2 на у.
, то с изменением фактора х1 фактор х2 не может оставаться неизменным. Отсюда b1 и b2 нельзя интерпретировать как показатель раздельного влияния х1 и х2 на у.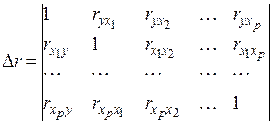 (38)
(38) .
. матрица парных коэффициентов корреляции оказалась следующей:
матрица парных коэффициентов корреляции оказалась следующей: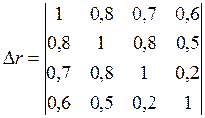 .
. ). Однако в модель следует включить фактор х2, а не х1, поскольку корреляция фактора х2 с у достаточно высокая (
). Однако в модель следует включить фактор х2, а не х1, поскольку корреляция фактора х2 с у достаточно высокая ( ), а с фактором х3 слабая (
), а с фактором х3 слабая ( ).
). .
. имеет приближенное распределение χ2 с
имеет приближенное распределение χ2 с  степенями свободы.
степенями свободы. , то гипотеза Н 0 отклоняется, мультиколлинеарность считается доказанной.
, то гипотеза Н 0 отклоняется, мультиколлинеарность считается доказанной. рассчитывается по следующей регрессии:
рассчитывается по следующей регрессии:
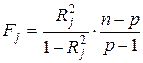 . (39)
. (39) статистически значим, то
статистически значим, то  . В этом случае
. В этом случае 
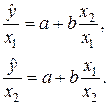 (40)
(40) , (41)
, (41) .
. после исключения влияния
после исключения влияния  определяется по следующему алгоритму:
определяется по следующему алгоритму: .
.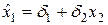 .
. и
и  .
. :
: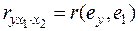 . (42)
. (42) , как у обычных коэффициентов корреляции. Равенство
, как у обычных коэффициентов корреляции. Равенство  нулю означает отсутствие линейного влияния переменной
нулю означает отсутствие линейного влияния переменной 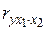 и коэффициентом детерминации
и коэффициентом детерминации 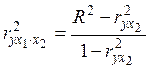 , (43)
, (43) – обычный коэффициент корреляции.
– обычный коэффициент корреляции. , сохраняя определение (42) (при этом можно в число исключаемых переменных вводить и у, определяя частную корреляцию между факторами).
, сохраняя определение (42) (при этом можно в число исключаемых переменных вводить и у, определяя частную корреляцию между факторами). (44)
(44)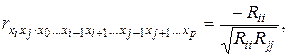 (45)
(45) – алгебраическое дополнение для элемента
– алгебраическое дополнение для элемента 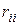 в определителе (44).
в определителе (44). – коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты более высоких порядков можно определить через коэффициенты более низких порядков по рекуррентной формуле:
– коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты более высоких порядков можно определить через коэффициенты более низких порядков по рекуррентной формуле: . (46)
. (46) (47)
(47) , а не n.
, а не n.



