Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка параметров линейной регрессииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линейная регрессия сводится к нахождению уравнения вида:
Рис. 2.1. График линии регрессии Первое выражение позволяет по заданным значениям фактора x рассчитать теоретические значения результативного признака, подставляя в него фактические значения фактора x. На графике теоретические значения лежат на прямой, которые представляют собой линию регрессии (рис. 2.1). Построение линейной регрессии сводится к оценке ее параметров а и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений
Для нахождения минимума надо вычислить частные производные суммы (4) по каждому из параметров – а и b – и приравнять их к нулю.
Преобразуем, получаем систему нормальных уравнений:
В этой системе n - объем выборки, суммы легко рассчитываются из исходных данных. Решаем систему относительно а и b, получаем:
Выражение (7) можно записать в другом виде:
где Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение парной регрессии достаточно распространенным в эконометрических исследованиях. Формально a – значение y при x = 0. Если x не имеет и не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать его могут привести к абсурду, особенно при a < 0. Интерпретировать можно лишь знак при параметре a. Если a > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Сравним эти относительные изменения:
Иногда линейное уравнение парной регрессии записывают для отклонений от средних значений:
где
Рассмотрим в качестве примера по группе предприятий, выпускающих один вид продукции, регрессионную зависимость издержек от выпуска продукции Таблица 2.1
Продолжение таблицы 2.1
Система нормальных уравнений будет иметь вид:
Решая её, получаем a = -5,79, b = 36,84.
Уравнение регрессии имеет вид:
Подставив в уравнение значения х, найдем теоретические значения y (последняя колонка таблицы). Величина a не имеет экономического смысла. Если переменные x и y выразить через отклонения от средних уровней, то линия регрессии на графике пройдет через начало координат. Оценка коэффициента регрессии при этом не изменится:
При линейной регрессии в качестве показателя тесноты связи выступает линейный коэффициент корреляции r:
Его значения находятся в границах: Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации как квадрат линейного коэффициента корреляции r2. Он характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака:
Величина
2.3. Предпосылки МНК (условия Гаусса-Маркова) Связь между y и x в парной регрессии является не функциональной, а корреляционной. Поэтому оценки параметров a и b являются случайными величинами, свойства которых существенно зависят от свойств случайной составляющей ε. Для получения по МНК наилучших результатов необходимо выполнение следующих предпосылок относительно случайного отклонения (условия Гаусса-Маркова):
1. Математическое ожидание случайного отклонения равно нулю для всех наблюдений: 2. Дисперсия случайных отклонений постоянна: Выполнимость данной предпосылки называется гомоскедастичностью -постоянством дисперсии отклонений. Невыполнимость данной предпосылки называется гетероскедастичностью -непостоянством дисперсии отклонений. 3. Случайные отклонения εi и εj являются независимыми друг от друга для
Выполнимость этого условия называется отсутствием автокорреляции. 4. Случайное отклонение должно быть независимо от объясняющих переменных. Обычно это условие выполняется автоматически, если объясняющие переменные в данной модели не являются случайными. Кроме того, выполнимость данной предпосылки для эконометрических моделей не столь критична по сравнению с первыми тремя. При выполнимости указанных предпосылок имеет место теорема Гаусса-Маркова: оценки (7) и (8), полученные по МНК, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок. Таким образом, при выполнении условий Гаусса - Маркова оценки (7) и (8) являются не только несмещенными оценками коэффициентов регрессии, но и наиболее эффективными, т. е. имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин yi. Именно понимание важности условий Гаусса - Маркова отличает компетентного исследователя, использующего регрессионный анализ, от некомпетентного. Если эти условия не выполнены, исследователь должен это сознавать. Если корректирующие действия возможны, то аналитик должен быть в состоянии их выполнить. Если ситуацию исправить невозможно, исследователь должен быть способен оценить, насколько серьезно это может повлиять на результаты. 2.4. Оценка существенности параметров линейной После того, как найдено уравнение линейной регрессии (3), проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии в целом дается с помощью F -критерия Фишера. При этом выдвигается нулевая гипотеза Перед расчетом критерия проводятся анализ дисперсии. Можно показать, что общая сумма квадратов отклонений (СКО) y от среднего значения
(Общая СКО) =
Здесь возможны два крайних случая: когда общая СКО в точности равна остаточной и когда общая СКО равна факторной. В первом случае фактор х не оказывает влияния на результат, вся дисперсия y обусловлена воздействием прочих факторов, линия регрессии параллельна оси Ох и Во втором случае прочие факторы не влияют на результат, y связан с x функционально, и остаточная СКО равна нулю. Но на практике в правой части (13) присутствуют оба слагаемых. Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации y приходится на объясненную вариацию. Если объясненная СКО будет больше остаточной СКО, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат y. Это равносильно тому, что коэффициент детерминации будет приближаться к единице.
Число степеней свободы. (df-degrees of freedom) - это число независимо варьируемых значений признака. Для общей СКО требуется Факторную СКО можно выразить так:
Эта СКО зависит только от одного параметра b, поскольку выражение под знаком суммы к значениям результативного признака не относится. Следовательно, факторная СКО имеет одну степень свободы, и Для определения
Таким образом, можем записать Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы:
Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим F -критерий для проверки нулевой гипотезы, которая в данном случае записывается как
Если Английским статистиком Снедекором разработаны таблицы критических значений F при разных уровнях существенности Снедекором и различных числах степеней свободы. Табличное значение F -критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. При нахождении табличного значения F -критерия задается уровень значимости (обычно 0,05 или 0,01) и две степени свободы – числителя (она равна единице) и знаменателя, равная Вычисленное значение F признается достоверным (отличным от единицы), если оно больше табличного, т. е. Если Величина F -критерия связана с коэффициентом детерминации.
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.
Стандартная ошибка коэффициента регрессии определяется по формуле:
Величина стандартной ошибки совместно с t- распределением Стьюдента при Величина коэффициента регрессии сравнивается с его стандартной ошибкой; определяется фактическое значение t- критерия Стьюдента
которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы Если
Существует связь между
Отсюда следует, что
. Доверительный интервал для b определяется как
где
Стандартная ошибка параметра
Процедура оценивания существенности a не отличается от таковой для параметра b. При этом фактическое значение t -критерия вычисляется по формуле:
Процедура проверки значимости линейного коэффициента корреляции отличается от процедур, приведенных выше. Это объясняется тем, что r как случайная величина распределена по нормальному закону лишь при большом числе наблюдений и малых значениях | r |. В этом случае гипотеза об отсутствии корреляционной связи между y и х
которая при справедливости Но при малых выборках и значениях r, близких к Чтобы обойти это затруднение, используется так называемое
которое дает нормально распределенную величину z, значения которой при изменении r от –1 до +1 изменяются от -∞ до +∞. Стандартная ошибка этой величины равна:
Для величины z имеются таблицы, в которых приведены её значения для соответствующих значений r. Для z выдвигается нуль-гипотеза
которая распределена по закону Стьюдента с ( Для каждого значения z можно вычислить критические значения r. Таблицы критических значений r разработаны для уровней значимости 0,05 и 0,01 и соответствующего числа степеней свободы. Если вычисленное значение r превышает по абсолютной величине табличное, то данное значение r считается существенным. В противном случае фактическое значение несущественно. 2.5. Нелинейные модели регрессии До сих пор мы рассматривали лишь линейную модель регрессионной зависимости y от x (3). В то же время многие важные связи в экономике являются нелинейными. Примерами такого рода регрессионных моделей являются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т. п.) и функции спроса (зависимости между спросом на какой-либо вид товаров или услуг, с одной стороны, и доходом и ценами на этот и другие товары – с другой). При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации. В случае линеаризации нелинейной зависимости получаем линейное регрессионное уравнение типа (3), параметры которого оцениваются обычным МНК, после чего можно записать исходное нелинейное соотношение. Несколько особняком в этом смысле стоит полиномиальная модель произвольной степени:
к которой обычный МНК можно применять без всякой предварительной линеаризации. Рассмотрим указанную процедуру применительно к параболе второй степени:
Такая зависимость целесообразна в случае, если для некоторого интервала значений фактора возрастающая зависимость меняется на убывающую или наоборот. В этом случае можно определить значение фактора, при котором достигается максимальное или минимальное значение результативного признака. Если исходные данные не обнаруживают изменение направленности связи, параметры параболы становятся трудно интерпретируемыми, и форму связи лучше заменить другими нелинейными моделями. Применение МНК для оценки параметров параболы второй степени сводится к дифференцированию суммы квадратов остатков регрессии по каждому из оцениваемых параметров и приравниванию полученных выражений нулю. Получается система нормальных уравнений, число которых равно числу оцениваемых параметров, т. е. трем:
Решать эту систему можно любым способом, в частности, методом определителей. Экстремальное значение функции наблюдается при значении фактора, равном:
Если В нелинейных зависимостях, неявляющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей. Зависимости гиперболического типа имеют вид:
Примером такой зависимости является кривая Филлипса, констатирующая обратную зависимость процента прироста заработной платы от уровня безработицы. В этом случае значение параметра b будет больше нуля. Другим примером зависимости (33) являются кривые Энгеля, формулирующие следующую закономерность: с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается, а доля доходов, расходуемых на непродовольственные товары, будет возрастать. В этом случае Линеаризация уравнения (33) сводится к замене фактора
К такому же линейному уравнению сводится полулогарифмическая кривая:
которая может быть использована для описания кривых Энгеля. Здесь ln(x) заменяется на z и получается уравнение (34). Достаточно широкий класс экономических показателей характеризуется приблизительно постоянным темпом относительного прироста во времени. Этому соответствуют зависимости показательного (экспоненциального) типа, которые записываются в виде:
или в виде
Возможна и такая зависимость:
В регрессиях типа (36) – (38) применяется один и тот же способ линеаризации – логарифмирование. Уравнение (36) приводится к виду:
Замена переменной
где
который отличается от (39) только видом свободного члена, и линейное уравнение выглядит так:
где
где Широко распространены в практике социально-экономических исследований степенные зависимости. Они используются для построения и анализа производственных функций. В функциях вида:
особенно ценным является то обстоятельство, что параметр b равен коэффициенту эластичности результативного признака по фактору х. Преобразуя (44) путем логарифмирования, получаем линейную регрессию:
где Еще одним видом нелинейности, приводимым к линейному виду, является обратная зависимость:
Проводя замену
Наконец, следует отметить зависимость логистического типа:
Графиком функции (48) является так называемая «кривая насыщения», которая имеет две горизонтальные асимптоты
Рис. 2.2. Кривая насыщения
Уравнение (48) приводится к линейному виду заменами переменных Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:
Здесь Следует обратить внимание на то, что разности в соответствующих суммах
Величина R находится в границах Так обстоит дело с полулогарифмической и полиномиальной регрессией, а также с равносторонней гиперболой (33). Определив линейный коэффициент корреляции для линеаризованных уравнений, например, в пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и для нелинейной зависимости. Иначе обстоит дело в случае, когда преобразование проводится также с величиной y, например, взятие обратной величины или логарифмирование. Тогда значение R, вычисленное той же функцией ЛИНЕЙН, будет относиться к линеаризованному уравнению регрессии, а не к исходному нелинейному уравнению, и величины разностей под суммами в (50) будут относиться к преобразованным величинам, а не к исходным, что не одно и то же. При этом, как было сказано выше, для расчета R следует воспользоваться выражением (50), вычисленным по исходному нелинейному уравнению. Поскольку в расчете индекса корреляции используется соотношение факторной и общей СКО, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации. Оценка существенности индекса корреляции проводится так же, как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F -критерию Фишера:
где n - число наблюдений, m - число параметров при переменных х. Во всех рассмотренных нами случаях, кроме полиномиальной регрессии,
Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем больше разница между R2 и r2. Близость этих показателей означает, что усложнять форму уравнения регрессии не следует и можно использовать линейную функцию. Практически, если величина
Здесь в знаменателе находится ошибка разности
Если В заключение в таблице 2.2 приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии. Таблица 2.2
Контрольные вопросы 1. В чем состоит суть метода наименьших квадратов? 2. В каком случае остаточная сумма квадратов равна нулю? 3. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное… 4. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное… 5. На чем основан классический метод к оцениванию параметров регрессии? 6. Какое уравнение регрессии нельзя свести к линейному виду: a) b) c) 7. Какие значения может принимать коэффициент корреляции 8. Какое из следующих уравнений нелинейно по оцениваемым параметрам: a) b) c) 9. Для функции a) b) c)
3. ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

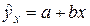 (или
(или 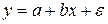 ).
).
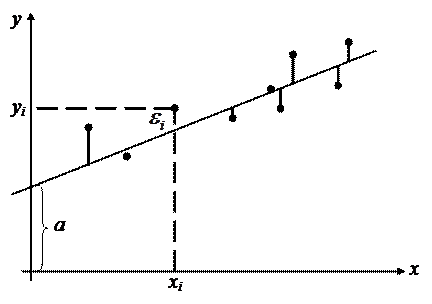
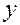 от теоретических
от теоретических  минимальна:
минимальна: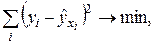 или
или 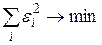 .
.
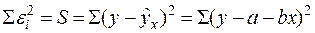
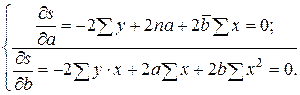 (5)
(5)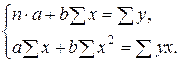 (6)
(6) (7)
(7)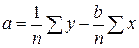 . (8)
. (8)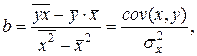 (9)
(9)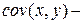 ковариация признаков,
ковариация признаков, 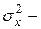 дисперсия фактора x.
дисперсия фактора x. <
<  при
при 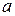 > 0,
> 0,  > 0
> 0  <
< 



 , (10)
, (10) ,
,  . При этом свободный член равен нулю, что и отражено в выражении (10). Этот факт следует из геометрических соображений: уравнению регрессии отвечает та же прямая (3), но при оценке регрессии в отклонениях начало координат перемещается в точку с координатами
. При этом свободный член равен нулю, что и отражено в выражении (10). Этот факт следует из геометрических соображений: уравнению регрессии отвечает та же прямая (3), но при оценке регрессии в отклонениях начало координат перемещается в точку с координатами  . При этом в выражении (8) обе суммы будут равны нулю, что и повлечет равенство нулю свободного члена.
. При этом в выражении (8) обе суммы будут равны нулю, что и повлечет равенство нулю свободного члена. .
. )
)





 .
. , где
, где  .
.
 . Если b > 0, то
. Если b > 0, то  при b < 0:
при b < 0:  .
. .
.
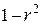 характеризует долю дисперсии y, вызванную влиянием остальных, не учтенных в модели факторов.
характеризует долю дисперсии y, вызванную влиянием остальных, не учтенных в модели факторов.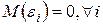 .
. .
.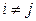 :
:
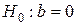 о том, что коэффициент регрессии равен нулю и, следовательно, фактор х не оказывает влияния на результат y.
о том, что коэффициент регрессии равен нулю и, следовательно, фактор х не оказывает влияния на результат y.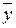 раскладывается на две части – объясненную и необъясненную:
раскладывается на две части – объясненную и необъясненную: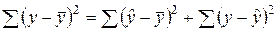 (13)
(13)

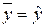 .
.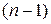 независимых отклонений, т. к.
независимых отклонений, т. к. 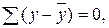 что позволяет свободно варьировать
что позволяет свободно варьировать  .
.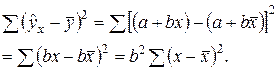
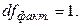
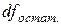 воспользуемся аналогией с балансовым равенством (11). Так же, как и в равенстве (11), можно записать равенство и между числами степеней свободы:
воспользуемся аналогией с балансовым равенством (11). Так же, как и в равенстве (11), можно записать равенство и между числами степеней свободы: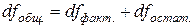 (14)
(14)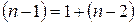 . Из этого баланса определяем, что
. Из этого баланса определяем, что 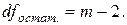
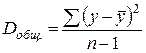 . (15)
. (15)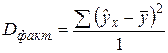 . (16)
. (16)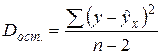 . (17)
. (17)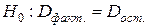
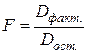 (18)
(18)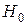 справедлива, то дисперсии не отличаются друг от друга. Для
справедлива, то дисперсии не отличаются друг от друга. Для 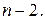
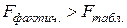 (α;1;
(α;1; 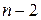 ). В этом случае
). В этом случае 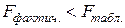 , то вероятность
, то вероятность 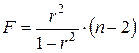 , (19)
, (19)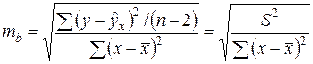 , (20)
, (20)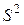 - остаточная дисперсия на одну степень свободы (то же, что и
- остаточная дисперсия на одну степень свободы (то же, что и 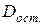 ).
).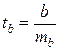 , (21)
, (21)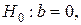 также предполагающая несущественность статистической связи между y и х, но только учитывающая значение b, а не соотношение между факторной и остаточной дисперсиями в общем балансе дисперсии результативного признака. Но общий смысл гипотез один и тот же: проверка наличия статистической связи между y и х или её отсутствия.
также предполагающая несущественность статистической связи между y и х, но только учитывающая значение b, а не соотношение между факторной и остаточной дисперсиями в общем балансе дисперсии результативного признака. Но общий смысл гипотез один и тот же: проверка наличия статистической связи между y и х или её отсутствия.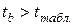 (α;
(α; 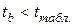 (α;
(α; 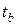 и F:
и F: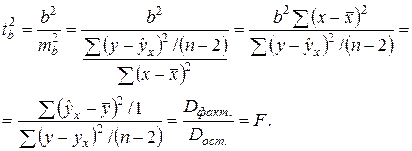
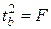 . (22)
. (22)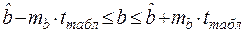 (23)
(23)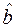 – рассчитанное (оцененное) по МНК значение коэффициента регрессии.
– рассчитанное (оцененное) по МНК значение коэффициента регрессии.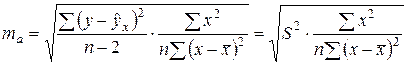 . (24)
. (24)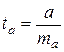 . (25)
. (25)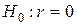 проверяется на основе статистики
проверяется на основе статистики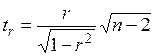 , (26)
, (26)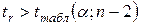 , то гипотеза
, то гипотеза 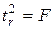 . Кроме того,
. Кроме того, 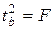 , поэтому
, поэтому 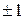 , следует учитывать, что распределение r как случайной величины отличается от нормального, и построение доверительных интервалов для r не может быть выполнено стандартным способом. В этом случае вообще легко прийти к противоречию, заключающемуся в том, что доверительный интервал будет содержать значения, превышающие единицу.
, следует учитывать, что распределение r как случайной величины отличается от нормального, и построение доверительных интервалов для r не может быть выполнено стандартным способом. В этом случае вообще легко прийти к противоречию, заключающемуся в том, что доверительный интервал будет содержать значения, превышающие единицу. , (27)
, (27) . (28)
. (28)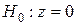 , состоящая в том, что корреляция отсутствует. В этом случае значения статистики
, состоящая в том, что корреляция отсутствует. В этом случае значения статистики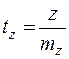 , (29)
, (29)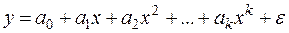 , (30)
, (30) . (31)
. (31)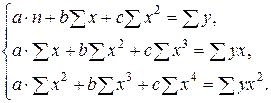 (32)
(32)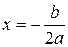 .
.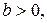
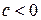 , то имеет место максимум, т. е. зависимость сначала растет, а затем падает. Такого рода зависимости наблюдаются в экономике труда при изучении заработной платы работников физического труда, когда в роли фактора выступает возраст. При
, то имеет место максимум, т. е. зависимость сначала растет, а затем падает. Такого рода зависимости наблюдаются в экономике труда при изучении заработной платы работников физического труда, когда в роли фактора выступает возраст. При 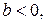
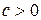 парабола имеет минимум, что обычно проявляется в удельных затратах на производство в зависимости от объема выпускаемой продукции.
парабола имеет минимум, что обычно проявляется в удельных затратах на производство в зависимости от объема выпускаемой продукции.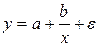 . (33)
. (33)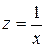 , и уравнение регрессии имеет вид (3), в котором вместо фактора х используем фактор z:
, и уравнение регрессии имеет вид (3), в котором вместо фактора х используем фактор z: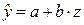 . (34)
. (34)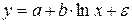 , (35)
, (35)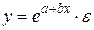 (36)
(36)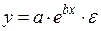 . (37)
. (37)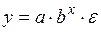 . (38)
. (38)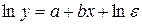 . (39)
. (39)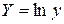 сводит его к линейному виду:
сводит его к линейному виду: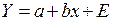 , (40)
, (40) . Если Е удовлетворяет условиям Гаусса-Маркова, параметры уравнения (36) оцениваются по МНК из уравнения (40). Уравнение (37) приводится к виду:
. Если Е удовлетворяет условиям Гаусса-Маркова, параметры уравнения (36) оцениваются по МНК из уравнения (40). Уравнение (37) приводится к виду: , (41)
, (41)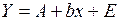 , (42)
, (42) . Параметры А и b получаются обычным МНК, затем параметр a в зависимости (37) получается как антилогарифм А. При логарифмировании (38) получаем линейную зависимость:
. Параметры А и b получаются обычным МНК, затем параметр a в зависимости (37) получается как антилогарифм А. При логарифмировании (38) получаем линейную зависимость: , (43)
, (43)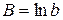 , а остальные обозначения те же, что и выше. Здесь также применяется МНК к преобразованным данным, а параметр b для (38) получается как антилогарифм коэффициента В.
, а остальные обозначения те же, что и выше. Здесь также применяется МНК к преобразованным данным, а параметр b для (38) получается как антилогарифм коэффициента В.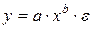 (44)
(44)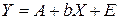 , (45)
, (45)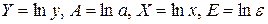 .
.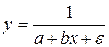 . (46)
. (46)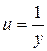 , получим:
, получим: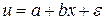 . (47)
. (47)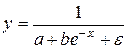 . (48)
. (48)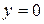 ,
,  и точку перегиба
и точку перегиба 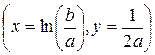 , а также точку пересечения с осью ординат
, а также точку пересечения с осью ординат 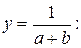

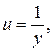
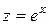 .
.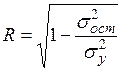 (49)
(49)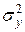 - общая дисперсия результативного признака y,
- общая дисперсия результативного признака y, 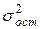 - остаточная дисперсия, определяемая по уравнению нелинейной регрессии
- остаточная дисперсия, определяемая по уравнению нелинейной регрессии 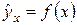 .
.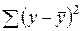 и
и 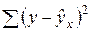 берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. Индекс корреляции (49) можно записать так:
берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. Индекс корреляции (49) можно записать так: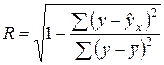 (50)
(50)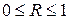 и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с линейным коэффициентом корреляции в случае, когда преобразование переменных с целью линеаризации уравнения регрессии не проводится с величинами результативного признака.
и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с линейным коэффициентом корреляции в случае, когда преобразование переменных с целью линеаризации уравнения регрессии не проводится с величинами результативного признака.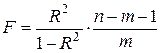 , (51)
, (51)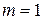 , для полиномов (30)
, для полиномов (30) 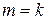 , т. е. степени полинома. Величина m характеризует число степеней свободы для факторной СКО, а
, т. е. степени полинома. Величина m характеризует число степеней свободы для факторной СКО, а 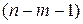 – число степеней свободы для остаточной СКО.
– число степеней свободы для остаточной СКО. не превышает 0,1, то линейная зависимость считается оправданной. В противном случае проводится оценка существенности различия показателей детерминации, вычисленных по одним и тем же данным, через t -критерий Стьюдента:
не превышает 0,1, то линейная зависимость считается оправданной. В противном случае проводится оценка существенности различия показателей детерминации, вычисленных по одним и тем же данным, через t -критерий Стьюдента: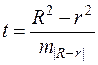 . (52)
. (52)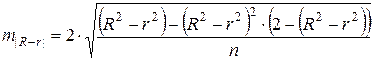 . (53)
. (53) , то различия между показателями корреляции существенны и замена нелинейной регрессии линейной нецелесообразна.
, то различия между показателями корреляции существенны и замена нелинейной регрессии линейной нецелесообразна.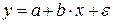
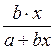
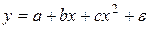
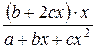
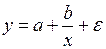
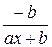
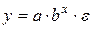
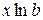
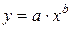
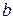
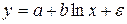
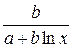

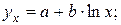
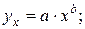
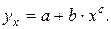
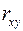 ?
?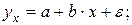
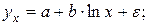
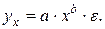
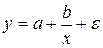 средний коэффициент эластичности имеет вид:
средний коэффициент эластичности имеет вид: