
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод наименьших квадратов (МНК) в расчете уравнения регрессииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы. Студент должен знать: смысл регрессии x по y (регрессионных зависимостей), способы определения параметров регрессии (для линейной и квадратичной регрессии), метод наименьших квадратов. Студент должен уметь: произвести расчет уравнения регрессии по результатам экспериментов произвести анализ программ ЭВМ для реализации метода регрессионного анализа. Практическое значение выполняемых исследований Различные величины, наблюдаемые в эксперименте, могут явно или неявно зависеть друг от друга. В последнем случае мы говорим о регрессии y по x Использование программ в языках программирования (например, BASIC) для нахождения параметров уравнения регрессии и обработки результатов экологических исследований. Данная работа позволяет обучаемому получить необходимые навыки в этой области. Литература 1. В.М. Еськов, О.Е. Филатова, В.А. Рачковская Статистическая обработка результатов измерений в практикуме по экологии и естествознанию.- Сургут: Изд. СурГУ, 1999.- 43 с. 2. М. Дж. Кендалл, А. Стьюарт. Теория распределений. 3. В. В. Гмурман. Теория вероятностей и математическая статистика. – М.: 4. Ю. В. Линник. Метод наименьших квадратов. – М. – 2001. – 196 с. Бюджет времени На изучение темы отводится 6 часов, из них 2 часа лекций, 2 часа лабораторные занятия и 2 часа на самоподготовку.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ "Самоподготовка" Для подготовки к лабораторной работе Вам следует повторить пройденный материал и изучить лекции. Ответьте на следующие вопросы: 1. Что такое регрессионное уравнение? Для чего его используют? 2. Как проверяется соответствие гипотезы эксперименту методом наименьших квадратов? 3. Приведите алгоритм нахождения линейной регрессии.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО II ЭТАПУ: “Выполнение лабораторной работы” Для выполнения этапа наберите описанную в блоке информации программу, реализующую алгоритм нахождения регрессионных уравнений. Оцените полученные параметры уравнения регрессии и сделайте выводы. Блок информации Сглаживание экспериментальных зависимостей можно выполнять методом наименьших квадратов. Уравнение регрессии может быть линейным, квадратичным и др. Рассмотрим простейший случай зависимости y=kx+b. Часто требуется построение графиков по эмпирическим данным или экспериментальное подтверждение известным из теории функциональным зависимостям между физическими величинами. Например, известна зависимость сопротивления металлов от температуры
которую можно записать в виде линейной зависимости y=ax+b, (10.2) где у=Rt, x=t, b=Ro, a=Roa. Часто популяционный рост на небольших участках времени также аппроксимирует такой линейной зависимосьтью. В общем случае экспериментальных измерениях получают множество xi и соответствующих им yi (в данном случае ti и Rti). Однако, существуют случайные отклонения (ошибки) и, как следствие, разброс точек, т.е. вместо гладкой линии получается ломаная кривая. Для усреднения эмпирических зависимостей и получения наиболее реального графика используют графический, арифметический, алгебраический способы выравнивания экспериментальных данных. Наиболее точный из них- алгебраический, метод наименьших квадратов. В этом случае составляют сумму квадратов отклонений эмпирических значений yi от предполагаемых теоретических f(xi) и требуют минимума этой суммы, т.е.
где W®min, n- число измерений При этом отдельные точки могут значительно отклоняться от графика (см. рис. 10.1), но, в целом, вся совокупность точек отклоняется на минимальное расстояние. Так как в функцию f(x) входят параметры a,b,.., т.е. f(x,a,b...), то минимизируют по параметрам, используя необходимое условие экстремума функции W=W(a, b):
Поясним выше сказанное на конкретном примере зависимости (10.2). Здесь после подстановки f(x) имеем:
тогда
или
а
или
Получим систему двух уравнений (10.5)и (10.6) относительно неизвестных a и b (yi,xi получены в эксперименте). Эта система имеет вид:
Рис.10.1. Реализация метода наименьших квадратов
где
Тогда получим
Из решения этой системы уравнений можно получить для примера (10.1) значения параметров R0 и a:
и температурный коэффициент
Зная Ro и a легко построить график зависимости R=R(t). Отметим, что зависимость среднего значения какой- либо величины (например, R) от некоторой другой величины (t) называется регрессией y=u(х). Уравнение y=u(х), в котором х играет роль "независимой" переменной называется уравнением регрессии, а соответствующий график- линией регрессии величины у по х. Если регрессия у по х линейная, то можно записать, что
где my mx- математическое ожидание х и у, sx2 sy2- дисперсии х и у, r- коэффициент корреляции между х и у. Существенно, что для нормального совместного распределения обе линии регрессии y=u(х) и х=v(у) являются прямыми. Понятие коэффициента корреляции r раскрывается в следующей работе.
Приложение 1
ПРОГРАММА ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ РЕГРЕССИИ
REM ************ f(x)=kx+b ******************** CLS INPUT "введите количество n: ", n DIM x(n): DIM y(n) REM ********* заполнение массивов ************* FOR i = 1 TO n PRINT "x ("; i; ") =";: INPUT "", x(i) PRINT "y ("; i; ") =";: INPUT "", y(i) NEXT i REM ******************************************* REM******************************************** FOR i = 1 TO n L = L - x(i) * y(i): REM L=S(-yx) M = M + x(i) * x(i): REM M=S(x¤) NN = NN + x(i): REM NN=S(x) R = R + y(i): REM R=S(y) NEXT i REM ******************************************* REM******************************************** k = (L * n + R * NN) / (NN ^ 2 - M * n) b = (R - k * NN) / n PRINT "Имеем зависимость вида: y = k * x + b, где" PRINT "k = "; k PRINT "b = "; b
Лабораторная работа № 11 Программа расчета уравнения регрессии и коэффициента корреляции
Блок информации Понятия о корреляционных зависимостях. Вычисление коэффициента корреляции. Множественная корреляция. Существуют методы оценки близости полученных эмпирических данных с функциональными зависимостями типа (3.10), более того, можно оценить степень взаимосвязи различных наблюдаемых переменных, используя коэффициент корреляции r. Отметим, что в корреляционном анализе уравнение (3.10) получило название выборочного уравнения прямой линии регрессии у на х, причем, коэффициент a=ryx получил название выборочного коэффициента регрессии у на х. При большом числе измерений каждому из значений х и у соответствует не одно, а несколько значений этих величин. Тогда данные эксперимента группируют в так называемую корреляционную таблицу (см. таблицу 2). В этой таблице nv - число встречаемости одинаковых значений v, а nt - одинаковых t и nvt - число встречаемости одинаковых пар v и t во всех опытах (они находятся на пересечении соответствующих строк и столбцов). В первой строке таблицы указаны наблюдаемые значения СВ t, а в первом столбце - значения СВ v. Очевидно, что
т.е. общему числу измерений. Отметим, что средние значения
Тогда коэффициент регрессии определится по формуле, которая является модификацией (3.15) с учетом замечаний (3.17).
Выборочный коэффициент корреляции
Как уже отмечалось выше (2.IV) для распределения Гаусса при r=0 величины v и t независимы, а при r=1 они связаны чисто функциональной зависимостью типа (3.10), что весьма важно для практических выводов. В данном примере (таблица 2) зависимость v=vo+rvtt имеет конкретный физический смысл- это газовый закон Гей-Люссака, причем В общем случае выборочный коэффициент корреляции определяется по формуле:
где
Существенно, что r может отличаться от коэффициента корреляции rх,у, который можно рассчитать по формуле:
где При изучении связи между несколькими СВ х1, х2, …, хn используют корреляционную матрицу, состоящую из коэффициентов корреляции rij. Используют также множественный коэффициент корреляции. Например, при n=3 имеем
который характеризует меру линейной зависимости между СВ х1 2-мя другими СВ (х2 и х3). Для таких случаев вычисляются и частные коэффициенты корреляции (когда, например, исключается влияние х3) между х1 и х2. Для этих величин разработаны специальные программы на ЭВМ.
Приложение 1 ПРОГРАММА РАССЧЕТА КОЭФФИЦИЕНТОВ КОРРЕЛЛЯЦИИ
REM **программа вычисляет коэффициент корреляции ** CLS xs = 0: ys = 0: h = 0: sdx = 0: sdy = 0 INPUT "Kоличество n= ", n REM ********* заполнение массивов *********** DIM x(n): DIM y(n) FOR m = 1 TO n PRINT "x ("; m; ") =";: INPUT "", x(m) PRINT "y ("; m; ") =";: INPUT "", y(m) NEXT m REM ******************************************** REM ************* средние x и y ****************** FOR m = 1 TO n xs = xs + x(m) ys = ys + y(m) NEXT m xs = xs / n: ys = ys / n REM ******************************************* FOR m = 1 TO n: sdx = sdx + (x(m) - xs): NEXT m FOR m = 1 TO n: sdy = sdy + (y(m) - ys): NEXT m FOR m = 1 TO n: h = h + (y(m) - ys) * (x(m) - xs): NEXT m REM ******************************************** REM ************ дисперсия ********************* FOR m = 1 TO n sx = sx + (x(m) - xs) ^ 2 sy = sy + (y(m) - ys) ^ 2 NEXT m cx = sdx / n: cy = sdy / n REM **** среднее квадратическое отклонение ***** sxs = SQR((sx / n) - cx ^ 2) sys = SQR((sy / n) - cy ^ 2) REM ********* коэффициент корреляции *********** rxy = ((h / n) - cx * cy) / (sxs * sys) PRINT "Koэффициeнт kоppеляции rxy= "; rxy SLEEP 15
Лабораторная работа № 12.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.007 с.) |

 (10.1)
(10.1) (10.3)
(10.3) (10.4)
(10.4) ,
,
 (10.5)
(10.5)
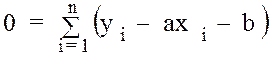 (10.6)
(10.6)

 .
.
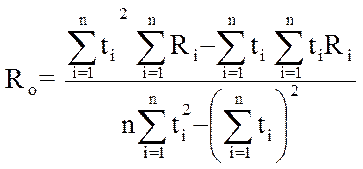 (10.7)
(10.7) (10.8)
(10.8)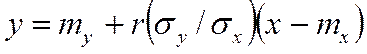 ,
, ,
, , (3.17)
, (3.17) (3.18)
(3.18) , где
, где  и
и  - выборочные средние квадратические отклонения, определяемые по формулам
- выборочные средние квадратические отклонения, определяемые по формулам (3.19)
(3.19)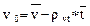 , а из rvt можно найти a - коэффициент теплового расширения газа (rvt=voa).
, а из rvt можно найти a - коэффициент теплового расширения газа (rvt=voa). ,
,
 ,
, , а sх и sу- средние квадратические отклонения.
, а sх и sу- средние квадратические отклонения. ,
,


