
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет доверительного интервала на эвмСодержание книги Поиск на нашем сайте
Цель работы. Студент должен знать: смысл первичной статистической обработки результатов исследований до доверительного интервала с погрешностью измерений, правило 3-х сигм для случайных величин. Студент должен уметь: произвести первичную статистическую обработку результатов экологических экспериментов до x±dx, произвести определение величины (размеров) конкретного биообъекта (среднее значение, выше среднего, высокий).
Практическое значение выполняемых исследований С использованием методов математической статистики можно давать оценку любого биообъекта. Может быть выполнен анализ основных погрешностей в различных измерениях с использованием критерия Стьюдента. Использование программ в языках программирования (например, BASIC) для нахождения доверительного интервала и обработки результатов позволяет резко облегчить механические многократно повторяемые операции в расчетах и повысить их точность. Литература 1. В.М. Еськов, О.Е. Филатова, В.А. Рачковская Статистическая обработка результатов измерений в практикуме по экологии и естествознанию.- Сургут: Изд. СурГУ, 1999.- 43 с. 2. М. Дж. Кендалл, А. Стьюарт. Теория распределений. 3. В. В. Гмурман. Теория вероятностей и математическая статистика.
Бюджет времени На изучение темы отводится 6 часов, из них 2 часа лекций, 2 часа лабораторные занятия и 2 часа на самоподготовку.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ "Самоподготовка" Для подготовки к лабораторной работе Вам следует повторить математику и математические методы за 1-2 курс, изучить лекции и ответить на следующие вопросы: 1. Каков смысл доверительного интервала? 2. Сформулируйте метод нахождения дисперсии и средне квадратического отклонения. 3. Для чего используется коэффициент Стьюдента? 4. Что такое дисперсия результата в экологическом смысле? 5. В чем смысл "правила трех сигм"? 6. Как перейти от доверительного интервала к стандартной форме записи
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО II ЭТАПУ: “Выполнение лабораторной работы” Для выполнения этапа наберите описанную в блоке информации программу, реализующую алгоритм нахождения доверительного интервала. Оцените результат по критериям поиска грубых ошибок (промахов) эксперимента. Если таковые присутствуют, удалите их из выборки и проведите расчет заново. Выборку используйте по данным роста и массы студентов свей группы (студенты однокурсники) или из литературы разных пород рыб, одного года (например, двухлетний язь или карп и т.д.)
Блок информации Рассмотрим первичную обработку результатов измерений до доверительного интервала. Определив в предыдущей работе №8 круг основных задач СОРЭИ и исходную информацию в области математической статистики, рассмотрим теперь конкретное применение указанного подхода при выполнении эколого-технических измерений, понимая под этим любые измерения в биологии, экологии, медицине, физике, химии, т.е. в естествознании вообще. Прежде всего отметим, что вместо вероятности события P(x) мы будем пользоваться частотой P*(x)=m/N (см. л.р. №8) и тогда все формулы ТВ можно применить с некоторой точностью, заменив P(x) на P*(x). При малом числе измерений (n<30) вместо распределения Гаусса используем распределение Стьюдента, которое внесет некоторые коррективы в формулы, приведенные ниже. Сразу отметим, что в экологии (как и в физике, технике и др. науках) могут быть прямые измерения и косвенные. Начнем рассмотрение с 1-го блока, как наиболее распространенного. I Прямые измерения. Расчет доверительного интервала. Прежде всего отметим, что общая схема (алгоритм) первичной статистической обработки результатов измерений примет следующий вид для случая прямых измерений: 1. Нахождение выборочного математического ожидания (или среднего арифметического):
2. Нахождение статистической (выборочной) дисперсии (или центрального момента 2-го порядка):
3. Определение статистического (выборочного) среднего квадратического отклонения СВ:
Если n велико, то величины
Легко видеть, что с увеличением n средняя квадратическая ошибка среднего арифметического (выборочного математического ожидания) 4. В первом случае используем правило трех сигм и определяем наиболее возможную ошибку отдельного измерения
Как известно (см. выше), вероятность непопадания СВ в интервал
1®2®3®4®5®6 (9.5)
5. Далее, точность прямого измерения Dx, т.е. разность между xo (истинным значением СВ) и ее
где tk,b - параметр, при малых n задается таблицей 1 (для критерия Стьюдента
k=n-1 (9.7)
6. Для ответа на второй вопрос мы должны записать доверительный интервал ( Важно отметить, что истинные значение СВ мы так и не определим, но получаем определенную оценку xo. Этим объясняется невозможность исключить случайные ошибки. Иногда молодые исследователи говорят, что провели несколько измерений, а результат одинаковый, вывод "нет ошибки". Это утверждение неверное, т.к. фактически такая ситуация означает, что Dx СВ меньше абсолютной погрешности прибора Dxnp, тогда нужно просто приравнять эти две величины без дополнительных расчетов, т.е. сразу 1®6. II. Косвенные измерения. Приведенные выше методы расчета применимы при работе с любым измерительным прибором в экологии и при любых прямых измерениях. Однако, во многих случаях необходимая ЭТВ получается при расчете с использованием известных функциональных зависимостей между искомой величиной и непосредственно измеряемыми x1, x2,...,xn, т.е. y=y(x1...xn). В этом случае для каждой xi, используя алгоритм 1-6, находят xi и Dxi, а затем находят среднюю квадратическую погрешность косвенного измерения y по формуле:
где ¶y/¶xi - частная производная от у по хi. Приведем простейший пример, если определяют объем цилиндра (часть ствола дерева, червь и т.д.) V=pR2h, то сначала по схеме 1-6 находят
Расчет средней квадратической ошибки среднего арифметического
точности измерения В общем случае естествоиспытатель (биоэколог) должен сам уметь составлять алгоритм расчета доверительного интервала. Конкретный пример такого алгоритма (программы) представлен в приложении 1. В данной работе Вам придется измерить параметры (масса и рост) каждого студента группы и для этих двух СВ (m и n) рассчитать доверительные интервалы. Если бы выборка была побольше, например, юношей n1>10 и девушек n2>10, то можно было бы определить доверительные интервалы для юношей и девушек и сделать вывод о наличии (или отсутствии) гендерных различий среди населения Югры. Наконец, отметим еще одно важное замечание. Если для данной выборки мы получим Доверительные интервалы можно сравнивать, но для этого лучше применять статистическую проверку гипотез (см. Лаб.р. №12, №13). Приложение 1
ПРОГРАММА РАСЧЕТА ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА REM ******************************************************* CLS j = 0: Dsp = 0: INPUT "Tkb (критерий Стьюдента) = ", Tkb INPUT "количество n = ", n DIM x(n) REM *********** заполнение массива ************************** FOR i = 1 TO n PRINT "x ("; i; ") = ";: INPUT "", x(i) NEXT i REM ******************************************************* REM ************** среднее значение x *********************** FOR i = 1 TO n j = j + x(i) NEXT i j = j / n PRINT "Среднее арифметическое значения <x> = "; j REM ******************************************************* REM *********** Статистическая дисперсия ******************** FOR i = 1 TO n Dsp = Dsp + (j - x(i)) * (j - x(i)) NEXT i Dsp = Dsp / n PRINT "Статистическая дисперсия, D = "; Dsp REM ******** Cреднее квадратичное отклонение **************** Sc = SQR(Dsp) PRINT "Среднее квадратичное отклонение x = "; Sc REM *Среднее квадратичное отклонение среднего арифметического * k = n - 1 Sxc = Sc / (SQR(k)) PRINT "Среднее квадратичное отклонение среднего арифметического ="; Sxc REM ************ доверительный интервал ******************** dx = Tkb * Sxc PRINT "доверительный интервал = ("; j - dx; ","; j + dx; ")"
Лабораторная работа №10
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.219.203 (0.007 с.) |

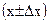 результатов эксперимента?
результатов эксперимента?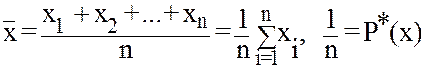 (9.1)
(9.1)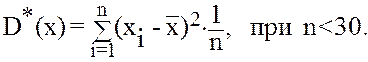 (9.2)
(9.2) (9.3)
(9.3)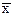 , D*(x),
, D*(x), 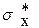 могут хорошо характеризовать истинные значения математического ожидания, дисперсии и среднего квадратического отклонения СВ (измеряемой величины). Иная ситуация возникает при небольших n (n<30, например). Вообще говоря
могут хорошо характеризовать истинные значения математического ожидания, дисперсии и среднего квадратического отклонения СВ (измеряемой величины). Иная ситуация возникает при небольших n (n<30, например). Вообще говоря  тоже является случайной величиной, как и каждая xi, поэтому оно тоже может характеризоваться средним квадратическим отклонением, которое, как показывают расчеты для распределения Стьюдента, определяется по формуле:
тоже является случайной величиной, как и каждая xi, поэтому оно тоже может характеризоваться средним квадратическим отклонением, которое, как показывают расчеты для распределения Стьюдента, определяется по формуле: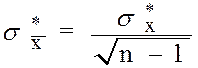 .
.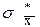 ®0. Так как нас интересует истинное значение, x0 для СВ, к которому стремится
®0. Так как нас интересует истинное значение, x0 для СВ, к которому стремится 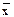 , то представляет интерес оценка точности наших измерений и ответ на вопрос, как близко
, то представляет интерес оценка точности наших измерений и ответ на вопрос, как близко 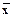 подходит к xo.
подходит к xo.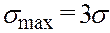 . (9.4)
. (9.4)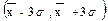 чрезвычайно мала (1-0.9972=0.0028), поэтому те значения СВ, которые не попали в этот интервал, мы должны отбросить (промахи!), а вычисления повторить заново. Тогда схема вычисления (алгоритм) примет вид:
чрезвычайно мала (1-0.9972=0.0028), поэтому те значения СВ, которые не попали в этот интервал, мы должны отбросить (промахи!), а вычисления повторить заново. Тогда схема вычисления (алгоритм) примет вид: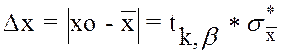 (9.6)
(9.6) ). Этот параметр можно определить из распределения Стьюдента. Он зависит от числа степеней свободы k, которое на единицу меньше числа измерений, т.е. и доверительной вероятности b.
). Этот параметр можно определить из распределения Стьюдента. Он зависит от числа степеней свободы k, которое на единицу меньше числа измерений, т.е. и доверительной вероятности b. ), внутрь которого с доверительной вероятностью b попадает неизвестное нам истинное значение xo СВ. Выбор b определяется требованиями практики. В биологических исследованиях можно брать b=0.9, т.е. из 100 случаев, в среднем, 90 раз вычисленный нами доверительный интервал накроет истинное значение СВ, а в 10 случаях - нет. Иногда предъявляют более жесткие требования (в авиации, медицине b=0.999, в космонавтике – 0,99999).
), внутрь которого с доверительной вероятностью b попадает неизвестное нам истинное значение xo СВ. Выбор b определяется требованиями практики. В биологических исследованиях можно брать b=0.9, т.е. из 100 случаев, в среднем, 90 раз вычисленный нами доверительный интервал накроет истинное значение СВ, а в 10 случаях - нет. Иногда предъявляют более жесткие требования (в авиации, медицине b=0.999, в космонавтике – 0,99999). (9.8)
(9.8)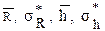 , а затем, используя (9.8)
, а затем, используя (9.8)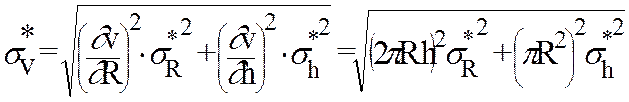 .
. ,
, и доверительного интервала (
и доверительного интервала (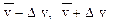 ) ничем не отличается от общей схемы 1-6.
) ничем не отличается от общей схемы 1-6. и
и 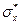 , то любой объект попавший в интервал (
, то любой объект попавший в интервал (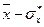 ,
, 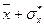 ) характеризуется как объект со средними значениями (массы, роста и т.д.). Если же его данные попали в интервал (
) характеризуется как объект со средними значениями (массы, роста и т.д.). Если же его данные попали в интервал (
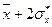 ), то мы говорим, что рост (например, h) человека ниже среднего или выше среднего. Наконец, если параметры объекта лежат за границей
), то мы говорим, что рост (например, h) человека ниже среднего или выше среднего. Наконец, если параметры объекта лежат за границей 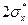 , то это или низкий (рост) или высокий (рост) показатель объекта. Так в экологии мы можем говорить о загрязненности (воды, атмосферы, почвы, крови или лимфы человека) в пределах нормы, выше (ниже) нормы (среднее) или о высоких (низких) показателях внешней для человека (или внутренней) среды.
, то это или низкий (рост) или высокий (рост) показатель объекта. Так в экологии мы можем говорить о загрязненности (воды, атмосферы, почвы, крови или лимфы человека) в пределах нормы, выше (ниже) нормы (среднее) или о высоких (низких) показателях внешней для человека (или внутренней) среды.


