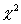Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая проверка гипотез в экологииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы. Студент должен знать: основные виды гипотез (нулевая, альтернативная), способы нахождения ошибок при проверке гипотез, критерий Фишера – Снедекора, критерий c2. Студент должен уметь: произвести статистическую проверку гипотез результатов проведенных экспериментов, а также проверять и применять различные законы распределения (Гаусса, Пуассона) для полученных в эксперименте величин с учетом погрешностей. Практическое значение выполняемых исследований При исследовании ряда задач, которые возникают в практике экологов, необходимо умелое использование методов статистической проверки гипотез. При этом очень важно определить параметры воздействия того или иного процесса (отходы промышленности, распространение микроорганизмов в водоеме). Статистическая проверка гипотез позволяет осуществлять анализ процессов (экопатогенных, биопатогенных). Данные практических экспериментов позволят приобрести обучаемому необходимые навыки в этом направлении. Литература 5. В.М. Еськов, О.Е. Филатова, В.А. Рачковская Статистическая обработка результатов измерений в практикуме по экологии и естествознанию.- Сургут: Изд. СурГУ, 1999.- 43 с. 6. М. Дж. Кендалл, А. Стьюарт. Теория распределений. М., 1998. – 213 с. 7. В. В. Гмурман. Теория вероятностей и математическая статистика. – М.: 8. Ю. В. Линник. Метод наименьших квадратов. – М. – 2001. – 196 с. Бюджет времени На изучение темы отводится 6 часов, из них 2 часа лекций, 2 часа лабораторные занятия и 2 часа на самоподготовку.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО I ЭТАПУ "Самоподготовка" Для подготовки к лабораторной работе Вам следует повторить материалы лекции. Ответьте на следующие вопросы: 1. Что такое нулевая гипотеза и конкурирующая? Для их применяют? 2. Что такое ошибки первого и второго рода? 4. Что такое генеральная совокупность? 3. Какие критерии применяют для проверки гипотез?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО II ЭТАПУ: “Выполнение лабораторной работы” Для выполнения этапа Вам предлагается выполнить следующие задания. При двух отдельных выборках исследовалась проблема заражения описторхозом рыб одной породы (язь) в двух разных частях реки Обь (под Сургутом и Нижневартовском). Были получены следующие данные: на 100 рыб в 9 пробах под Сургутом получили следующие проценты зараженных: 22, 24, 19, 17, 28, 31, 23, 24, 29. В 6 пробах под Нижневартовском: 17, 19, 21, 18, 25, 27. Необходимо: 1. С помощью F критерия Фишера проверить H0: D(x)=D(y) при H1: D(x)>D(y) (воспользоваться таблицей 1). 2. С помощью c2 проверить, что общепринятая другими учеными (по публикациям в научной литературе) D0=22 не отличается от D1(x) и D2(y) (по отдельности для каждой).
Блок информации Обработка экспериментального экологического материала не ограничивается данными о предполагаемом ряде распределения и его числовых характеристиках. Для полного представления о биообъекте необходимо получить определенные данные о виде предполагаемого распределения. В этом случае, например, высказывается гипотеза, что исследуемая генеральная совокупность распределения по закону A (например, нормальному или Пуассона). В других случаях выдвигают гипотезу о равенстве неизвестного параметра (дисперсии, например) такого закона (он получается из выборки) некоторому известному параметру (из литературы, например) или можно проверить равенство параметров (математического ожидания, дисперсии) двух выборок или двух уже найденных распределений и т.д. Например, возможна гипотеза: дисперсии 2-х нормальных распределений равны между собой или генеральная совокупность данной СВ распределена по закону Пуассона и т.д. Различают нулевую гипотезу H0 (выдвинутую) и конкурирующую (альтернативную) H1 , которая противоречит H0. Например, дисперсия нормального распределения D=2 а конкурирующая (H1) D¹2. Это записывается так: H0: D=2; (H1): D¹2. Бывают гипотезы простые, которые содержат только одно предположение, и сложные, например: H: M>1 утверждает, что содержится бесчисленное множество простых гипотез (математическое ожидание M может принимать любые значения из интервала >1). Выдвижение и проверка гипотез может приводить к ошибкам. Ошибка первого рода – это случай, когда будет опровергнута правильная гипотеза. Ошибки второго рода – будет принята неправильная гипотеза. Между ними существует различие. Если будет принято неправильное решение, например, “продолжить сброс промышленных стоков в водоем”, то оно может повлечь за собой гибель растений, животных и даже человека. Если же будет отвергнуто правильно решение “продолжить сброс промышленных стоков в водоем” (например, ПДК еще позволяет это делать), то ничего страшного для флоры и фауны не произойдет. В любом случае возникает задача проверки гипотез и делать это надо в каждом случае определенным (адекватно гипотезам) образом. Мы сейчас рассмотрим ряд наиболее типичных, характерных задач, которые возникают в практике экологов и их умелое использование в рамках системного подхода позволяет избежать трагических последствий. Для этого введем прежде всего, понятие статистического критерия (просто критерия K), который служит для проверки нулевой гипотезы. Пусть мы выдвигаем гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей. Такая задача может возникнуть, например, если вы производили замеры концентраций микроорганизмов в одном и том же водоеме, но в разных сериях опытов (например, на прошлой неделе и на этой или в прошлом году и в этом, но условия были приблизительно одинаковы по действию экофакторов). Следует отметить, что каждый критерий имеет свои законы распределения и очень часто эти критерии имеют специальные названия. Например, при проверке нулевой гипотезы специально подобранная величина обозначается через U или Z, если она нормально распределена, F или J2 – по закону Фишера-Снедекора, T – по закону Стьюдента, c2 – по закону “хи квадрат” и т.д. Рассмотрим конкретные примеры. Пример 1. Пусть по двум выборкам с объемами n1=12 (число взятых проб воды с исследуемыми организмами) и n2=15 (например, 12 проб брали неделю назад а 15 – сегодня), которые извлекались из нормальных генеральных совокупностей X и Y, были найдены две выборочные дисперсии Dx=11,41 и Dy=6,52. Требуется при уровне значимости 0,05 (аналог доверительной вероятности b в лаб. № 8) проверить нулевую гипотезу: H0: D(x)=D(y) о равенстве генеральных дисперсий (иными словами с биотой за неделю ничего существенного не произошло по оценке дисперсий) при конкурирующей гипотезе H1: D(x)>D(y). Для проверки гипотезы найдем F (критерий Фишера) Fнабл.=11,41/6,52=1,75. Поскольку D(x)>D(y), то критическая область – правосторонняя (D(x) справа от D(y)). По таблице 1 для степеней свободы K1=12-1=11 и K2=15-1=14 находим критическую точку Fкр.(8,05;11,14)=2,56. У нас получилось, что Fнабл.<Fкр., т.е. нет оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. В теории статистической проверки гипотез возможны различные задачи. Довольно часто возникает проблема, когда уже известна дисперсия генеральной совокупности (из литературных, научных данных) и надо сравнить полученную из выборки дисперсию D с генеральной D0. Для этого используется c2 критерий, где, c2 =(n-1) D/D0. Рассмотрим пример. По выборке n=13 найдена выборочная дисперсия D=14,6 (характеризует, например, процент заражения описторхисом рыбы определенного вида в Оби). Требуется при уровне значимости a=0,01 проверить нулевую гипотезу H0: D=D0=12 (т.е. в литературе известно, что D0=12), приняв в качестве конкурирующей гипотезы H1: D>12. Определим, c2=(n-1)D/D0=((13-1)x14,6)/12=14,6. По условию, конкурирующая гипотеза имеет вид D>12, поэтому критическая область правосторонняя. По таблице 1 для K=12 и a=0,01 находим критическую точку, c2кр. (0,01;12)=26,2. Поскольку, c2набл.<, c2кр., то нет оснований отвергнуть нулевую гипотезу, т.е. различие между выборочной D и гипотетической генеральной дисперсией – незначительное. Довольно часто возникают задачи сравнения двух средних нормальных генеральных совокупностей, дисперсии которых известны (независимые выборки). В этом случае выдвигают нулевую гипотезу H0:M(x)=M(y) при конкурирующей гипотезе Hi: M(x)¹M(y). В этом случае строят двустороннюю критическую область, при чем вероятность попадания критерия в эту область при справедливости нулевой гипотезы равна a/2, т.е. P(Z<Zлев.кр.)=a/2, P(Z<Zправ.кр.)=a/2. Для этих целей используют функцию Лапласа Ф(Z), где Z находят из уравнения Zнабл.=(x-y)/ Ö D(x)/n+D(y)/m, а критическую точку находят через Ф(Zкр.)=(1-a)/2 и таблицы функции Лапласа. Наконец, при сравнении двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки) используют T критерий Стьюдента с k=n+m-2 степенями свободы. Здесь
T=((x-y)/Ö(n-1)xDx+(m-1)xDy)xÖnm(n+m-2)/n+m Пример 2. В некоторых случаях может быть поставлен вопрос: полученная нами экспериментально какая - либо величина (например, ускорение свободного падения g или удельный заряд электрона е/m) совпадает с известными в теории величинами с учетом погрешностей? Или такой вопрос: распределение нашей СВ подчиняется закону Гаусса или Пуассона? Эти вопросы относятся к области статистической проверки гипотез и в рамках существующих критериев можно дать точный ответ на них. Для ответа на первый вопрос достаточно вычислить T - критерий по формуле
где хo - известная из теории величина (например, для ускорения свободного падения в данный местности известно, что хo=go=9.82 м/с2), Пример. При определении ускорения свободного падения g в 4-х опытах методом маятника было получено
и сравним с tkb=t3,0.9=2.35 (см. таблицу критерия стьюдента). Отсюда видно, что Т< tkb, поэтому выборочная средняя Отметим, что используя формулу
можно определить минимальный объем выборки n (число измерений), достаточное для сравнения выборочной (
можно определить n. Задача, правда несколько усложняется, если n<30, тогда tkb зависит от n и надо определить верность (12.2) перебором значений n или известными методами поиска с использованием ЭВМ. Таким образом, мы получаем эффективный способ отыскания грубых ошибок в методике эксперимента, что весьма важно в любой НИРС. Проверка гипотез о законе распределения также осуществляется с использованием критериев согласия и с ней вы можете познакомиться в специальной литературе.
Таблица 1 Таблица критических точек распределения
Таблица 2 Значение коэффициента нормированных отклонений (Стьюдента). Тkb для различных "k" и "b"
Лабораторная работа №13. Элементы дисперсионного анализа (ДА)
Цель работы. Студент должен знать: понятие дисперсионного анализа, понятие однофакторного и многофакторного ДА, понятия общей факторной и остаточной суммы. Студент должен уметь: по результатам экспериментов рассчитать факторную и остаточную дисперсии и по критерию F проверить справедливость гипотезы о различии групповых средних в целом.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.009 с.) |

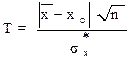 , (12.1)
, (12.1)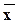 - вычисленная средняя арифметическая СВ,
- вычисленная средняя арифметическая СВ,  - статистическое среднее квадратическое отклонение (см. предыдущие л.р.). Если T<tkb, то говорят, что нулевая гипотеза о равенстве генеральной средней
- статистическое среднее квадратическое отклонение (см. предыдущие л.р.). Если T<tkb, то говорят, что нулевая гипотеза о равенстве генеральной средней 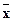 r и теоретической хo не отвергается, хотя само значение
r и теоретической хo не отвергается, хотя само значение  =9.7,
=9.7,  =0.2. Выдвигается нулевая гипотеза
=0.2. Выдвигается нулевая гипотеза  r=go, т.е. если поставить на этой установке множество опытов (получить генеральную совокупность), то
r=go, т.е. если поставить на этой установке множество опытов (получить генеральную совокупность), то 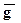 r будет ли равна 9.82 м/с2? Иными словами мы спрашиваем: чем закончатся наши исследования, если их проводить сколь угодно долго, - подтверждением, что go=9.82, или опровержением? Причем ответ мы дадим по малой выборке, так как n=4, k=n-1=3. Для этого определим
r будет ли равна 9.82 м/с2? Иными словами мы спрашиваем: чем закончатся наши исследования, если их проводить сколь угодно долго, - подтверждением, что go=9.82, или опровержением? Причем ответ мы дадим по малой выборке, так как n=4, k=n-1=3. Для этого определим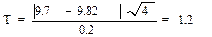
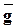 незначимо отличается от гипотетической генеральной средней go=9.82 м/с2 и опыт проводился корректно.
незначимо отличается от гипотетической генеральной средней go=9.82 м/с2 и опыт проводился корректно.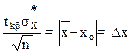
 , то из уравнения
, то из уравнения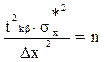 (12.2)
(12.2)