
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая значимость коэффициента корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Часто целью исследований является определение существования связей между с.в. X и Y. Поскольку коэффициент корреляции вычислен на основе выборочных данных, то не исключено, что его ненулевое значение является не отражением действительной связи между признаками, а просто получено в результате специфики данной выборки (тогда как в генеральной совокупности коэффициент корреляции равен нулю, т.е. линейной связи между признаками нет). В этом случае обычно проверяется статистическая гипотеза равенства нулю коэффициента корреляции, вычисленного по всей генеральной совокупности:
Статистика в этом случае описывается функцией
где
Лабораторная работа Задание 1. Нахождение выборочных характеристик Необходимо по заданной выборке, используя средства электронных таблиц, вычислить точечные оценки указанных параметров. Вычисления провести двумя способами и сравнить полученные результаты.
Задача 1.1. В рамках медицинского обследования были получены данные о росте у группы мужчин в количестве 101 человека. Результаты обследования приведены в следующей таблице: Таблица1. Выборка распределения значения роста у 101 мужчины
В первой колонке таблицы приведен номер обследуемого пациента, во второй – его рост. Требуется построить вариационный ряд, найти и сравнить выборочные характеристики ряда, полученные двумя способами: · вычислением по формуле, определяющей соответствующую характеристику · с использованием встроенной функции из библиотеки статистических функций EXCEL Для выполнения задания данные наблюдений необходимо перенести на рабочий лист электронной таблицы EXCEL, разместив их в двух первых колонках Таблица 2. Способы вычисления выборочных характеристик
(колонки Пояснения к таблице 2: При расчете по формулам объем выборки При расчете по формулам для вычисления среднего арифметического (выборочного среднего) используется формула ( При вычислении значения дисперсии по формулам необходимо использовать функции = СУММ(диапазон данных) и функцию =СЧЕТ(диапазон данных) ). Следует обратить внимание, что вычисление суммы при нахождении дисперсии проводится по отношению к квадрату разности Вычисление значения дисперсии с использованием библиотеки статистических функций производится с использованием функции =ДИСПР(диапазон данных ) [11] Стандартное (средне-квадратичное) отклонение Для вычисления некоторых оценок рекомендуется использовать ранжирование. Для этого необходимо скопировать исходные данные роста в некоторый столбец (запрещается изменение исходных данных без копирования, так как это ведет к потере исходной информации), с последующей сортировкой значений в новом столбце. После сортировки минимальные и максимальные значения находятся на противоположных концах построенного ряда. Минимальное и максимальное значение можно также рассчитать используя встроенные функции =МИН(диапазон данных) и = МАКС(диапазон данных)
Первый способ вычисления медианы в нахождении в отсортированной последовательности варианты, выше и ниже которой, в столбце значений находится одинаковое количество вариант. Для вычисления медианы вторым способом необходимо использовать функцию =МЕДИАНА(диапазон данных) Квартили – значения, отсекающие по 1/4 части вариационного ряда. Необходимо найти квартили для значений 0,25 и 0,75. Первый способ вычисления варианты для значения 0,25 заключается в нахождении в отсортированной последовательности варианты, выше которой в столбце значений находится четвертая часть значений ряда. Соответственно для вычисления 3-ей квартили необходимо найти значение варианты, выше которой находится ¾ значений вариационного ряда. Для вычисления значения квартили с использованием встроенной функции необходимо вызвать функцию =КВАРТИЛЬ(диапазон данных; номер квартиля) Ниже приведена таблица соответствия номеров квартиля и значений функции
Стандартную ошибку среднего арифметического и коэффициент вариации необходимо посчитать только с использованием формул. При вычислении значения коэффициента асимметрии по формулам необходимо использовать функции = СУММ(диапазон данных) и - функцию =СЧЕТ(диапазон данных) ). Следует обратить внимание, что вычисление суммы при нахождении дисперсии проводится по отношению к кубу разности При вычислении значения коэффициента эксцесса по формулам необходимо использовать функции = СУММ(диапазон данных) и- функцию =СЧЕТ(диапазон данных) ). Следует обратить внимание, что вычисление суммы при нахождении дисперсии проводится по отношению к четвертой степени разности
Алгоритм выполнения задания 1 по шагам [13]: 1. Запустить программу EXCEL. Набрать с клавиатуры данные по значениям роста для выборки из 101 мужчин, или при наличии электронного варианта таблицы, выделить и скопировать исходные данные через буфер обмена в первый лист программы EXCEL, расположив их в двух первых столбцах (A и B) рабочего листа. 2. Скопировать (или набрать с клавиатуры) наименования вычисляемых параметров, расположив их в столбцах G и H, предварительно расширив столбец H. (столбцы C,D,E,F необходимы для проведения промежуточных вычислений) 3. Вычислить значение объема выборки, используя функцию =СЧЕТ(диапазон данных) (в качестве диапазона данных выбирается столбец В (значения роста)). С этой целью, установить курсор в ячейку J2, нажав на кнопку
4. В ячейке I3 вычислить значение среднего арифметического по формуле 5. Вычислить значение среднего арифметического по формуле СРЗНАЧ(диапазон данных ). Сравнить результаты двух вычислений 6. Для расчета дисперсии в ячейке C1 вычислить значение формулы 7. Используя значения, полученные в шаге 6, в ячейке I4 вычислить значение дисперсии по формуле
8. Параллельно провести вычисление значения функции ДИСПР(диапазон данных). 9. В ячейке I5 вычислить значение стандартного отклонения как квадратный корень из дисперсии. Параллельно в ячейке J5 провести вычисления по формулам из статистической библиотеки. 10. Скопировать данные роста (столбец В) в ячейки столбца F и отсортировать скопированные данные (только в пределах столбца F) по неубыванию. Заполнить минимальное, максимальное значения ряда, медиану, квартили, указывая адреса ячеек, где расположены эти данные. Параллельно сосчитать эти данные по формулам из статистической библиотеки. 11. Подсчитать размах выборки, используя найденные значения максимума и минимума. 12. Рассчитать стандартную ошибку среднего арифметического и коэффициент вариации, используя найденные значения среднего арифметического и стандартное отклонение. 13. Рассчитать в ячейке D1 значение формулы 14. Рассчитать в ячейке E1 значение формулы
Задача 1.2. Дана таблица распределения числа различных типов правонарушений по районам некоторого региона. В каждом районе указано число жителей, проживающих в этом районе.
Требуется построить вариационный ряд (по показателям число правонарушений на одного жителя), найти выборочные характеристики данной выборки: · вычислением по формуле, определяющей соответствующую характеристику · с использованием встроенной функции из библиотеки статистических функций EXCEL
Задача 1.3. На предприятии работают 100 человек. В таблице приводится зарплата каждого из сотрудников данного предприятия:
Требуется построить вариационный ряд, найти выборочные характеристики данной выборки: · вычислением по формуле, определяющей соответствующую характеристику · с использованием встроенной функции из библиотеки статистических функций EXCEL
Задача 1.4. Изготавливается тираж книги, один из размеров которой должен быть 20 см. По опытному тиражу произведена оценка отклонений размера для 100 пробных экземпляров. Результаты измерений сведены в таблицу, где
Требуется построить вариационный ряд, найти выборочные характеристики данной выборки: · вычислением по формуле, определяющей соответствующую характеристику · с использованием встроенной функции из библиотеки статистических функций EXCEL Задача 1.5. Ниже приведены данные выборочного обследования семей по средне-душевому доходу (в у.е.)
Требуется построить вариационный ряд, найти выборочные характеристики данной выборки: · вычислением по формуле, определяющей соответствующую характеристику · с использованием встроенной функции из библиотеки статистических функций EXCEL Задача 1.6. В рамках обследования были получены данные о росте у группы женщин в количестве 101 человека. Результаты обследования приведены в следующей таблице: Таблица. Выборка распределения значения роста у 101 женщины
Требуется построить вариационный ряд, найти выборочные характеристики данной выборки: · вычислением по формуле, определяющей соответствующую характеристику · с использованием встроенной функции из библиотеки статистических функций EXCEL Задание 2 Построение гистограммы выборки При анализе статистических данных в большинстве случаев исследователю не доступна информация о законе распределения исходной случайной величины. Одним из способов оценивания функции распределения случайной величины является построение эмпирической функции распределения на базе имеющегося материала. Для построения эмпирической функции распределения необходимо представление выборки в сгруппированном виде с подсчетом разброса значений исходной с.в. по построенным по некоторому правилу интервалам с дальнейшим анализом полученных данных. Интервалы группирования зависят от природы задачи. Обычно внутренние интервалы выбираются одинаковой длины. Часто для определения числа интервалов используют формулы Старджеса Задача 2.1
Для данных, приведенных в задаче 1 предыдущего задания, построить гистограмму выборки, совместив его с графиком ожидаемой функции плотности. В качестве ожидаемой функции рассмотреть функцию плотности нормального распределения. Для построения гистограммы необходимо выполнить следующую последовательность действий: · Построить исходную выборку · Выбрать длину интервала и разбить область значений выборки на заданное число · Для каждого интервала подсчитать число вариант, попавших в данный интервал · Построить формулу для предполагаемой теоретической плотности · Построить график ступенчатой кривой, у которой высота ступеньки над · Наложить на гистограмму график кривой нормального распределения, определяемого параметрами (среднее значение, стандартное отклонение) заданной выборки.
При подсчете числа попаданий в заданные интервалы удобно использовать функцию ЧАСТОТА, предназначенную для подсчета количеств попаданий значений с.в. в заданные интервалы разбиений числовой оси прямой. Она относится к классу так называемых функций массива. Для ее вызова необходимо: 1. Положить длину интервала 2. Для заданной выборки найти минимальное и максимальные значения роста и записать данные в таблицу. Положить границу первого интервала равной =МИН(диапазон данных)-h/2 3. В некотором столбце, например в ячейках с адресами B2:B15 начав с границы первого интервала с использованием формул арифметической прогрессии перечислить границы интервалов группировок длины h. 4. Выделить диапазон ячеек, в которые необходимо записать количество попаданий значений роста в соответствующие и
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.218.107 (0.014 с.) |

 при альтернативе
при альтернативе 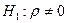 . Критерием для проверки нулевой гипотезы о равенстве нулю генерального коэффициента корреляции совокупности (или соответственно о независимости случайных величин X и Y) является отношение выборочного коэффициента корреляции к своей ошибке
. Критерием для проверки нулевой гипотезы о равенстве нулю генерального коэффициента корреляции совокупности (или соответственно о независимости случайных величин X и Y) является отношение выборочного коэффициента корреляции к своей ошибке .
. ,
,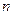 - объем выборки. Число степеней свободы для проверки критерия равно
- объем выборки. Число степеней свободы для проверки критерия равно  . Далее гипотезу проверяют по таблицам распределения Стьюдента в соответствие с выбранным уровнем значимости. Если полученное значение статистики окажется больше или равным соответствующего табличного значения, нулевую гипотезу отвергают. Другой вариант проверки заключается в построении 95% доверительного интервала для вычисленного значения коэффициента корреляции и проверки попадания нулевого значения в этот интервал. Если ноль не содержится в построенном доверительном интервале, то с вероятностью 0,95 исследуемые величины имеют зависимость в генеральной совокупности (коэффициент корреляции является статистически значимым), в противном случае - с высокой вероятностью в генеральной совокупности может оказаться нулевая корреляция, т.е. отсутствие связи (коэффициент корреляции является статистически незначим). Необходимо подчеркнуть, что величина коэффициента корреляции еще не гарантирует его значимости: даже большой коэффициент может оказаться статистически незначимым (например, при малом объеме выборки), а небольшой коэффициент (если выборка велика) - значимым.
. Далее гипотезу проверяют по таблицам распределения Стьюдента в соответствие с выбранным уровнем значимости. Если полученное значение статистики окажется больше или равным соответствующего табличного значения, нулевую гипотезу отвергают. Другой вариант проверки заключается в построении 95% доверительного интервала для вычисленного значения коэффициента корреляции и проверки попадания нулевого значения в этот интервал. Если ноль не содержится в построенном доверительном интервале, то с вероятностью 0,95 исследуемые величины имеют зависимость в генеральной совокупности (коэффициент корреляции является статистически значимым), в противном случае - с высокой вероятностью в генеральной совокупности может оказаться нулевая корреляция, т.е. отсутствие связи (коэффициент корреляции является статистически незначим). Необходимо подчеркнуть, что величина коэффициента корреляции еще не гарантирует его значимости: даже большой коэффициент может оказаться статистически незначимым (например, при малом объеме выборки), а небольшой коэффициент (если выборка велика) - значимым.

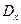
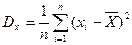
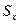

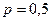 )
)
 )
)




 и
и 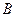 ) таким образом, что в первой колонке будет записан номер пациента, а во второй – его рост. Далее, используя приведенные формулы и встроенные статистические функции в библиотеке функций EXCEL, вычислить и сравнить между собой значения выборочных характеристик. В таблице 2 приведен список формул для вычисляемых значений с указанием библиотечных функций EXCEL
) таким образом, что в первой колонке будет записан номер пациента, а во второй – его рост. Далее, используя приведенные формулы и встроенные статистические функции в библиотеке функций EXCEL, вычислить и сравнить между собой значения выборочных характеристик. В таблице 2 приведен список формул для вычисляемых значений с указанием библиотечных функций EXCEL - варианта выборки(значение роста
- варианта выборки(значение роста  -го человека),
-го человека), 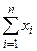 необходимо использовать функцию = СУММ(диапазон данных), а значение
необходимо использовать функцию = СУММ(диапазон данных), а значение 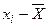 , который необходимо вычислить для значения каждой варианты
, который необходимо вычислить для значения каждой варианты 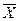 одно и то же для всех значений
одно и то же для всех значений 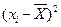 производится для одного индивида, а затем тиражируется на всех пациентов с использованием технологий, имеющихся в электронных таблицах.
производится для одного индивида, а затем тиражируется на всех пациентов с использованием технологий, имеющихся в электронных таблицах. перейти в режим набора формул и выбрать строку «СЧЕТ» из выпадающего списка с наименованием формул. Далее необходимо указать диапазон исходных данных, который для данного параметра определяется данными столбца В.
перейти в режим набора формул и выбрать строку «СЧЕТ» из выпадающего списка с наименованием формул. Далее необходимо указать диапазон исходных данных, который для данного параметра определяется данными столбца В.
 с использованием функции = СУММ(диапазон данных) и имеющегося объема выборки. Формула расчета параметра выглядит следующим образом: =СУММ(B1:B101)/ J2
с использованием функции = СУММ(диапазон данных) и имеющегося объема выборки. Формула расчета параметра выглядит следующим образом: =СУММ(B1:B101)/ J2 с последующим тиражированием построенной формулы на весь вариационный ряд (ячейки С1:С101). При вычислении формулы необходимо обратить внимание на адрес среднего арифметического. Этот адрес должен быть не относительным, а абсолютным (не должен меняться при копировании формул), и должен быть набран с использованием знака $. Окончательная формула для ячейки C1 должна выглядеть следующим образом: =(B1-J$2)*(B1-J$2).
с последующим тиражированием построенной формулы на весь вариационный ряд (ячейки С1:С101). При вычислении формулы необходимо обратить внимание на адрес среднего арифметического. Этот адрес должен быть не относительным, а абсолютным (не должен меняться при копировании формул), и должен быть набран с использованием знака $. Окончательная формула для ячейки C1 должна выглядеть следующим образом: =(B1-J$2)*(B1-J$2).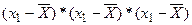 , протиражировать построенную формулу с использованием данных всего столбца В, и посчитать по формуле коэффициент асимметрии. Параллельно в ячейке J14 провести вычисления по формулам из статистической библиотеки.
, протиражировать построенную формулу с использованием данных всего столбца В, и посчитать по формуле коэффициент асимметрии. Параллельно в ячейке J14 провести вычисления по формулам из статистической библиотеки. , протиражировать построенную формулу на данные всего столбца E и посчитать коэффициент эксцесса. Параллельно в ячейке J15 провести вычисления по формулам из статистической библиотеки.
, протиражировать построенную формулу на данные всего столбца E и посчитать коэффициент эксцесса. Параллельно в ячейке J15 провести вычисления по формулам из статистической библиотеки.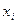 отклонение в сотых долях мм
отклонение в сотых долях мм 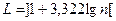 , где
, где  означает наименьшее целое число большее или равное
означает наименьшее целое число большее или равное  . На практике значение
. На практике значение  можно полагать равным
можно полагать равным  . На первом шаге формируется вариационный ряд
. На первом шаге формируется вариационный ряд  (данные упорядочиваются по неубыванию:
(данные упорядочиваются по неубыванию: 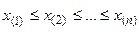 ), вычисляется длина интервалов
), вычисляется длина интервалов  . Иногда, чтобы
. Иногда, чтобы 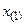 и
и 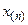 попали внутрь интервалов, границы интервалов подсчитываются по формулам:
попали внутрь интервалов, границы интервалов подсчитываются по формулам:  и
и 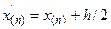 . При этом число интервалов увеличивается на 1, а границы интервалов образуют следующую последовательность
. При этом число интервалов увеличивается на 1, а границы интервалов образуют следующую последовательность  . Далее определяется количество элементов попадания элементов выборки в каждый интервал и по полученным данным строится гистограмма. При графическом изображении интервальных вариационных рядов распределения, частоты выражаются в виде прямоугольников соответствующей длины. По оси абсцисс откладываются значения признака. На этих отрезках строятся прямоугольники, которые сомкнуты друг с другом, с равными основаниями и площади которых пропорциональны вычисленным частотам. Полученный ступенчатый многоугольник, состоящий из определенного числа следующих друг за другом прямоугольников различной высоты, называется гистограммой. Часто на гистограмму накладывают график функции плотности некоторого известного распределения. Поскольку гистограмма строится по имеющейся выборке, она отражает функцию распределения искомой случайной величины с некоторым приближением. Визуально сравнить гистограмму выборки с теоретической кривой плотности некоторого известного распределения.
. Далее определяется количество элементов попадания элементов выборки в каждый интервал и по полученным данным строится гистограмма. При графическом изображении интервальных вариационных рядов распределения, частоты выражаются в виде прямоугольников соответствующей длины. По оси абсцисс откладываются значения признака. На этих отрезках строятся прямоугольники, которые сомкнуты друг с другом, с равными основаниями и площади которых пропорциональны вычисленным частотам. Полученный ступенчатый многоугольник, состоящий из определенного числа следующих друг за другом прямоугольников различной высоты, называется гистограммой. Часто на гистограмму накладывают график функции плотности некоторого известного распределения. Поскольку гистограмма строится по имеющейся выборке, она отражает функцию распределения искомой случайной величины с некоторым приближением. Визуально сравнить гистограмму выборки с теоретической кривой плотности некоторого известного распределения. -м интервалом пропорциональна числу вариант, попавших в этот интервал.
-м интервалом пропорциональна числу вариант, попавших в этот интервал. =5.
=5.


