
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функции распределенияСодержание книги
Поиск на нашем сайте
1. 2. 3. 4. Если возможные значения случайной величины принадлежат интервалу Квантили: При решении вероятностно-статистических задач применяется понятие «квантиль порядка р» (обозначается) Пример 3. Найдем квантиль Решение. При 0 < p < 1 квантиль Большую роль в статистике играет квантиль Медиана указывает «центр» распределения. Точки Другой характеристикой случайной величины является мода – значение (или значения) случайной величины, соответствующее локальному максимуму плотности вероятности для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины. У случайной величины может быть много мод. Так, для равномерного распределения каждая точка х такая, что Каждая из трех характеристик – математическое ожидание, медиана, мода – по своему описывает «центр» распределения вероятностей. Однако для важного класса распределений – симметричных унимодальных – все три характеристики совпадают. Распределение с плотностью Отметим еще одно свойство симметричных распределений, постоянно используемое в вероятностно-статистических методах принятия решений и других прикладных исследованиях. Для непрерывной функции распределения Если Коэффициент вариации – это отношение среднего квадратичного отклонения к математическому ожиданию:
Коэффициент вариации применяется при M(X)> 0 и измеряет разброс в относительных единицах, в то время как среднее квадратичное отклонение – в абсолютных. Для каждой случайной величины
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.44.115 (0.009 с.) |

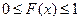
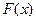 - неубывающая функция:
- неубывающая функция: 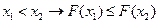
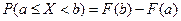
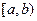 , то при
, то при 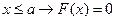 и
и 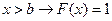
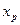 , где
, где 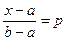 , т.е.
, т.е. 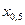 порядка
порядка 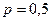 . Он называется медианой (случайной величины Х или ее функции распределения F(x)) и обозначается Me(X). Медиана определяет значение на числовой оси, для которой вероятность для случайной величины попасть левее
. Он называется медианой (случайной величины Х или ее функции распределения F(x)) и обозначается Me(X). Медиана определяет значение на числовой оси, для которой вероятность для случайной величины попасть левее 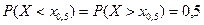 .
.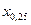 и
и 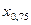 называются квартилями и вместе с медианой делят область значения случайной величины на 4 части, вероятности попадания в которые равны
называются квартилями и вместе с медианой делят область значения случайной величины на 4 части, вероятности попадания в которые равны 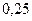 .
.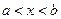 , является модой. Однако этот пример скорее является исключением. Большинство случайных величин, используемых в вероятностно-статистических методах принятия решений и других прикладных исследованиях, имеют единственную моду. Случайные величины, плотности, распределения, имеющие одну моду, называются унимодальными.
, является модой. Однако этот пример скорее является исключением. Большинство случайных величин, используемых в вероятностно-статистических методах принятия решений и других прикладных исследованиях, имеют единственную моду. Случайные величины, плотности, распределения, имеющие одну моду, называются унимодальными.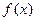 называется симметрическим, если найдется такое число
называется симметрическим, если найдется такое число 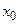 , что
, что 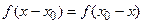 для любого
для любого  . Это соотношение означает, что график функции
. Это соотношение означает, что график функции 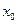 . Для функции симметричного распределения имеем
. Для функции симметричного распределения имеем 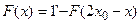 . При
. При 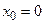 соответственно имеем
соответственно имеем 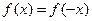 и
и 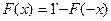 . Приведенные соотношения показывают, что в случае симметричных распределений нет необходимости вычислять
. Приведенные соотношения показывают, что в случае симметричных распределений нет необходимости вычислять 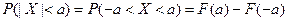 , где F – функция распределения случайной величины Х. Если функция распределения F симметрична относительно 0, то
, где F – функция распределения случайной величины Х. Если функция распределения F симметрична относительно 0, то 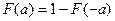 . Тогда
. Тогда 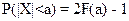 . Часто используют другую формулировку рассматриваемого утверждения: если
. Часто используют другую формулировку рассматриваемого утверждения: если 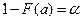 , то
, то 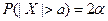 .
.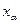 и
и 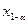 - квантили порядка
- квантили порядка  и
и 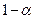 соответственно для функции распределения, симметричной относительно 0, то
соответственно для функции распределения, симметричной относительно 0, то 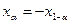 .
.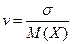 .
. можно построить центрированную с.в.
можно построить центрированную с.в. 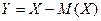 , математическое ожидание которой равно 0, а
, математическое ожидание которой равно 0, а 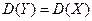 . С.в.
. С.в. 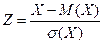 называется нормированной. Нетрудно проверить, что
называется нормированной. Нетрудно проверить, что  и
и 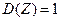 .
.


