Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование зависимости между двумя характеристикамиСодержание книги
Поиск на нашем сайте
При анализе поведения различных объектов часто возникают задачи изучения глубины и формы различных связей между параметрами системы. Знание таких связей позволяет прогнозировать изменения одних параметров по результатам изменения других, выявлять факторы, изменения которых может позволить получить необходимые значения исследуемых параметров. Поэтому одной из основных задач анализа данных является определение глубины связей между различными параметрами изучаемого объекта (ростом и весом человека, данных по числу правонарушений в определенных регионах в различные периоды времени и уровнем жизни населения, зависимость между степенью подготовки студента и оценкой на экзамене и т.п.). Раздел статистики, занимающийся подобными вопросами, называется корреляционным анализом. Основными задачами корреляционного анализа являются: 1. выявление характера и степени зависимости между исследуемыми параметрами 2. построение уравнения наилучшего прогноза одной характеристики по значениям другой Различают два типа связей: функциональную и стохастическую. Связь называется функциональной, если значению одной переменной обязательно соответствует одно значение другой переменной. Примерами функциональной связи являются соотношения вида
Совокупность точек плоскости на диаграмме создает общую картину корреляции и обычно позволяет строить некоторую усредненную кривую взаимозависимости значений параметров, составляющих наблюдаемые вариационные ряды. Соответствующая кривая называется линией регрессии, которая является характеристикой связи и часто используется для некоторого прогноза поведения в среднем соответствующих с.в.
Обозначим через X, Y наблюдаемые в эксперименте случайные величины. Допустим, предполагается осуществлять прогноз, используя некоторую функциональную зависимость
где
Коэффициент корреляции выражает степень «линейной связи». Такая интерпретация обусловлена следующими свойствами этого коэффициента: 1. значения коэффициента лежат между –1 и 1 и не зависят от масштаба измерений; 2. коэффициент корреляции симметричен, т.е. не изменяется, если X и Y поменять местами. 3. если 4. если случайные величины Y и X независимы, то Неизвестные параметры
- выборочный коэффициент корреляции между Y и X. Оценку уравнения регрессии Y на X можно записать в виде:
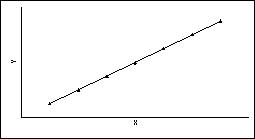
Приведенное уравнение называют выборочным уравнением регрессии Y на X, а ее график – выборочной линией регрессии Y на X. Аналогично при построении регрессии X на Y получаем уравнение Таким образом, обе линии регрессии проходят через точку с координатами В заключении еще раз отметим основные характеристики такой меры связи: 1. Какова бы ни была конфигурация облака точек на диаграмме рассеяния – лежат ли они в точности на одной прямой или разбросаны хаотически, всегда можно построить уравнение регрессии. Однако в первом случае (точки лежат на одной прямой) оно будет весьма достоверным (функциональным), а во втором (точки разбросаны хаотически) – нет. 2. Поскольку линия регрессии отслеживает связь между средними показателями, то одна и та же линия может соответствовать различным диаграммам рассеивания 3. Линия регрессии сама по себе не дает ответа на вопрос о тесноте (силе) связи пары переменных. На этот вопрос отвечает коэффициент парной корреляции. Он показывает, насколько тесно две переменные связаны между собой. Визуально о силе связи можно судить по тому, насколько близко расположены точки-объекты около линии регрессии. Чем ближе точки к линии регрессии, тем сильнее связь. 4. Если r = 1, то между двумя переменными существует функциональная положительная линейная связь, т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с положительным наклоном:
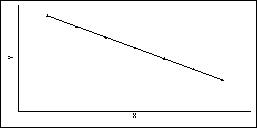
Если r=–1, то между двумя переменными существует функциональная отрицательная линейная зависимость, т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с отрицательным наклоном.
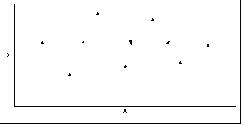
Если r = 0, то рассматриваемые переменные линейно независимы, т.е. на диаграмме рассеяния облако точек "вытянуто по горизонтали".
Положительные значения коэффициента корреляции r свидетельствуют о положительной связи между признаками, отрицательные – об отрицательной связи.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.76 (0.007 с.) |

 или
или  . В реальной природе функциональная связь встречается крайне редко и в большей степени является формальной абстракцией, упрощающей изучаемые модели. Стохастическая связь представляет такую зависимость между величинами, при которой одинаковым значениям одной переменной соответствуют разные значения другой переменной (например, значение роста от веса; значение курса одной валюты относительно другой; число преступлений за определенный период времени в определенном регионе). Такое положение вещей, прежде всего, связано с тем, что зависимая переменная подвержена влиянию ряда неучтенных или неконтролируемых случайных факторов. Поэтому значения зависимой переменной не могут быть предсказаны точно, а указаны с определенной вероятностью. Корреляционная связь представляет частный случай стохастической связи, при которой разным значениям одной переменной соответствуют различные средние значения другой. Наглядно эта связь может быть отражена графически. На координатной плоскости по оси абсцисс откладывают значения одного вариационного ряда, а по оси ординат – другого. Такие диаграммы называются диаграммами рассеивания. Ниже приведена такая диаграмма зависимости между ростом и весом для некоторого множества людей
. В реальной природе функциональная связь встречается крайне редко и в большей степени является формальной абстракцией, упрощающей изучаемые модели. Стохастическая связь представляет такую зависимость между величинами, при которой одинаковым значениям одной переменной соответствуют разные значения другой переменной (например, значение роста от веса; значение курса одной валюты относительно другой; число преступлений за определенный период времени в определенном регионе). Такое положение вещей, прежде всего, связано с тем, что зависимая переменная подвержена влиянию ряда неучтенных или неконтролируемых случайных факторов. Поэтому значения зависимой переменной не могут быть предсказаны точно, а указаны с определенной вероятностью. Корреляционная связь представляет частный случай стохастической связи, при которой разным значениям одной переменной соответствуют различные средние значения другой. Наглядно эта связь может быть отражена графически. На координатной плоскости по оси абсцисс откладывают значения одного вариационного ряда, а по оси ординат – другого. Такие диаграммы называются диаграммами рассеивания. Ниже приведена такая диаграмма зависимости между ростом и весом для некоторого множества людей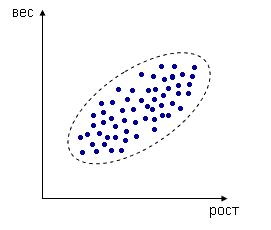

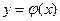 . Естественно возникает задача выбора функции, для которой минимизируется ошибка прогноза в заданных точках. Существует метод построения функции, которая минимизирует среднеквадратичную ошибку в отклонениях данных от значений, задаваемых функцией
. Естественно возникает задача выбора функции, для которой минимизируется ошибка прогноза в заданных точках. Существует метод построения функции, которая минимизирует среднеквадратичную ошибку в отклонениях данных от значений, задаваемых функцией 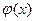 (минимизируется сумма квадратов отклонений значений ординат данных от ближайших точек функции). Построенная таким образом функция называется функцией регрессии Y на X, а соответствующий график этой функции – линией регрессии. На практике рассматривают построение функции
(минимизируется сумма квадратов отклонений значений ординат данных от ближайших точек функции). Построенная таким образом функция называется функцией регрессии Y на X, а соответствующий график этой функции – линией регрессии. На практике рассматривают построение функции 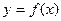 регрессии в классе линейных функций. Уравнение линейной функции, минимизирующей среднеквадратичную ошибку, имеет вид:
регрессии в классе линейных функций. Уравнение линейной функции, минимизирующей среднеквадратичную ошибку, имеет вид: ,
, - среднее значение и средне-квадратичное отклонение с.в. X
- среднее значение и средне-квадратичное отклонение с.в. X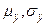 - среднее значение и средне-квадратичное отклонение с.в. Y,
- среднее значение и средне-квадратичное отклонение с.в. Y,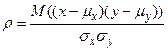 - коэффициент корреляции между Y и X.
- коэффициент корреляции между Y и X.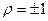 , то существует точная линейная связь, причем при
, то существует точная линейная связь, причем при 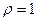 , эта связь положительная (обе характеристики растут одновременно), а при
, эта связь положительная (обе характеристики растут одновременно), а при 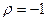 - отрицательная
- отрицательная
 и
и  линейной регрессии оцениваются своими выборочными аналогами
линейной регрессии оцениваются своими выборочными аналогами 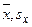 ,
, 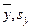 и
и 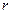 , где
, где 

 , которое при построении графика (чтобы выразить зависимость Y от X) обычно приводится к виду
, которое при построении графика (чтобы выразить зависимость Y от X) обычно приводится к виду 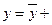
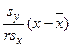 .
.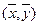 , и отличаются лишь коэффициентом наклона
, и отличаются лишь коэффициентом наклона