
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайное событие и вероятностьСодержание книги
Поиск на нашем сайте
Теория вероятностей изучает закономерности, возникающие в случайных экспериментах. Случайным называют эксперимент, результат которого нельзя предсказать заранее и в котором наблюдается устойчивость в появлении относительного числа событий. Испытанием называется реализация определенного комплекса условий, который может воспроизводиться неограниченное число раз. При этом комплекс условий включает в себя случайные факторы, реализация которых в каждом испытании приводит к неоднозначности исхода испытания. Например, при многократном подбрасывании монеты результат подбрасывания зависит от многих факторов: от силы броска, от скорости вращения, от того, какой стороной лежит монета в момент броска, и т.д. Результатом испытания является элементарное событие. Множество всех элементарных событий образует пространство Наблюдаемые события разбиваются на следующие три класса: · Достоверные – события, которые обязательно происходят, если будет осуществлена определенная совокупность условий; Примером достоверного события является событие · Невозможные – события, которые никогда не происходят, если будет осуществлена определенная совокупность условий; В частности мы никогда не наблюдаем событие, что при подбрасывании кубик становится на ребро. Для обозначения невозможного события используется символ Æ. · Случайные –события, которые при осуществлении определенной совокупности условий могут как произойти, так и не произойти. Примерами случайных событий являются события
Сложное событие наступает тогда и только тогда, когда в результате испытаний произошло некоторое элементарное событие, входящему в это сложное событие. Например, выпадение грани с номером “4” влечет наступление событий Дополнением
Произведением (пересечением) событий
События Полной группой событий называется конечный набор или счетная последовательность попарно несовместных событий
Квантор Множество событий вместе с набором перечисленных выше операций образуют алгебру событий. Используя операции этой алгебры можно строить достаточно сложные по своей структуре события. При этом одно и то же событие может быть выражено различными формулами. Формулы, которые выражают одинаковые события, называют эквивалентными и соединяют знаком равенства. Например, Определение вероятности Возможность наступления различных событий может различаться. Будем считать более вероятными те события, которые происходят чаще, менее вероятными - те, которые происходят реже; маловероятными - те, которые вообще не происходят. Например, событие "температура выше 30-ти градусов тепла в июле" более вероятно, чем "выпадение снега в Казани тот же день", а событие "появление шаровой молнии" крайне мало вероятно. Поэтому, понятие вероятности события с самого начала тесно увязывается с понятием его частоты. Каждому событию приписывается некоторое число, называемое его вероятностью и характеризующее степень возможности реализации этого события. При этом достоверному событию приписывается вероятность 1, а невозможному событию вероятность 0. Все остальные события имеют вероятности, лежащие между нулем и единицей. Пусть множество W состоит из конечного
Более строго, модель можно описать следующим образом: Пусть Таким образом, вероятность показывает степень возможности осуществления данного события. Приведенное выше определение вероятности описывает достаточно частный случай и применимо только для конечного пространства элементарных событий. В общем случае теория вероятностей опирается на аксиоматическое определение вероятности, предложенное академиком А.Н. Колмогоровым (в данном учебном пособии не рассматривается). Этот подход позволил рассматривать теорию вероятностей и математическую статистику с математических позиций, проводить рассуждения на математическом уровне строгости. В частности, было введено четкое различие между частотой и вероятностью, случайная величина стала рассматриваться как функция от элементарного исхода, и т.д. Пример 1.1. Бросили симметричную игральную кость. Какова вероятность того, что выпала грань, помеченная числом 3? Решение: Всего существует 6 вариантов выпадения кости (n = 6). Все эти варианты равновозможны, т.к. кость симметрична. Нас интересует единственный исход, следовательно, m = 1; значит Пример 1.2. Какова вероятность того, что при бросании игральной кости выпадет нечетное число очков? Решение: Благоприятных возможностей здесь три: 1; 3; 5. Поэтому m = 3, всего исходов 6 (n = 6), следовательно Пример 1.3. Бросают 2 игральные кости и сравнивают сумму выпавших очков. Что вероятней – получить в сумме 7 или 8? Решение: В этой задаче нас интересуют события Событию B будут благоприятствовать исходы: (2;6); (3;5); (4;4); (5;3); (6;2), т.е. всего 5. По формуле, имеем: Однако вычисление вероятности события Если мы интересуемся событием Интуиция подсказывает, что частота наступления случайного события зависит не только от степени случайности самого события. Если мы наблюдали за событием Пример 1.4 Вероятность выпадения решки при подбрасываниях симметричной монеты, может быть вычислена как предельное значение частоты выпадения соответствующей стороны монеты при достаточно большом числе испытаний (каждое испытание заключается в однократном подбрасывании монеты с фиксацией выпадения решки). В таблице приведены результаты трех исследований, состоящих в многократном бросании симметричной монеты
Как видно, частота появления герба в сериях экспериментов мало отличается от 0,5 и с увеличением числа испытаний погрешность уменьшается. Таким образом, вероятность можно рассматривать в качестве предела, к которому стремится частота наблюдения за событием при непрерывном увеличении числа наблюдений. Теория вероятностей доказывает существование такого предела и сходимость частоты к вероятности при стремлении числа наблюдений к бесконечности. Это положение носит название закона больших чисел.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.01 с.) |

 элементарных событий. Под сложным событием (далее просто событие) понимается произвольное подмножество множества элементарных событий. Например, при подбрасывании симметричного кубика пространство
элементарных событий. Под сложным событием (далее просто событие) понимается произвольное подмножество множества элементарных событий. Например, при подбрасывании симметричного кубика пространство  , каждое из которых нумерует определенную грань кубика. В качестве событий можно рассматривать событие
, каждое из которых нумерует определенную грань кубика. В качестве событий можно рассматривать событие  выпадения нечетной грани
выпадения нечетной грани  или выпадение числа очков более 3 (
или выпадение числа очков более 3 ( ), или выпадение четной грани
), или выпадение четной грани  , выпадение какой либо грани (
, выпадение какой либо грани ( ).
). , которое состоит из всех элементарных событий.
, которое состоит из всех элементарных событий. и
и  (В дальнейшем, для обозначения событий будем использовать заглавные символы латинского алфавита).
(В дальнейшем, для обозначения событий будем использовать заглавные символы латинского алфавита). События удобно изображать графически в виде рисунка, который называется диаграммой Венна. Обычно пространство элементарных исходов W изображают в виде прямоугольника, а множество элементарных исходов, благоприятствующих событию A в виде эллипса. Такие рисунки называются диаграммами Венна. Сами исходы на диаграммах Венна не изображаются, а информация о соотношении между их множествами содержится в расположении границ соответствующих областей.
События удобно изображать графически в виде рисунка, который называется диаграммой Венна. Обычно пространство элементарных исходов W изображают в виде прямоугольника, а множество элементарных исходов, благоприятствующих событию A в виде эллипса. Такие рисунки называются диаграммами Венна. Сами исходы на диаграммах Венна не изображаются, а информация о соотношении между их множествами содержится в расположении границ соответствующих областей.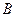 ,
,  события
события 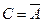 ).
). Суммой(объединением) двух событий
Суммой(объединением) двух событий  . Событие
. Событие  . Аналогично сумма
. Аналогично сумма 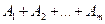 произвольного количества событий
произвольного количества событий  состоит из всех элементарных событий, которые входят, по меньшей мере, в одно из событий
состоит из всех элементарных событий, которые входят, по меньшей мере, в одно из событий  . Приведем еще один пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие
. Приведем еще один пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие 
 означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.
означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков. .[1] Событие
.[1] Событие  Разностью событий
Разностью событий  , состоящее из всех исходов события
, состоящее из всех исходов события  .
. Событие
Событие  . В случае строго включения, имеем
. В случае строго включения, имеем 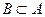 . В этом случае говорят, что событие
. В этом случае говорят, что событие  ,
,  .
. ,
, 
 означает, что условие выполняется для любого
означает, что условие выполняется для любого  , отличного от
, отличного от  . В результате эксперимента обязательно произойдет одно и только одно из событий, составляющих полную группу. Любое событие вместе со своим дополнением образует полную группу событий. В частности всевозможные элементарные события по отдельности образуют полную группу событий. События
. В результате эксперимента обязательно произойдет одно и только одно из событий, составляющих полную группу. Любое событие вместе со своим дополнением образует полную группу событий. В частности всевозможные элементарные события по отдельности образуют полную группу событий. События  ,
, 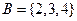 и
и  также образуют полную группу событий для эксперимента подбрасывания игральной кости.
также образуют полную группу событий для эксперимента подбрасывания игральной кости.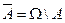 ,
,  .
.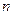 числа элементарных событий и все элементарные события равновозможны, т.е. ни одному из них из них нельзя отдать предпочтения до испытания(имеет место принцип симетричности). Если
числа элементарных событий и все элементарные события равновозможны, т.е. ни одному из них из них нельзя отдать предпочтения до испытания(имеет место принцип симетричности). Если 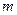 из них принадлежат событию A, то вероятностью события A называется число
из них принадлежат событию A, то вероятностью события A называется число (1)
(1) , и
, и  ,
, 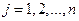 ,
,  , то
, то  . Очевидно, что
. Очевидно, что  .
. , где через
, где через  обозначена вероятность выпадения числа 3.
обозначена вероятность выпадения числа 3. , где через
, где через  (каждое значение выпавшей грани на первой кости может сочетаться с любым значением на второй кости). Из этих 36 исходов событию A будут благоприятствовать исходы: (1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1) [3], т.е. всего 6 (m = 6). По формуле имеем:
(каждое значение выпавшей грани на первой кости может сочетаться с любым значением на второй кости). Из этих 36 исходов событию A будут благоприятствовать исходы: (1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1) [3], т.е. всего 6 (m = 6). По формуле имеем: 
 . Следовательно, событие получить в сумме 7 очков – более вероятное событие, чем получить 8.
. Следовательно, событие получить в сумме 7 очков – более вероятное событие, чем получить 8.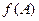 появления события
появления события 


