
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Односторонние и двухсторонние значения вероятностейСодержание книги
Поиск на нашем сайте
При известном законе распределения с.в. часто приходится решать задачи трех стандартных типов: · найти вероятность того, что случайная величина X окажется равной (не равной) некоторому значению · найти вероятность того, что случайная величина X окажется больше (меньше) некоторого значения · найти вероятность того, что случайная величина X окажется не меньше Первую вероятность называют "точечной", ее можно найти из закона распределения, но только для дискретной случайной величины. Разумеется, что вероятность равенства задана самим законом распределения, а вероятность неравенства составляет Нормальное распределение В 1910 году при изучении нескольких тысяч американцев по величине роста была обнаружена интересная закономерность в распределении этого показателя, которая заключалась в более или менее симметричном накоплении значений в центре ряда варьирования и постепенное убывание по численности по мере удаления от центра. Как выяснилось, такая закономерность присуща многим с.в., значения которых обусловлены достаточно большим количеством примерно одинаковых по силе воздействия случайных факторов (причин). Закон распределения таких с.в. получил название нормального закона распределения. Для нормального закона функция распределения определяется как
где
- функция плотности. Таким образом, закон нормального распределения является параметрическим и зависит от двух параметров Чаще всего закон нормального распределения используется для нормированной случайной величины
Площадь под кривой на заданном интервале
попадания в этот интервал. В условиях стандартного закона распределения можно отметить следующие особенности: · Доказано, что целый ряд “классических” (хорошо изученных и часто используемых при статистических вычислениях) распределений (как дискретных, так и непрерывных) стремятся к нормальному при непрерывном изменении их внутренних параметров. Поэтому нормальное распределение используется для аппроксимации различных распределений, которые возникают при анализе достаточно большого объема данных. · Симметрия нормального распределения позволяет достаточно просто оценивать вероятность попадания значений случайной нормированной величины в заданный диапазон. · Очень часто в прикладной статистике приходится использовать понятие “маловероятного” значения. Для нормированной величины с нормальным распределением вероятность попадания в диапазон ± 3 составляет 0.9973 (правило “трех сигм”), следовательно, принятие значения случайной величиной за пределами этого диапазона является маловероятным событием. · Особую роль нормальное распределение играет при решении вопросов о “представительности” наблюдений. Оказывается, что работа с выборочными распределениями в большинстве случаев позволяет решить проблему оценки предварительных выводов, предположений, гипотез – с использованием разработанных и теоретически обоснованных приемов на базе нормального закона. Нормальное распределение является важным по многим причинам. В условиях, когда наблюдаемый процесс зависит от большого числа взаимо-независимых (или слабозависимых) факторов, вклад каждого из которых в процесс очень мал, распределение вероятностей такого процесса описывается нормальным законом. Характерное свойство нормального распределения состоит в том, что 68% всех его наблюдений лежат в диапазоне ±1 стандартное отклонение от среднего, а диапазон ±2 стандартных отклонения содержит 95% значений. Другими словами, при нормальном распределении, стандартизованные наблюдения, меньшие -2 или большие +2, имеют относительную частоту менее 5%.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.45.223 (0.006 с.) |

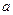 ?
? ?
?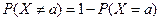 . Вторую вероятность принято называть "односторонней". Вычислять ее также достаточно просто – как сумму вероятностей всех допустимых значений больших(меньших)
. Вторую вероятность принято называть "односторонней". Вычислять ее также достаточно просто – как сумму вероятностей всех допустимых значений больших(меньших)  ,
, - математическое ожидание, а
- математическое ожидание, а  - средне квадратичное отклонение с.в., а
- средне квадратичное отклонение с.в., а

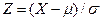 , у которой
, у которой  и
и  . Закон распределения нормированной нормальной случайной величины называется стандартным, его функция распределения обозначается через
. Закон распределения нормированной нормальной случайной величины называется стандартным, его функция распределения обозначается через  . Табличные значения приводятся для
. Табличные значения приводятся для 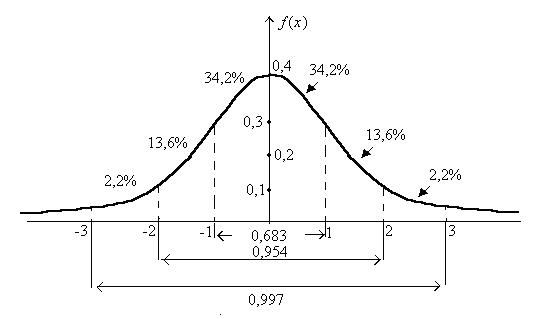
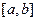 определяет вероятность
определяет вероятность



